磨粒簇叶序砂轮磨削结构化表面形貌仿真

李兴山，汪宇晨，吕玉山，宋 征，陶思远

(1.沈阳理工大学 机械工程学院，沈阳 110159；2.辽宁电力中心医院，沈阳 110015)

在机械制造中，人们利用仿生结构化表面技术来达到减阻耐磨效果，这对零部件性能的提升有重要意义。目前，在结构化表面磨削领域，主要采用结构化修整砂轮和成形砂轮磨削的方式。文献[1-2]制备了双螺旋槽砂轮，用其磨削工件平面，获得了沟槽状结构化表面，成功将砂轮表面纹理复制到工件表面上而获得规则表面纹理。文献[3]设计了砂轮表面结构化修整系统，能够在砂轮表面上修整形成所需纹理图案。BerendDenkena等[4]采用微沟槽结构化砂轮磨削加工出V形槽非光滑表面的气压机叶片，可采用磨削的方式在金属表面直接获得沟槽结构。谢晋等[5]提出采用精密磨削和微细磨削组合加工工艺，在陶瓷飞行体表面加工出曲面微沟槽结构，以减小飞行阻力和增强雷达散射。上述研究成果对推动结构化表面磨削有重要的理论意义和应用价值。本文从磨削几何学理论出发，根据不同的结构化表面特征，采用叶序排布原理设计磨粒簇叶序排布砂轮，并对磨粒簇砂轮磨削平面减阻表面进行仿真，通过仿真来比较各参数对结构化表面形貌的影响规律。

1 砂轮磨削运动学分析

1.1 砂轮运动轨迹方程的建立

图1为砂轮磨削平面工件运动示意图，分别建立砂轮坐标系(OsXsYsZs)、工件坐标系(OwXwYwZw)、砂轮旋转坐标系(O′sX′sY′sZ′s)和工件进给坐标系(O′wX′wY′wZ′w)，砂轮到工件中心的距离为m，旋转速度为Vs。

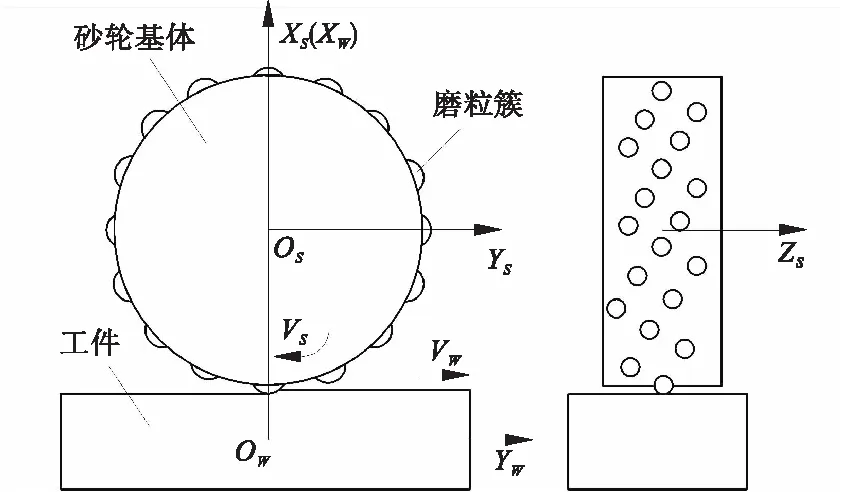
图1 砂轮磨削平面工件运动示意图

通过坐标系之间的转换可以获得不同坐标系之间的运动关系，定义转换矩阵Mmn表示从坐标系OnXnYnZn到OmXmYmZm的坐标变换，根据运动关系得到坐标转换矩阵Mww′、Mw′s以及Ms′s；定义向量U为磨粒的位置向量，则根据运动关系建立如下的坐标变换矩阵。

(1)

(2)

(3)

(4)

通过三次坐标变换得到砂轮上任何一个磨粒簇相对于工件坐标系的轨迹矩阵J为

J=[Mww′][Mw′s][Ms′s][U]

(5)

1.2 磨粒运动轨迹干涉的条件

为实现磨削出规则的结构化表面，需要推导出砂轮的转速与工件进给的关系，只有保证相互的运动学条件，才能实现磨削的痕迹规则排布[6]。本仿真采用球冠型、矩形及锥形磨粒簇，在砂轮上叶序排布。砂轮磨削过程中，砂轮上磨粒簇做圆周运动，工件做直线运动，采用逆磨方式，如图2所示。

图2 磨粒簇砂轮磨削示意图

图2中，ap为磨削深度；L为单颗磨粒磨削工件水平方向上的磨削距离。设砂轮逆磨时，砂轮半径为Rs，转速为n，工件的进给速度为Vw。则两个凹坑间距离L0为

L0=vwts

(6)

(7)

式中：θ为砂轮上相邻两个磨粒簇间的角度；ts为砂轮磨粒磨削一个凹坑的时间。将式(7)代入式(6)，得

(8)

对于特定磨粒簇形状，干涉条件有所变化，以球冠状磨粒簇为例。设砂轮逆磨时，砂轮半径为Rs，球冠半径为Rt，球冠突出部分高为e，则球冠状磨粒簇从一点切入到另一点切出的轨迹为摆线，其在水平方向的磨削距离为

vwt1

(9)

式中t1为砂轮球冠磨粒簇切入切出的时间。

(10)

(11)

通过L与L0的不同比值，即可获得不同特征的结构化表面。

2 结构化表面形貌仿真

2.1 仿真策略与基本条件

结构化表面形貌取决于磨粒簇砂轮的表面形貌和磨削参数。用Matlab软件仿真，初始参数：砂轮半径Rs=47.5mm，砂轮转速n=3000r/min，球冠形磨粒簇直径Rm=1.5mm，矩形磨粒簇高为1.5mm；锥形磨粒簇高度为1.5mm；工件材质为45号钢。仿真系统会根据运动方程获得磨粒簇相对于工件的运动轨迹，完成磨削后工件表面的创建[7]。

2.2 仿真结果与分析

2.2.1 形成凹坑的结构化表面

设定参数为：球冠形磨粒簇球冠半径Rt∈[25mm,45mm]，矩形磨粒簇宽度b∈[1mm,2mm]，锥角θ∈[100°,120°]，叶序系数h∈[0.13mm,0.2mm]，磨削深度ap∈[0.01mm,0.03mm]，工件的进给速度Vw=300mm/s。图3所示为形状不同的磨粒簇形成的凹坑结构化表面。

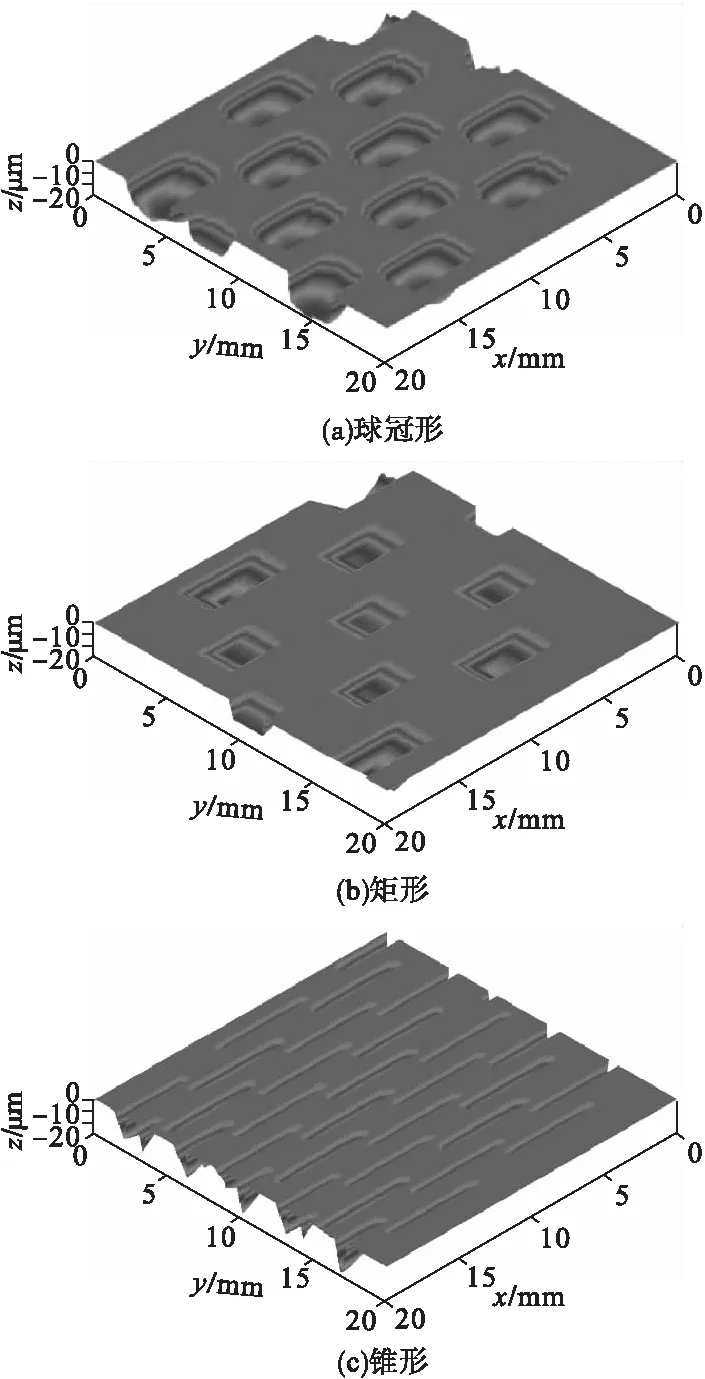
图3 凹坑结构化表面

通过仿真可得，球冠形磨粒簇砂轮可磨削出椭圆形凹坑，矩形磨粒簇砂轮可磨削出矩形凹坑，锥形磨粒簇砂轮可磨削出菱形的凹坑。球冠形磨粒簇砂轮的球冠半径增大，凹坑的宽度也随之增大；矩形磨粒簇的矩形越宽，磨削出的凹坑的宽度也越大；锥形磨粒簇砂轮的锥角越大，凹坑的宽度也越大。随着叶序系数h的增加，凹坑间纵向距离逐渐增大，凹坑分布疏远。随着磨削深度ap的增大，凹坑深度也逐渐加深，凹坑的宽度也越大。

2.2.2 形成凸台的结构化表面

设定工件的进给速度为Vw=120mm/min，球冠形磨粒簇叶序系数hb∈[0.2mm,0.25mm]，矩形磨粒簇叶序系数hr∈[0.15mm,0.2mm]，锥形磨粒簇叶序系数hc∈[0.03mm,0.1mm]，其他参数不变。图4所示为形状不同的磨粒簇形成的凸台结构化表面。

图4 凸台结构化表面

球冠形磨粒簇砂轮可以磨削出四边均为凹边矩形凸台；矩形磨粒簇砂轮可以磨削出矩形凸台；锥形磨粒簇可以磨削出长条状凸台。当叶序系数h减小，凹坑的纵向距离也逐渐缩短，工件的凹坑也逐渐密集，直到凹坑周围四个凹坑相交，形成凸台结构化表面。

2.2.3 形成沟槽的结构化表面

设定工件的进给速度为Vw∈[30mm/s,300mm/s]，球冠形磨粒簇叶序系数hb=0.8mm，矩形磨粒簇叶序系数hr=1mm，锥形磨粒簇叶序系数hc=0.5mm，其他参数不变。图5所示为形状不同的磨粒簇形成的沟槽结构化表面。

球冠形磨粒簇砂轮磨削出的沟槽表面截面为圆弧形；矩形磨粒簇砂轮磨削出的沟槽表面截面为矩形；锥形磨粒簇砂轮磨削出的沟槽表面截面为三角形。随着工件进给速度的减小，凹坑长度也逐渐减小，相邻凹坑间的距离也逐渐缩短，直到出现多个相邻凹坑重合相连的现象，形成了沟槽结构化表面。

图5 沟槽结构化表面

3 结论

基于磨粒簇叶序砂轮的数学模型，建立了磨粒的运动方程并研究了实现结构化表面的磨削条件。利用Matlab仿真了不同形状磨粒簇在工件表面产生的结构化表面的形貌特征，模拟了磨粒簇砂轮磨削结构化表面的过程，仿真得到相应的结构化表面，证明了该方案的可行性。

通过仿真结果对比，得到不同排布参数和磨削参数对结构化表面形貌产生的影响；叶序砂轮上的磨粒簇形状不同，可得到的不同形状的结构化表面；磨粒簇结构化砂轮的磨削深度越大，凹坑深度越深，凹坑的宽度越长。