基于K观测器的高平机电液系统动态面控制

杨善平,尹 强,羊 柳

(南京理工大学 机械工程学院，南京 210094)

高平机是火炮武器系统的关键部件，其作用是驱动起落部分绕耳轴做俯仰运动至期望射角[1-2]。其位置控制精度的高低将直接影响到火力打击的准确性[3]。高平机以液压为驱动力，是一个典型的电液伺服系统。同时，高平机电液系统是一个典型的非线性非匹配系统。建立其精确的数学模型有一定的难度，而且使用PID等线性控制很难达到满意的效果。由于滑模控制算法具有设计简单、抗干扰能力较强的特点，使其在电液控制领域的得到广泛应用[4-6]。然而滑模控制不能解决非匹配问题[7]，必须结合鲁棒控制、backstepping理论等方法。文献[8]采用动态面自适应控制策略，有效解决了液压起竖系统非线性以及参数不确定性等问题，仿真结果表明动态面自适应控制具有较好的跟踪性能。受此启发，本文提出了一种基于K观测器的某火炮高平机电液系统动态面控制策略(KDSSMC)，设计了自适应控制律实时估计状态方程中的未知参数，最后通过联合仿真的方法验证了所提出的控制策略具有良好的动态跟踪性能及较小的问题误差。

1 高平机电液系统非线性模型

高平机电液系统结构如图1所示，其主要由高平机油缸、身管、耳轴、伺服阀、液压油源等组成。其中高平机油缸(后文简称油缸)为三腔并联式结构，A、B两腔活塞面积相等，C腔与蓄能器相连起到平衡部分重力的作用，由于其并非传统的两腔式油缸，内部结构相对复杂，很难使用AMEsim中的标准液压库进行建模。为使建模方便，将其作用力等效为对称缸作用力和一与油缸位移相关作用力的矢量“叠加”。控制器输出电压信号的大小，控制伺服阀阀口的开度，进而控制油缸的伸缩及速度。图1中，坐标原点O为油缸下铰点，O1为身管回转点，O2为油缸上铰点。l为身管重心到身管回转点的距离，l1为零射角时高平机油缸的初始安装距，l2为耳轴距高平机油缸前支点的距离，l3为耳轴距离高平机油缸后支点的距离，θ为身管当前角度。

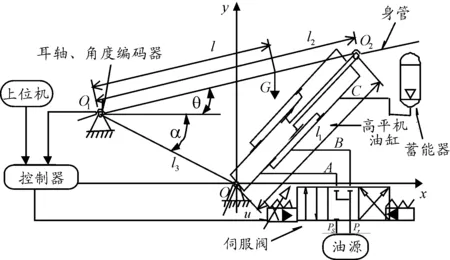
图1 高平机电液系统结构示意图

(1)

式(1)中:cd为伺服阀阀口流量系数；w为伺服阀节流窗口面积梯度；ρ为油液密度；Ps为系统供油压力；PL为负载压力；xv为伺服阀阀芯位移，由于伺服阀的固有频率远远大于系统的固有频率，故伺服阀的阀芯位移xv与输入到伺服阀放大器的控制电压u可等效为比例环节，即xv=Kxu。

根据流量连续性方程，得：

(2)

式(2)中:A为活塞有效作用面积；x为油缸位移；Ct为总泄露系数；V1=V01+Ax为A腔(含与伺服阀相连接的管路部分)工作容积；V2=V02-Ax为B腔(含与伺服阀相连接的管路部分)工作容积；βe为油液体积弹性模量。

设油缸总的容积为Vt，即Vt=V1+V2，将式(2)中两式合并得

由牛顿第二定律得：

(3)

式(3)中:mt为油缸等效质量；x为活塞杆的位移；B为活塞的粘性阻尼系数；K为负载弹簧刚度，由于本系统中负载主要是惯性负载，所以设其为0；F为外负载。

由波义尔气体定律可推得

(4)

式(4)中：Fc为C腔平衡力；P0为蓄能器初始气压；Ac为C腔有效作用面积；V0为蓄能器初始容积；n为气体多变指数，这里取1.25。

(5)

式(5)中：F为负载力；J为系统转动惯量；B为油缸活塞和负载的粘性阻尼系数；Td为系统不平衡力矩即外部扰动和未建模特性的综合作用。

可以证明油缸作用力的力臂为

(6)

式(6)中，

2 基于K观测器的动态面控制

2.1 状态空间描述变换

为减少传感器的数量，将式(6)进行变换，使其第三个式子中不含θ2和θ3，仅使用角度反馈便可实现对身管位置的控制。将d(t)简化为β6cosθ1，其中β6为未知参数。

由式(6)可得

D2y=β1θ3-β2θ2-β6cosθ1

(7)

式(7)中，Dn表示dn/dt。于是

(8)

对式(8)求导得

于是

D3y+(β2+β3)D2y+(β2β3+β1β4)Dy+β6cosy=

-β3β6cosy+β1β5u

(9)

式(9)中，a1=β2+β3，a2=β2β3+β1β4，a3=β3，a4=-β3β6，d0=β1β5。

定义：z1=y,z2=Dy,z3=D2y+a1Dy+a2y+a3cosy，则系统的状态方程可转化为

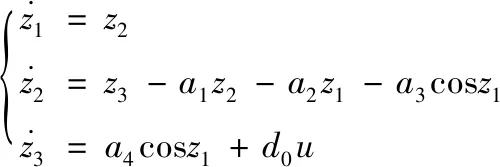
利用z1作为系统反馈量，并通过K观测器求出状态z=[z1,z2,z3]T，然后通过设计控制律u以使系统输出z1跟踪z1d，从而实现基于信号θ1的跟踪。

2.2 K观测器设计

参照非线性状态方程形式，将系统状态方程改写为

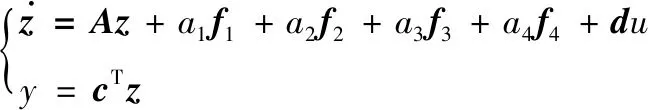
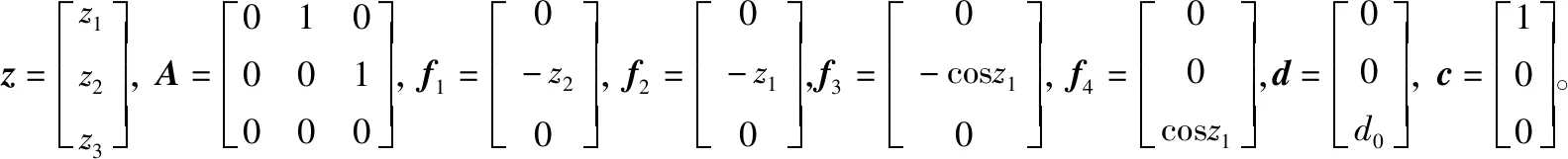
设计如下K观测器

(10)

式(10)中，α,δ1,δ2,δ3,δ4,v均为观测器状态向量，k=[k1k2k3]T，e3=[0 0 1]T，v=[v1v2v3]T。

由于

由于A0满足Hurwitz，求其特征值，令|λI-A0|=0得

λ3+k1λ2+k2λ+k3=0

取极点为-a,则(λ+a)3=0，于是k1=3a,k2=3a2,k3=a3。

于是

由此得K观测器状态估计量

a3(A0δ3+f3)+a4(A0δ4+f4)+d0(A0v+e3u)=

由于bu=d0e3u,kcTz=ky=kz1，于是

2.3 控制器设计

根据K观测器重构系统的未知状态，实现对火炮身管的角度位置跟踪，并避免微分爆炸现象，采用一阶低通滤波器计算虚拟控制的导数，可以简化控制器的设计，并有效减少控制器的求解时间。

第1步，定义系统第一个误差子系统，

e1=z1-z1d

(11)

式(11)中：z1为实际角度；z1d为期望角度。对e1求导得

定义

(12)

式(12)中，l1为大于零的常数。

设计虚拟控制

(13)

取参数估计值的自适应律为

(14)

式(14)中：Q为正定对称矩阵；η为大于零的常数。

(15)

第2步，定义第2个误差子系统：

e2=v2-v2d

(16)

对式(16)求导得：

设计虚拟控制

(17)

(18)

第3步，定义第3个误差子系统：

e3=v3-v3d

(19)

对式(19)求导得：

于是，最终得到控制律：

(20)

式(20)中，l3为大于零的常数。

2.4 稳定性证明

首先定义边界层误差

(21)

由式(15)、式(18)和式(21)可得：

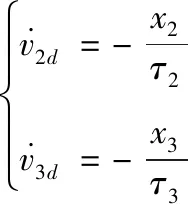
然后定义参数估计误差：

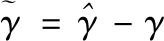
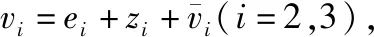
对边界层误差求导得：

存在连续非负函数Bi(i=2,3)满足

(22)

由式(22)可推得：

定义Lyapunov函数

V=V1+V2+V3

(23)

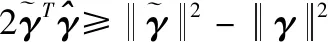
(24)

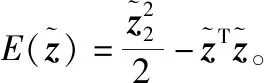
其中σ为正常数。故

(25)

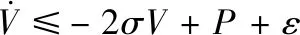
解之得

于是

故整个控制器是渐趋稳定的。

3 仿真分析与验证

根据高平机电液系统组成及工作原理，结合键合图理论，搭建了高平机电液系统AMESim模型，如图2所示。

1.电机；2.齿轮泵；3.溢流阀；4.油箱；5.伺服阀；6.角度传感器；7.旋转铰；8.三端口实体；9.复合驱动铰；10.双向平衡阀；11.高平机油缸；12.位移传感器

图2 高平机电液系统AMESim模型示意图

使用Matlab中的S-function模块编写控制程序，并设计与AMEsim联合仿真的接口，经调试得到联合仿真参数k=[k1k2k3]T=[0.36 0.04 0.001]T，l1=0.000 14，l2=0.005，l3=0.03，τ2=τ3=0.01，Q=diag[0.000 01 0.78 2 0.51 0.000 078]，η=0.1。最终得到联合仿真的结果分别如图3～图7所示。

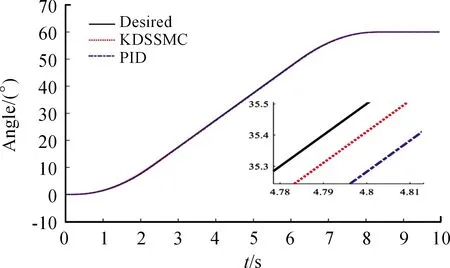
图3 角度跟踪曲线

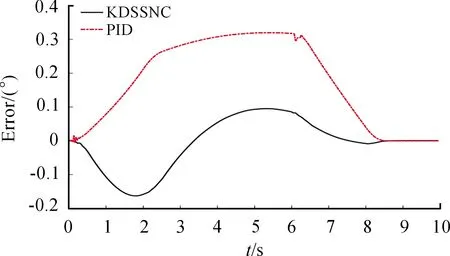
图4 角度跟踪误差曲线

图5 控制器输出

图6 γ1、γ3和γ5的估计值曲线

由图3和图4可知：所设计控制器的最大动态跟踪误差约为0.18°，最大稳态误差约为0.03°，整个跟踪过程平稳，无明显冲击。与PID控制相比，最大动态跟踪误差下降约0.18°，最大稳态误差下降约0.05°。所设计的控制器仅使用角度传感器即可达到输出反馈控制的目的，而且引入滤波器有效解决了微分膨胀问题。由图5可知：控制器的输出信号曲线圆滑，无高频抖动。由图6和图7可知：所设计的自适应律可以根据系统外部扰动，实时调整未知参数值的大小，并且各未知参数的估计值均为有界的，这也证明了所设计控制器具有较高的鲁棒性。

图7 γ2和γ4的估计值曲线

4 结论

1) 建立了某火炮高平机电液系统的非线性数学模型，通过状态方程等效变换的方法，将系统状态方程等效转化，仅使用角度传感器便可得到系统状态方程所有的状态变量。

2) 针对火炮高平机电液系统存在非线性非匹配的特点提出了一种基于K观测器的动态面控制策略，引入反演方法有效解决了非匹配问题，通过所设计的自适应律估计出系统状态方程的未知参数，使用联合仿真的方法验证了所提出的控制策略具有较好的动态跟踪性能及较高的鲁棒性。