尾翼弹高低空气动特性仿真及外弹道计算

岳 通，王惠源，张成卿

(中北大学 机电工程学院，太原 030051)

弹箭气动参数对气动外形设计及弹道的计算具有重要意义，为此众多学者对弹箭气动参数的计算进行了大量的研究。文献[1]研究了大长径比超音速卷弧尾翼火箭弹在标准气象条件下,卷弧尾翼对全弹气动特性的影响；文献[2]通过研究得到某35 mm超音速榴弹在标准气象条件下阻力系数随弹形的变化规律；文献[3]研究了在标准气象条件下，某型导弹的亚音速气动特性并给出了该弹的气动参数；文献[4]研究了某小型单兵巡飞弹在2.5 km海拔高度处的气动参数，为巡飞弹的气动外形的设计提供参考；文献[5]研究了 4 km高空条件下，有无弹带对高速旋转弹丸气动特性的影响，得到弹带使得阻力系数有一定的升高，但弹带形状对弹丸升力系数影响不大的相关结论；文献[6]采用计算流体动力学对M910弹丸在全音速范围内静压为101 325 Pa,静温为 288 K条件下的气动特性进行了模拟，得到各气动参数与实验数据的误差在10%以内，具有较高的计算精度。文献[7]分析得到了某旋转弹丸在全音速范围内，静压为101 325 Pa,静温为292 K条件下，静态空气动力系数与大多数动力导数具有很好的一致性。文献[8]对来流马赫数Ma=0.7～2.7，攻角为 0°情况下的旋转弹丸绕流场进行了数值模拟,所得阻力系数结果与实验值和半经验公式计算值符合较好。文献[9]通过运用牛顿撞击理论计算得到某高超声速制导炮弹在静压为101 325 Pa，静温为293 K条件下的阻力系数与实验结果吻合较好。因此,该计算方法能够可靠地获得高超声速制导炮弹的气动力特性。文献[10]采用CFD方法，基于SST湍流模型对超声速火箭弹在特定海拔高度下的外流场进行了计算，计算结果表明该数值方法能较好地计算气动力参数。

然而在以往对弹箭气动参数的研究中，国内外很多学者只研究了固定气象条件下，弹箭的气动参数。少有人研究弹箭气动参数随不同海拔高度处的变化规律，但是由于不同海拔高度处的气象参数变化较大，则在不同海拔处发射的弹箭在飞行过程中受到的气动力也将会有较大的变化，从而影响弹箭的弹道。因此本文以小口径尾翼弹为研究对象，研究该尾翼弹随不同海拔高度，不同马赫数处的气动特性及其外弹道特性的变化规律，为小口径尾翼弹在不同海拔高度处的应用奠定基础。

1 数值计算方法

本文研究海拔高度在20 km以内，小口径尾翼弹的气动特性，其所属流域为连续流域，气体的间断效应并不显著，连续性假设成立，所以仍可运Navier-Stokes方程进行计算，选用雷诺平均的N-S方程作为控制方程。

控制方程为[11]：

式中：U为解向量；F和G为通量向量；Ma∞为来流马赫数；γ为比热比，Re∞为来流雷诺数。

湍流模型采用涡黏模型中的Shear-Stress Transport(SST)k-ω模型，求解2个方程的输运方程，即湍动能k,湍流频率ω，SSTk-ω模型考虑到了湍流剪切应力的输运，能较好的模拟弹箭的气动力，因此选用该湍流模型计算尾翼弹的气动参数，k和ω的输运方程具体形式为[12]：

尾翼弹外形参数如图1所示。

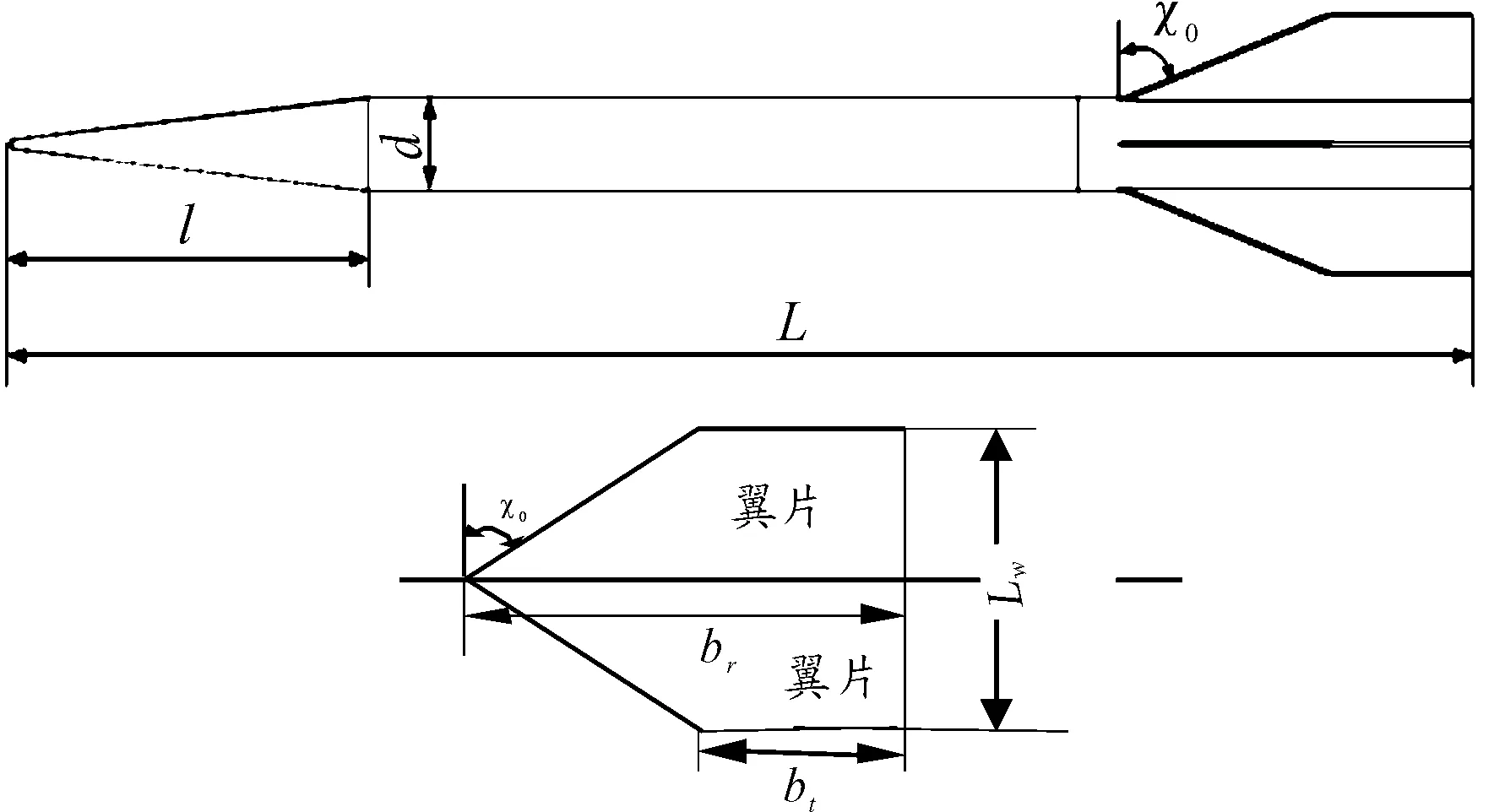
图1 尾翼弹外形参数

综合考虑计算精度与计算效率，将计算域分层，在大的圆柱外流域内再增加一个小圆柱加密区域[13]，大圆柱形外流域直径为18倍弹径长度为10倍弹长，小圆柱流域直径为5倍弹径，长度为3倍弹长。采用求解黏性子层的方法对近壁面区域进行计算，即需要保证y+<5使得第一层网格节点位于粘性子层内[14]，并保证边界层数为8，划分得到如图2和图3所示的多面体网格。

图2 计算域网格

图3 弹体表面网格

由美国1976年标准大气分段逼近公式[15]计算：

计算位势高度H,它与几何高度Z的关系为：

H=Z/(1+Z/R0)

式中：R0=6356.766 km,为地球平均半径；Z单位为 km。

1) 当0≤Z≤11.019 km时：

p/p0=W5.252 9,ρ/ρ0=W4.255 9

2) 当11.0191 km≤Z≤20.063 1 km时：

p/p0=0.119 53W，ρ/ρ0=0.158 98W

式中：p0=1 013.25 hPa，密度ρ0=1.225 kg/m3。

3) 黏性系数随高度变化的计算公式：

式中：βa=1.458×10-6kg/(s·m·K1/2)，Ts=110.4 K。

式中：k为绝热指数，空气k=1.4;Rg为气体常数，空气Rg=287 J/(kg·K)；T为热力学温度(K)。

由以上公式计算得到各海拔高度的气象参数值，作出相关曲线如图4所示。

图4 气象参数变化曲线

设置流场外壁面为压力远场边界，弹体表面采用无滑移壁面边界条件，求解方法采用压力-速度耦合(Coupled)算法，对流通量采用二阶迎风格式进行离散。对气动参数计算时，远场的温度、压力、密度、黏性系数等气象参数已由以上部分计算得到。假设来流为理想气体，来流马赫数为Ma=0.6～3，攻角为α=0°。

算法有效性验证：

本文选用标准模型(Non-Rolling Basic Finner)进行数值算法有效性验证，该标准模型已由美军弹道研究实验室进行了大量风洞试验。图5为其几何外形参数，弹体直径d=20 mm，以弹体横截面积为参考面积,并用以上数值方法模拟标模弹的外流场，得到零升阻力系数，然后作出图6。

图5 标准模型

图6 标模弹零升阻力系数曲线

图6所示的仿真零升阻力系数曲线和文献[16]的实验值拟合曲线大致吻合，误差小于10%，在允许范围以内。由此可知，本文中所用的数值计算方法具有较高的可信度。

2 计算结果与分析

由数值方法计算得到不同海拔高度处的尾翼弹阻力值，作出图7：在同一马赫数下，尾翼弹阻力随着海拔高度的增加在减小，同一海拔高度处，尾翼弹阻力随着马赫数的增加近似线性增加。

模糊控制、专家控制、神经网络控制、PID控制、自适应控制等是工业机器人运动控制系统的主要方法，为了达到更好的动态性能，最终实现控制要求，一些新的控制方法就出现了。在控制算法方面既要保证一定的鲁棒性，又要满足参数实时变化的要求。

图7 尾翼弹阻力随海拔高度的变化曲线

图8 阻力系数随海拔高度的变化曲线

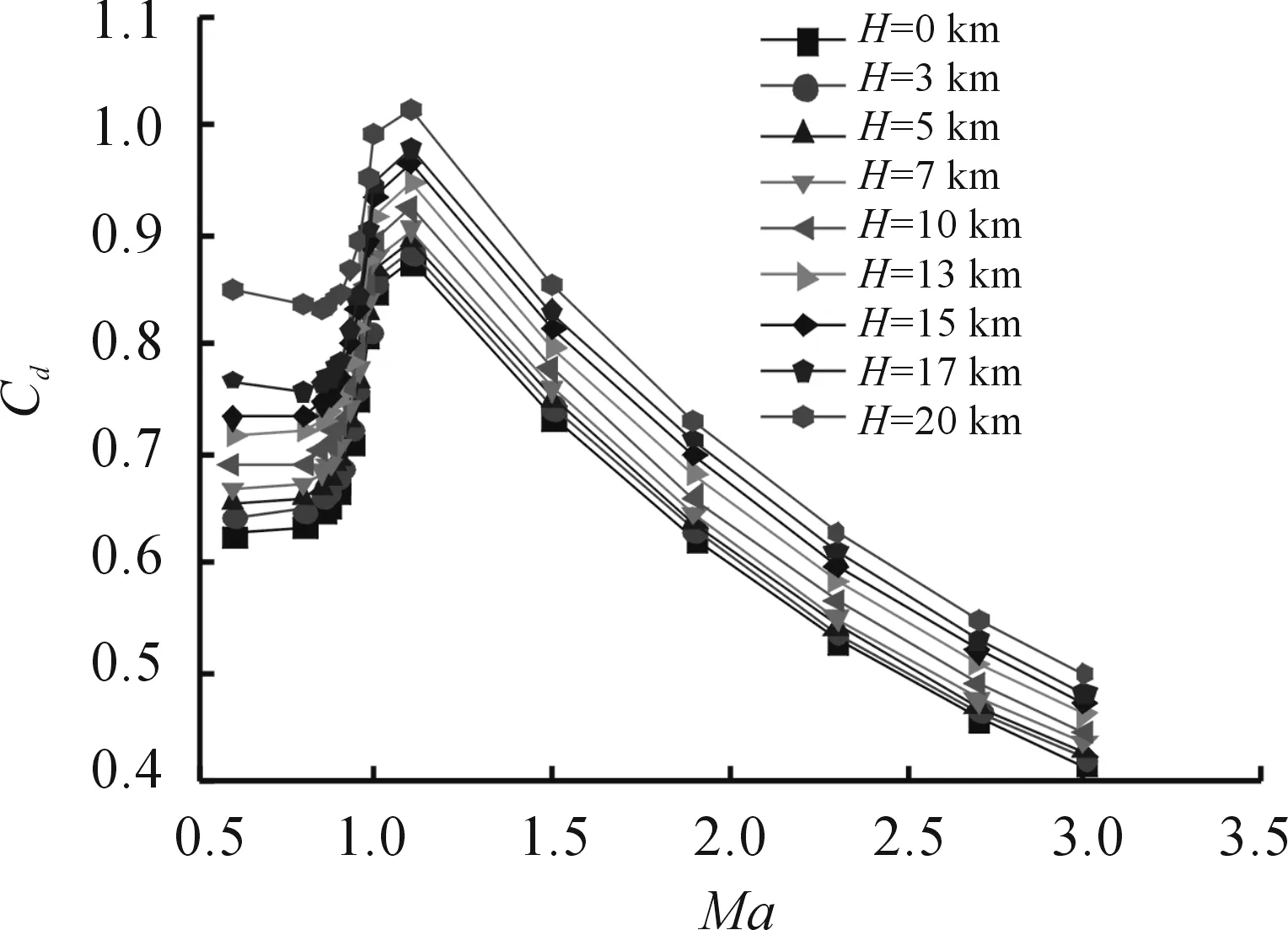
图9 阻力系数随马赫数的变化曲线

在Ma=0.6到Ma=3全声速范围内，阻力系数随着海拔高度的升高而增加，在同一海拔高度处，阻力系数随着马赫数的变化趋势相同。

由数值方法计算得到弹体各部分阻力系数变化值，作出图11所示曲线，并可以得到：随着海拔高度的增加，尾翼弹头部，弹体部，尾翼部的阻力系数都随着海拔高度的增加而增加，其中尾翼部的阻力系数对海拔高度最为敏感，而弹底阻力系数随海拔高度增加而降低。因此尾翼部的阻力系数升高是造成阻力系数随着高度增加的主要原因。

图10 不同海拔高度处的速度云图

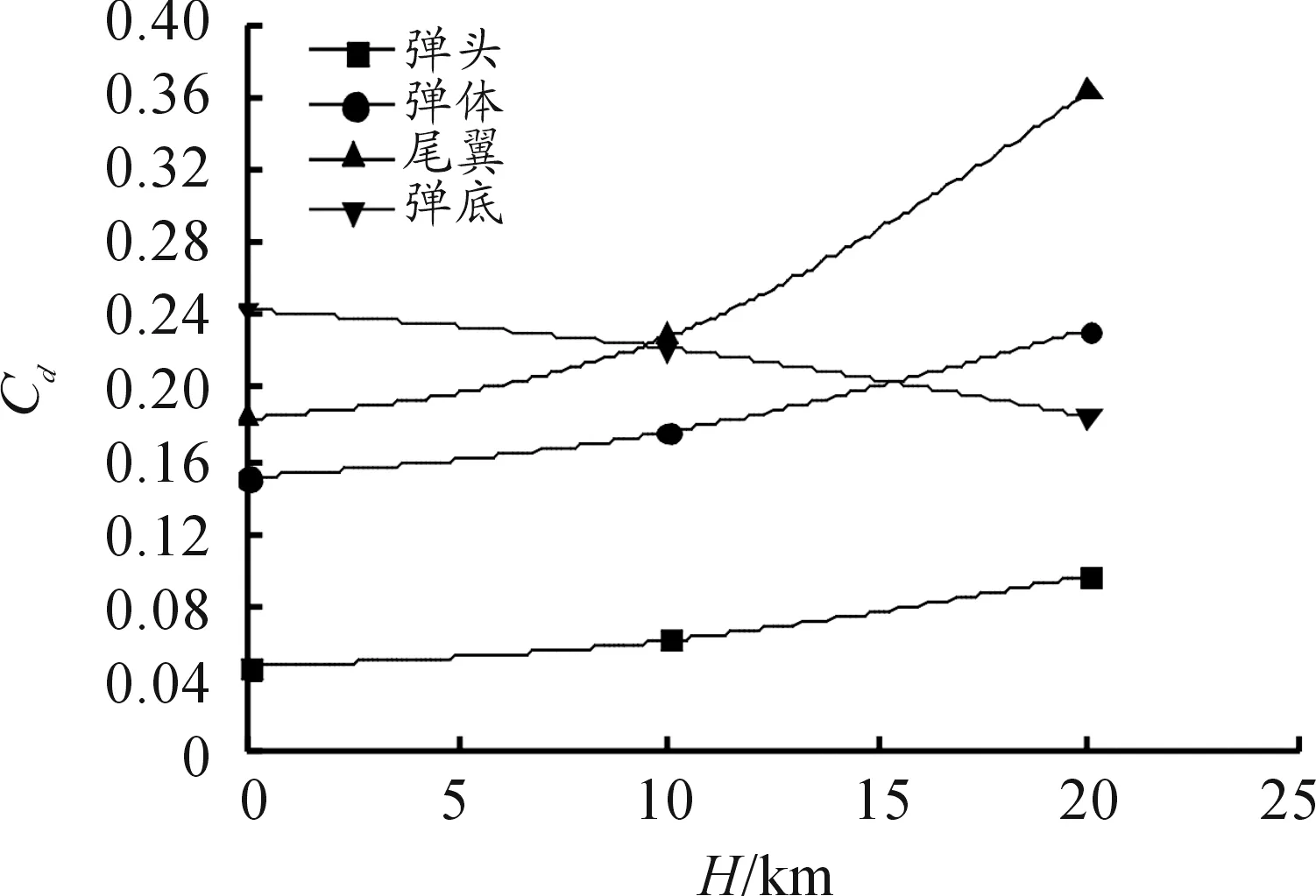
图11 Ma=0.6时弹体各部分的阻力系数变化曲线

从图8曲线得到：在海拔高度17 km内，阻力系数与海拔高度基本为线性关系；亚音速范围内的阻力系数增加速率要高于超音速范围的增加速率；在海拔高度超过17 km后，亚音速段，跨音速段的阻力系数增加较快，而超音速段的增长速率基本不变，亚音速段，跨音速段的阻力系数对海拔高度的变化更为灵敏。

3 阻力系数拟合

文献[17]提出：用Logistic曲线与三次抛物线分俩段拟合亚音速段(1.1Ma为界)，超音速段弹丸阻力系数，该方法拟合误差较低且分段数较少，方便于外弹道编程使用。

拟合亚音速段Logistic曲线解析表达式为：

式中：a分别为Logistic曲线下渐进线纵坐标值；b为上下两条平行的渐进线之间的距离；c，d为拟合曲线待定系数；x为弹丸飞行马赫数；y为弹丸零升阻力系数。

拟合超音速段三次抛物曲线解析表达式为：

y=Ax3+Bx2+Cx+D

式中：x为弹丸飞行马赫数；y为弹丸零升阻力系数；A、B、C、D为拟合曲线待定系数。

用确定系数R-square来表征拟合的程度：

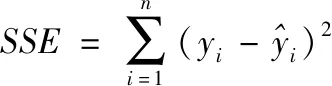
由上式可知R-square越接近1，表明所拟合方程的拟合程度高。用Matlab拟合方程R-square值均为0.99以上，拟合各海拔高度处阻力系数方程如表1，拟合曲线如图12。

图12 海拔0 km、10 km、20 km处拟合方程曲线

表1 各海拔高度处阻力系数拟合方程

4 外弹道计算

射角θ0=10°；初速v0=900m/s；t=0,x=0；y=0km,10km,17km; vx=vvcosθ0；vy=v0sinθ0

由质点外弹道计算得到各海拔高度处发射该尾翼弹的外弹道特性曲线，质点外弹道方程组[18]：

由质点外弹道方程计算得到弹道高，弹丸存速，弹道倾角随海拔高度的变化值，作出图13。

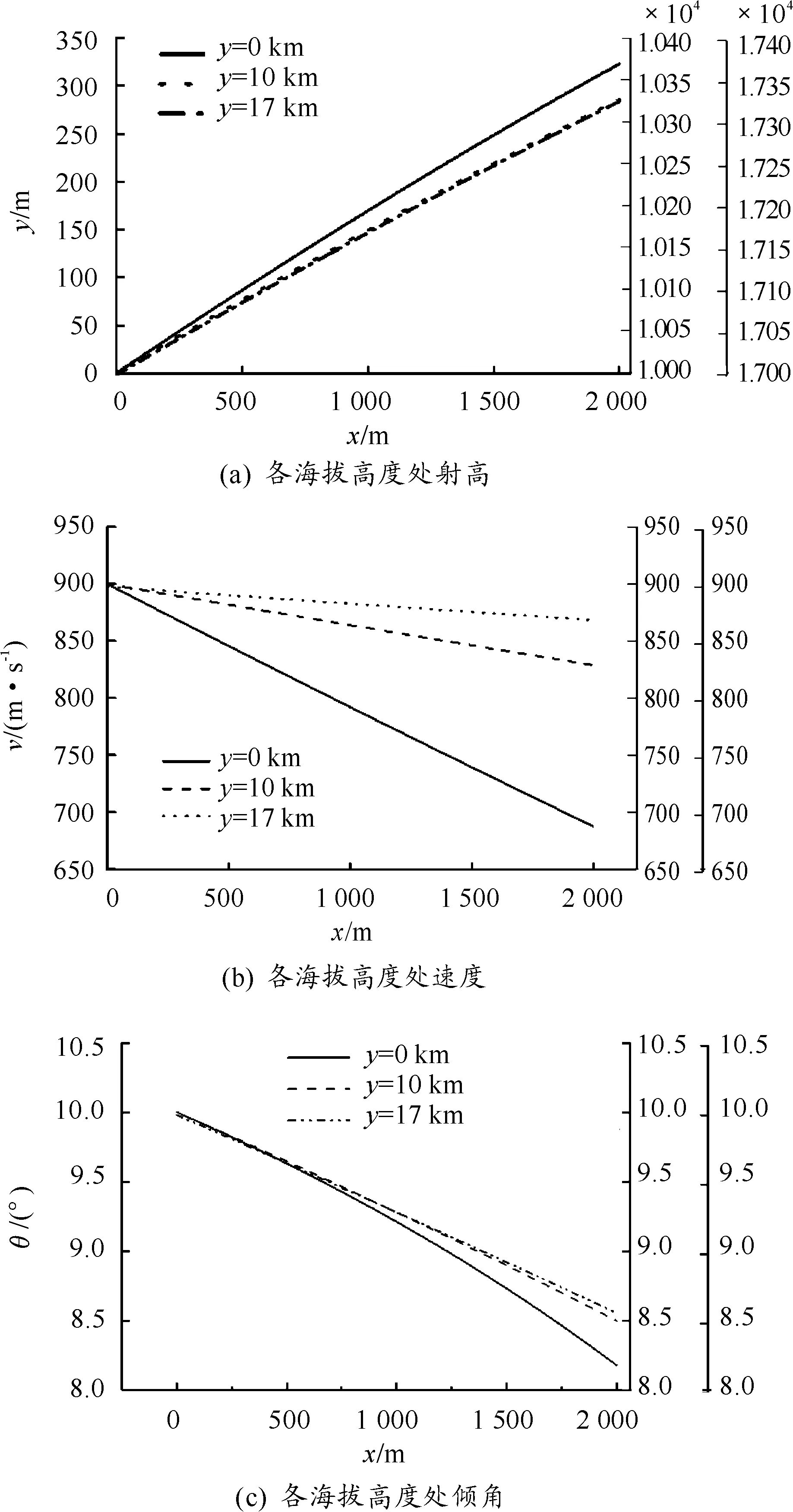
图13 不同海拔高度处弹道诸元的变化曲线

由图13可以得到：在不同海拔高度处，同一射角，初速下发射的弹丸弹道轨迹，弹丸速度，弹道倾角有较大的变化。因阻力值随着海拔高度的增加而降低，所以弹丸存速随着海拔高度的升高而增加，弹道高随着海拔高度的增加而下降，弹道倾角随海拔高度的增加而下降。

5 结论

在全声速范围内，同一马赫处，阻力系数随着海拔高度的增加而增大，且基本为线性关系；尾翼部的阻力系数随着海拔高度升高是造成整弹阻力系数升高的主要原因；在同一海拔高度处，阻力系数随着马赫数的变化规律相同。

全声速段各海拔高度处阻力系数的拟合方程具有较高的拟合精度。

在相同射角，相同初速，不同海拔处发射的尾翼弹的弹道轨迹，速度，弹道倾角不同，因其阻力值随着海拔高度的增加而降低，弹丸存速随着海拔高度的增加而增加，弹道高，弹道倾角随着海拔高度的增加而下降，需考虑海拔高度对弹道参数的影响。