尾翼倾斜角对旋转弹箭气动特性影响
2020-06-07杨文凤王学德马庚军
张 超,李 丹,田 磊,杨文凤,王学德,马庚军
(1.中国飞行试验研究院, 西安 710089; 2.南京理工大学 能源与动力工程学院, 南京 210094)
为了大幅提高不带控制系统弹箭的命中精度和稳定性,一般都采用弹箭低速旋转的方法[1],而实现弹箭旋转的方式之一是采用倾斜尾翼,但尾翼倾斜角选取得不合理,轻则导致弹箭飞行不稳定,重则导致掉弹危险。基于此背景,研究尾翼倾斜角度的大小对其气动特性影响就变得非常有意义。
DeSpirito[2]采用小扰动法对弹丸的Magnus效应进行了计算,求出Magnus力和力矩。Klatt等[3]对比风洞试验结果和采用RANS方法下的计算结果,得到了大攻角下Magnus效应的变化规律。Leroy[4]对舵身组合弹箭的气动特性计算分析表明,在大攻角下,其滚转特性和Magnus特性参数呈非线性变化趋势。Nietubicz[5]基于薄层假设的非定常Navier-Stokes方程发现边界层的非对称畸变对弹丸Magnus力的贡献最大。
2005年,高旭东等[6]比较了稳态和瞬态方法对旋转弹流场的计算结果,发现两者计算得到的动导数相差较小,但是瞬态计算时间远大于稳态时间。2011年,周德娟[7]利用旋转坐标法模拟了不同尾翼数下旋转弹的滚转特性,发现尾翼数目与滚转力矩系数呈反比关系。张超等[8]计算了不同转速下弹箭的气动特性,发现Magnus力随滚转角呈正弦变化趋势,转速与滚转力矩呈线性变化关系。石磊等[9]基于修正一方程Spalart-Allmaras湍流模型和两方程SST湍流模型计算了高速旋转的ANF(Army-Navy Finner)标模的气动力及力矩。
进入21世纪以来,各国科研工作者对旋转弹展开了系统而深入的研究,已经掌握Magnus效应、滚转特性等气动参数的变化机理,但对实现弹箭旋转的方式——尾翼倾斜角对弹箭气动参数的影响,这方面的研究文献非常少。基于此背景,本文提出基于滑移网格技术的旋转弹气动特性数值仿真方法,系统地研究尾翼倾斜角对弹箭气动特性的影响。
1 数值模拟方法
滑移网格技术具有可信度高,运行速度快等优势[9],普遍地应用在弹箭旋转的气动计算方面,图1为滑移网格区域划分示意图。
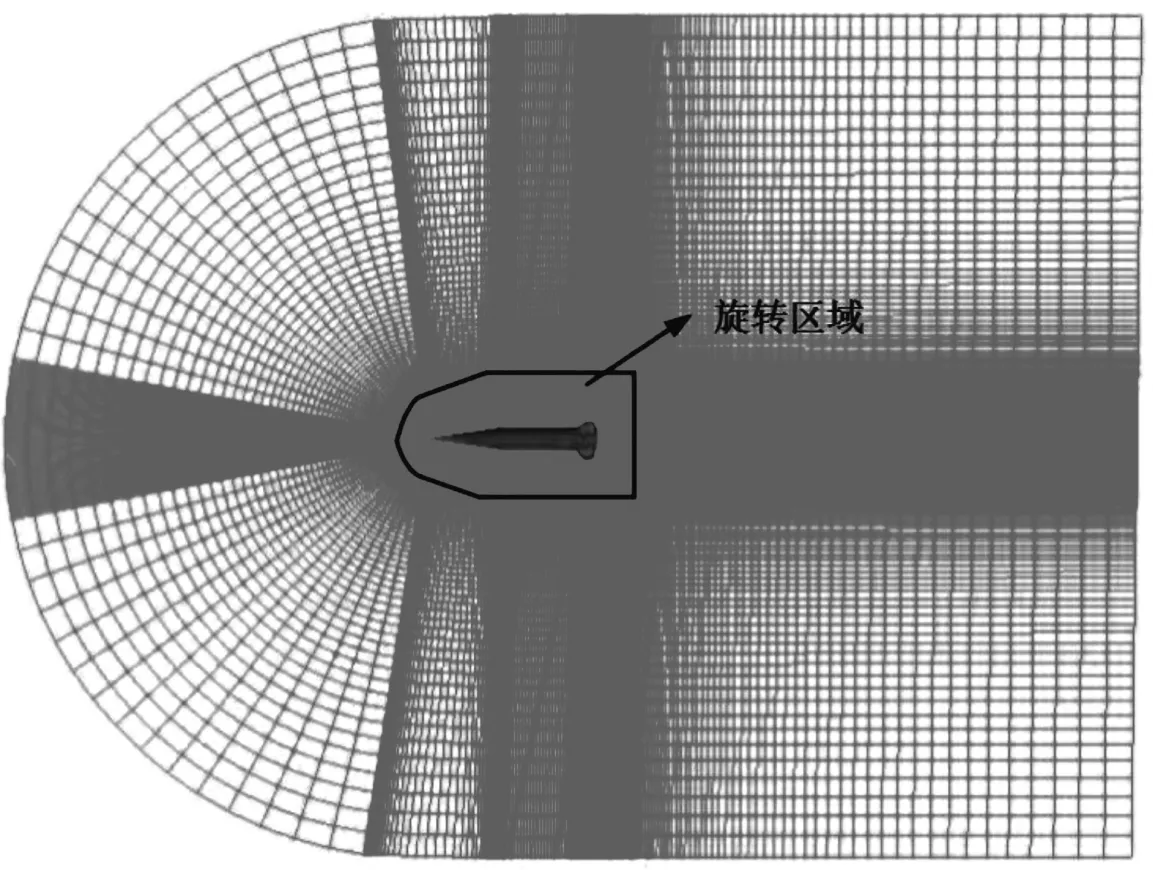
图1 滑移网格区域划分示意图
控制方程采用非定常守恒型Navier-Stokes方程组
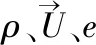
可实现k-ε湍流模型能较为准确地捕捉到旋转流动的流场细节[10-11],因此本文采用该模型进行数值仿真,空间离散采用有限体积法,对流项设置为AUSM+格式,黏性项设置为中心差分格式。
对于非定常计算结果影响较大关键参数之一是时间步长,合理的时间步长可以加速收敛所需的时间,因此本文采用双时间步长技术。
2 算法的有效性验证
2.1 验证模型
为了验证该数值仿真算法的有效性,本文选取了F4弹箭模型[7],该模型的具体尺寸如图2所示,其计算工况有关数据如表1所示,无量纲转速的计算公式为弹径(转速/声速,N为迭代次数,Δt为计算步长。

表1 计算工况
升力系数、阻力系数、绕过某一参考轴的力矩系数分别为

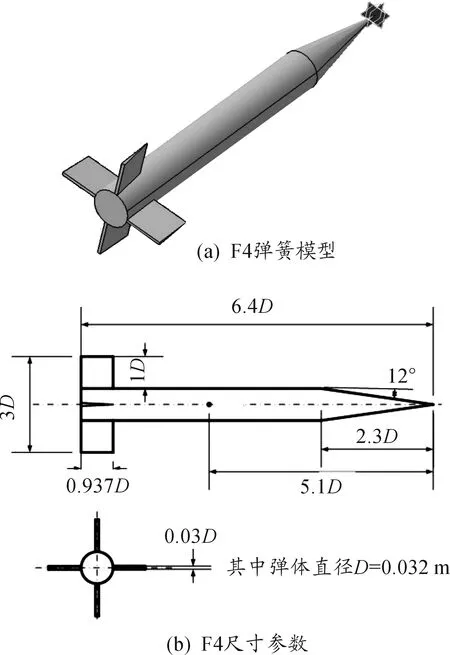
图2 F4弹箭模型
2.2 算法的有效性验证
图3给出了F4模型的气动系数随Ma值的变化曲线,并给出了相同工况下参考文献的计算结果。由图可知:文本中的计算结果与参考文献中计算值高度吻合,误差均在5%以内,因此可以说明本文选取的数值计算方法适用于全Ma数条件下,并且有较高的精度。

图3 气动系数随Ma值的变化曲线
3 弹箭Magnus效应数值计算
3.1 模型、网格和计算状态
计算模型如图4(a),其尺寸参数如图4(b)所示。弹径Dm=412 mm,重心Xmc=4.2D,弹长Dl=7.2D,翼根弦长br=1.1D,翼梢弦长bt=0.4D,网格模型如图5。选取的计算状态参数如表2所示。
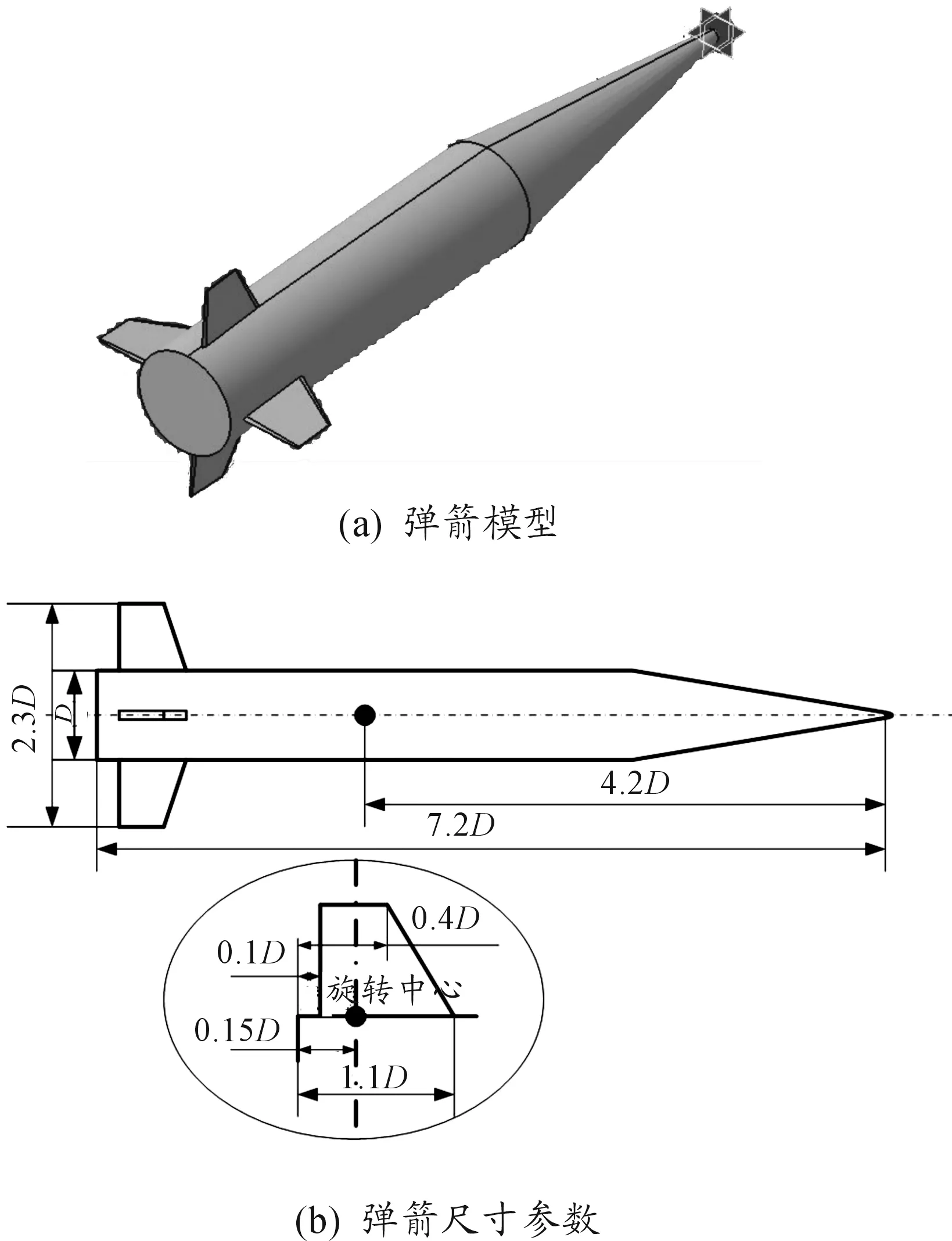
图4 模型及尺寸

图5 弹箭网格模型

表2 计算状态参数
3.2 网格和时间步长无关性验证
为了选取合适的时间步长和网格数,本文给出了Ma=1.6、α=2°、γ=1°工况下,时间步长分别为0.004、0.006、0.008以及0.01下各气动系数,如图 6所示。可见随着时间步长的不断减小,其气动特性系数趋于收敛,因此选取后续计算时间步长为0.006。

图6 不同时间步长下的气动特性系数曲线
在网格数M分别等于8×106、7×106、6×106、5×106下气动系数如表 3所示。可见随着网格数的不断增加,相邻两组网格数下的气动力或力矩的差值越来越小,表明该系数逐渐稳定。由于最后两组网格数下的计算结果差异较小(四组气动特性系数的差值分别为0.11%、0.51%、0.72%、0.76%),所以后续计算选取网格数7×106。
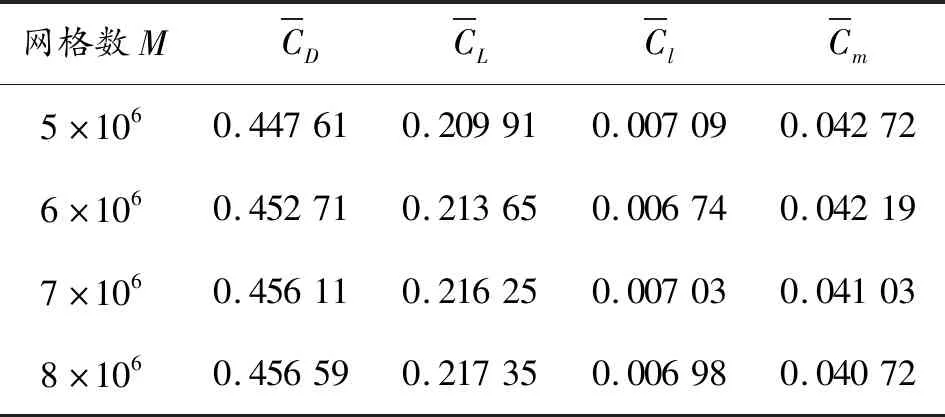
表3 网格数对气动特性系数
3.3 不同状态下的流场结构
图7给出了在Ma=2.0、α=2°时尾翼处的压力云图,其中x表示截面位置,L表示弹长,图中的1~4分别代表4片尾翼。从图 7(a)可知:弹体附近的压力较其他部分的压力高,并且呈“蝴蝶”形状分布;由于此时弹箭关于xy平面不对称,并且由于攻角产生的横流的影响,导致尾翼两侧的压力分布不对称。同时发现尾翼4两侧的压力差最大。这是由于尾翼3并未完全挡住尾翼4,尾翼4的下翼面仍然处于横流(即迎风面)中,上翼面完全处于背风区。尾翼1两侧的压力差最小,这是由于尾翼2完全遮挡了尾翼1,导致尾翼1完全处于背风区。对比图 7(a)、(b)、(c)发现:随着尾翼倾斜角的增大,尾翼1处两侧的压力差逐渐增大,这是由于随着尾翼倾斜角的增大,尾翼两侧的气流分布不均进一步加剧。
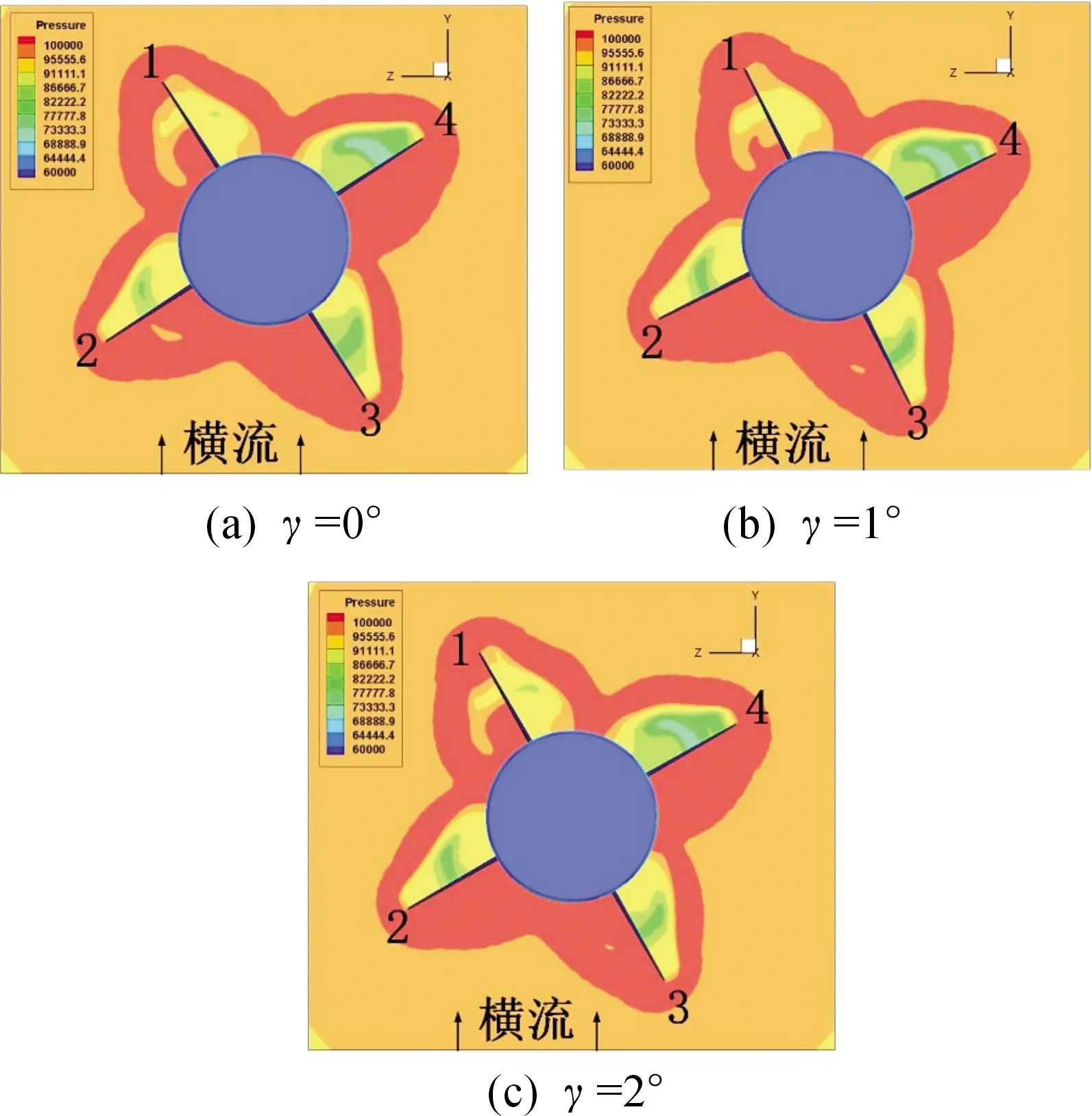
图7 不同尾翼倾斜角下尾翼处(x/L=0.95)压力云图(Ω=0.003 8)
图8给出了在Ma=2.0、α=2°时弹体不同截面的涡量强度,其中x表示截面位置,L表示弹长。同时为了更好地显示涡量强度,将涡量强度大于10万以及小于1 500的区域不予显示。由图 8(a)可知:尽管尾翼倾斜角为0,但是由于转速不为0且此时弹箭关于攻角平面不对称,因此在弹体表面以及尾翼附近产生涡流。对比图 8(a)、(b)、(c)可知:随着尾翼倾斜角的增大,气流由于混合产生的扰动加剧,从而使得涡流强度加剧。
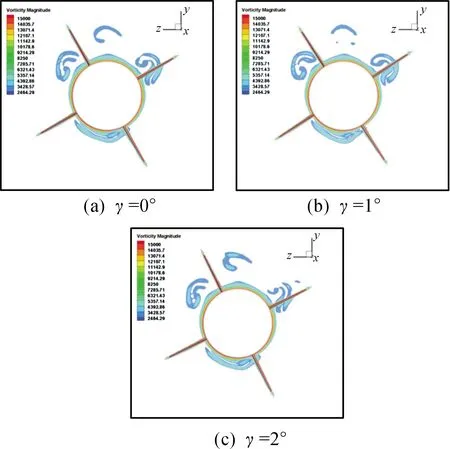
图8 不同尾翼倾斜角下尾翼处(x/L=0.95)的涡量强度图(Ω=0.003 8)
3.4 不同状态下气动特性分析
本文中弹箭模型的尾翼采用差动布置方式,即对一对尾翼而言,一片尾翼的倾斜角为+γ,则另一片尾翼的倾斜角为-γ。
从图 9可知,尾翼倾斜角从0°增加到2°的过程中,平均阻力系数处于非定比值增大趋势。这主要是因为对于一对差动布置的尾翼而言,一侧尾翼的局部附加攻角增加而另一侧尾翼的局部附加攻角减小,并且阻力系数随攻角的增大呈现非线性增加特性(近似抛物线增长规律),即由+γ引起的阻力增量远大于由-γ引起的减小量,正尾翼倾斜角引起的阻力增加量减去负尾翼倾斜角引起的阻力减小量所得的结果即为整个弹箭的阻力增加量,并且γ越大则平均阻力系数增加越明显,由表4可知,在同一Ma数下,弹体提供的阻力基本保持不变,而尾翼提供的阻力随尾翼倾斜角的增大而显著增大;表5给出了尾翼倾斜角γ引起的平均阻力系数增量。
在小攻角范围内,升力系数呈定比值(即线性变化)变化规律,因此由+γ,-γ引起的升力增大量和减小量大小相等方向相反,因此整个弹箭总升力系数随着尾翼倾斜角的变化基本保持不变。

图9 平均阻力系数和升力系数随Ma数的变化曲线
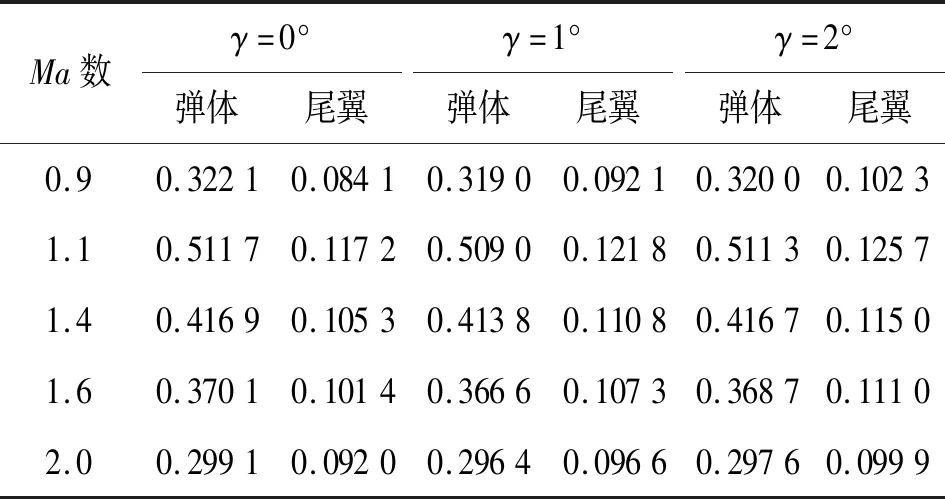
表4 4°攻角下不同部件对弹箭阻力增加量
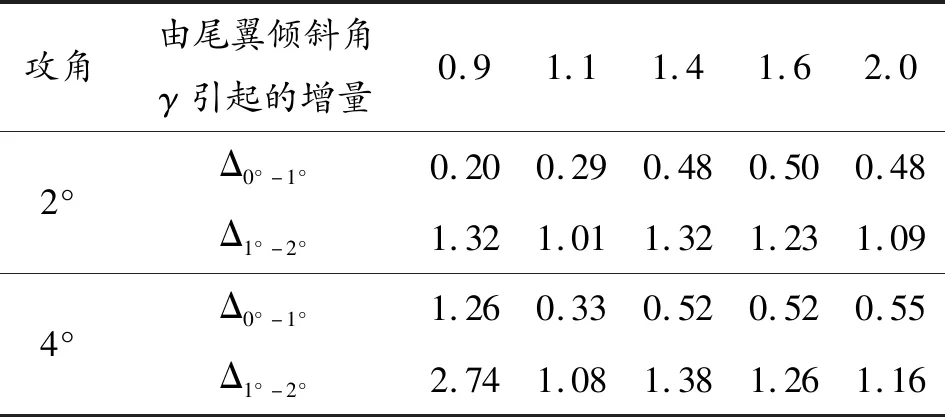
表5 尾翼倾斜角γ引起的平均阻力系数增加量 %
从图 10(a)可知,随着尾翼倾斜角从0°逐渐增大到2°,三条平均俯仰力矩系数曲线基本重合,产生该现象的原因是在小攻角情况下,升力在弹箭上的作用点不随攻角变化而变化,因此升力减小量ΔL左对质心取矩形成的俯仰力矩ΔML-左和升力增加量ΔL右对质心形成的俯仰力矩ΔML-右大小相等且方向相反,总俯仰力矩系数随着尾翼倾斜角的变化基本保持不变。
从图 10(b)可知,随着尾翼倾斜角从0°增加到2°,平均滚转力矩系数呈增大趋势,且当尾翼倾斜角为0时,该系数为负值,即为滚转阻尼力矩系数,这是由于气流黏性的存在,阻碍弹箭的旋转。当倾斜角大于0°时,该系数均为正值,这是由于空气动力引起的滚转力矩始终大于空气黏性引起的滚转阻尼力矩的缘故。由表 6可知,在同一攻角和Ma数下,随着尾翼倾斜角的增加,平均滚转力矩系数典型的定比值呈增大趋势,这是由于弹体左侧翼面产生一个向下的附加升力ΔL左而弹体右侧翼面产生一个向上的附加升力ΔL右,这两个附加升力对OX轴取矩则形成了滚转力矩,并且由于该力矩方向与参考方向相同,所以平均滚转力矩系数为正值。在小攻角时,升力随攻角呈线性变化规律,因此由附加升力产生的滚转力矩随γ的增大呈线性变化规律。

图10 平均俯仰力矩和滚转力矩系数随Ma数的变化曲线
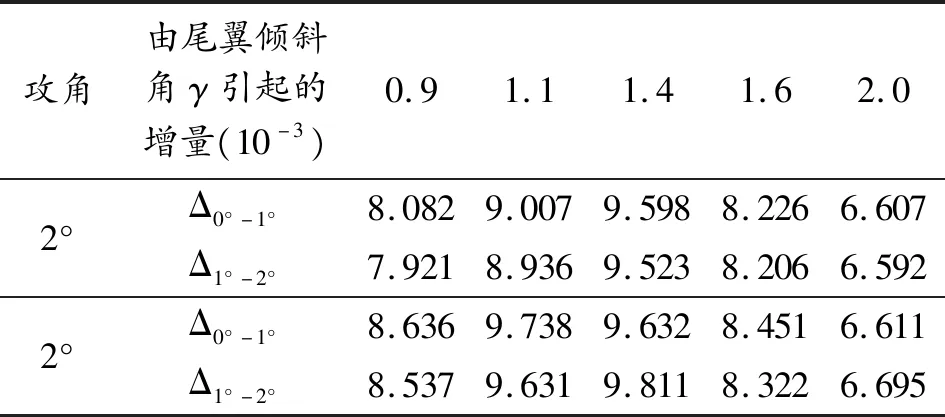
表6 尾翼倾斜角引起的滚转力矩系数增加量
由图 11可知,平均Magnus力系数随Mach数呈现先增大后下降的趋势,并且在Ma=1.1附近取得最大值;平均Magnus力系数随着尾翼倾斜角的变化呈现非定比值增大趋势;平均Magnus力矩系数的变化趋势与该系数的变化趋势一致,不再赘述。
由表7可知:对比两者所占百分比可知:全弹的Magnus力系数主要由压力分量贡献,尤其是Ma=1.1时;黏性分量对全弹的平均Magnus力系数的贡献可以忽略不计。
4 结论
1) 随着尾翼倾斜角的增加,平均阻力系数呈现非定比值增大趋势,平均滚转力矩系数呈定比值增大趋势;
2) 随着尾翼倾斜角的增加,平均升力及俯仰力矩系数不变。
3) 随着尾翼倾斜角的增大,平均Magnus力和力矩系数呈非线性增大趋势,并且相比于压差分量,黏性分量对Magnus力的贡献可忽略不计,尤其在临界Ma数附近。
