基于样本分位数原理的飞参数据异常值检测算法
2020-06-07戴邵武陈强强戴浩然
戴邵武,陈强强,2,毛 凯,戴浩然
(1.海军航空大学,山东 烟台 264000; 2.海军92728部队,上海 200040;3.空军95596部队,河南 商丘 476000)
飞行数据记录系统(Flight data recorder system,FDRS)起源于20世纪40年代,FDRS通过记录并保存飞机在飞行过程中的一些重要参数(一般称为飞参数据),实现对飞机状态的实时及事后检测[1]。飞参数据为飞机故障调查、研发设计以及训练维护提供了重要的数据来源。因此,通过对飞参数据进行准确有效的处理分析,是提高飞机可靠性的重要途径之一[2]。
在对飞参数据进行分析的过程中,受到飞行环境、仪器内部高精密、高复杂尺度的构造以及噪声干扰等多方面因素的制约,飞参数据在记录过程中会受到一定的影响[3]。通常情况下,将这些受到外界干扰而导致的飞参数据中的数据异常跳变点称为野值[4]。野值数据一般偏离记录数据的变化规律,野值的存在会给飞参数据状态估计及飞行性能分析带来较大的误差,甚至严重偏离飞机的实际飞行状态。因此在飞参数据实际使用过程中,必须对野值进行处理,从而最大限度地保证飞参数据的准确性[5]。
随着对飞参数据野值检测方面研究的不断深入,一些数学方法逐渐得到应用。其中最常用也最简单的判别准则即莱特准则[6](Letters criterion,3σ准则)。莱特准则通过对随机误差正态分布规律进行研究以进行野值剔除,但其在处理过程中假定所有观测样本均服从同一正态分布,这在一定程度上制约了适用性。文献[7-8]通过构建卡尔曼滤波器(Kalman Filter)实现对野值的识别和处理,但Kalman滤波方法需要对过程噪声及量测噪声有着明确的定义,不满足飞参数据的实际情况。文献[9]通过构建观测器/卡尔曼滤波,在无需系统噪声情况下实现了野值剔除,但该方法同样依赖于已知的系统模型。
随着对信号处理的不断深入研究,时频分析方法在野值剔除中得到了应用。文献[10]与文献[11]通过引入小波变换(Wavelet Transform,WT)对遥测、飞参数据进行分解并重构,得到了较好的野值剔除效果。文献[12]通过小波变换与Letters准则的结合,实现了对遥测数据的野值剔除与降噪。但小波分析的局限性在于小波基的选取,复杂的小波基选取对小波性能的影响至关重要,有时为了得到较好的分解结果甚至会单独构建相应的小波基,给研究过程带来了额外的计算量。文献[13]通过经验模态分解(Ensemble Empirical Mode Decomposition,EEMD)与希尔伯特变换(Hilbert Transform,HT)相结合的方法实现了飞参数据的时频分析,EEMD方法虽然在一定程度上缓解了经验模态分解(Empirical Mode Decomposition,EMD)的模态混叠问题,但其完备性不足的问题,在一定程度上造成了数据的缺失,影响了飞参数据的精度。
本文通过对样本分位数原理的分析研究,构建时间窗口对飞参数据遍历并进行样本分位数求解;通过分析样本分位数的遍历效果对飞参数据异常值进行检测。最后采用样本分位数方法对实际飞参数据进行分析,以实现对飞参数据的野值剔除。样本分位数的计算方法简单,无须进行复杂的参数及内部设置;仅对时间序列进行分析的特性使其对数据信息要求较少,是一种简单而有效的异常值检测方法。
1 飞参数据异常值检测
1.1 飞参数据异常值
根据实际情况不同,对于异常值的定义也有所不同。目前常用的定义是由Barnett与Lewis于1984年所提出的异常值定义方法:一个观测数据集中与其他数据表现不一致的一个或多个观测点所组成的子集[14]。
在飞参数据采集过程中,受到恶劣的飞行环境影响,不可避免地存在个别错误数据,异常值的存在,为后续飞参数据的处理工作带来了很大的困扰,影响着飞参数据处理的精度,甚至会带来严重偏差。这些数据值可能偏大或偏小,甚至会出现丢失情况,如图1中A、B点所示。
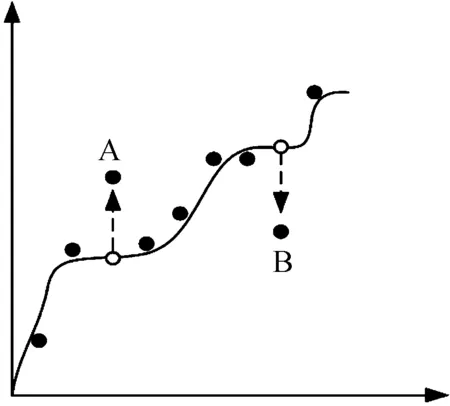
图1 数据序列的异常值示意图
通过对图1飞参数据异常值的分析可知,异常值的出现位置随机且大小未知,因此无法直接通过固定时间点或固定位置的监测实现飞参数据异常值的检测。但异常值的出现,在一定程度上对野值点附近的数值造成了影响,因此,可采用样本分位数对飞参数据序列进行分析。样本分位数是与总体分位数相对应的样本特征,反映一定比例数据集中位置的统计数据的数学特征[15]。通过对样本分位数的分析,可以统计出野值点附近的数据信息,以实现对野值点检测。
1.2 样本分位数
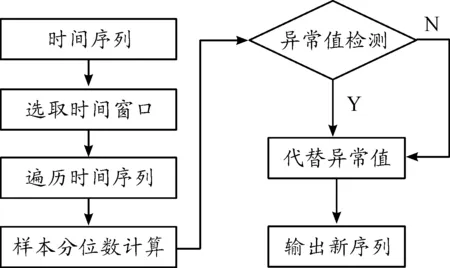
对于总体数据X及给定的a(0 图2 a分位数示意图 对于总体数据X,若X分布关于y轴对称,且存在对应的xa/2,满足P{X≥xa/2}=a,则称xa/2为X分布的双侧a分位数(双侧临界值)。如图3所示。 图3 双侧a分位数示意图 根据图2、图3中对分位数的定义,引入四分位数概念(Quantile),在统计学中,将总体数据X中所有数值从小到大排列并分成四等份,出于3个分割点位置的就是四分位数[17]。其中,第一四分位数也叫做“较小四分位数”,等于样本X中所有数值从小到大排列后的第25%的数字;第二四分位数也叫做“中位数”,等于样本X中所有数值从小到大排列后的第50%的数字;第三四分位数也叫做“较大四分位数”,等于样本X中所有数值从小到大排列后的第75%的数字。 根据定义可知,样本分位数是一个非参数统计量,能够在没有总体分布先验信息的情况下,反映出数据在选定样本X的某一时间段内的聚集程度[18]。样本分位数对于极值的影响敏感程度较弱,而且在数据预处理方面可以看出样本分位数克服了异常值点对于分析结果的影响,可有效实现奇异值点的检测[19]。 通过1.2节对于样本分位数的定义分析,结合异常值的特点,可得到基于样本分位数的飞参数据异常值检测算法,算法步骤为: 步骤1选取飞行过程中实际测量得到的某段飞参数据,共有n个数据点: X=[x1,x2,…xi,…,xn] (1) 步骤2选取时间窗口m=[xi-1,xi,xi+1],其中时间窗口m的选择结合了样本分位数的定义及数据分布的内在特性,若窗口选择过大,此时计算窗口内样本分位数时会存在对野值点的漏判;若窗口选择过小,则丧失了统计样本分位数的意义,因此选择时间窗口m=3。 步骤3根据选择的时间窗口m,对飞参数据X进行遍历,可将原飞参数据X=[x1,x2,…xi,…,xn]转换为以时间窗口m=3为固定值的多个数据序列片段X′为: X′=[(x1,x2,x3),(x2,x3,x4),… (xi-1,xi,xi+1),…,(xn-2,xn-1,xn)] (2) 步骤4对式(2)中得到的数据序列片段X′中的每个子数据序列进行样本分位数求解,得到由样本分位数组成的数据序列为: X″=[q2,…,qi,…,qn-1] (3) 步骤5由于设置的时间窗口m=3,因此公式中的数据长度为n-2。而且由于样本分位数统计的是样本之间的整体分布信息,因此可设置阈值,当X′与X″之间差值超过该阈值时,即可认为此处为异常值,并完成对整个数据序列的异常值检测。 步骤6对于检测出的异常值xi,采用一阶差分法代替该点的异常信息为: (4) 步骤7根据设置时间窗口m=3,运用样本分位数原理,即可完成对采集到的飞参数据异常值检测。基于样本分位数原理的异常值检测算法流程框图如图4。 图4 算法流程框图 以某型飞机一个飞行架次中所记录的飞参数据为例,其中,选取某个阶段的某项参数进行分析。受飞行环境的影响,飞参数据中所记录的该参数存在着噪声及异常值,所对应的飞参数据数据分布曲线如图5所示。 图5 飞参数据分布曲线 如图5所示,飞参系统记录的某型参数中的数据有N=100个采样点,并存在着异常值,这在一定程度上影响了该数据的真实有效性,根据所提出的基于样本分位数算法,设置时间窗口为m=3,则可以得到98个(N-m+1)宽度为3的由原飞参数据子数据序列组成的时间序列。对这98个时间序列进行50%样本分位数(也称为中位数)提取[20]。所得结果曲线如图6所示。 图6 基于分位数的数据提取曲线 将图6中所得的样本分位数值与原始飞参数据进行差值处理,所得样本分位数与原始飞参数据之间的误差值如图7所示。 图7 样本分位数误差值曲线 如图7所示,通过对原始飞参数据进行50%的样本分位数提取之后,野值点处的分位数波动较为明显,且误差值较大。因此,可通过样本分位数提取实现对原始飞参数据的异常值检测,并实现野值剔除。 根据公式,实现对异常值处的数据修复,经过修复后的飞参数据与原始飞参数据曲线图如图8所示。 图8 异常值检测结果曲线 如图8所示,通过设置50%的样本分位数,可实现对图5中的三处异常值点的检测,并根据异常值点修复准则,实现对检测出的三处异常值点的检测。 在50%样本分位数基础上,采用25%样本分位数与75%样本分位数对实验分析中的飞参数据进行检测,所得样本分位数与原始飞参数据之间的误差值曲线分别如图9、图10所示。 对比图9、图10与图7分析可知,25%分位数、75%分位数在三处异常值点的分位数波动较为明显,且误差值较大。证明了样本分位数原理在飞参数据异常值检测中的合理性;但相比之下,50%分位数具有更直观更明显的检测效果。总体而言,样本分位数原理仅通过对数据序列进行分析即可完成飞参数据的异常值检测,具有很好的自适应性与简洁性。 图9 25%样本分位数误差值曲线 图10 75%样本分位数误差值曲线 1) 通过设置合理的时间窗口,既保留了原始飞参数据序列的数据内部结构,又能准确提取飞参数据异常值处信息。 2) 样本分位数的选择,能够以数据的形式有效检测飞参数据的异常值,简单有效,具有实用价值。 3) 通过样本分位数方法进行异常值检测,无需获取数据的内部联系及先验信息,仅通过对数据本身进行分析即可得到准确的检测结果。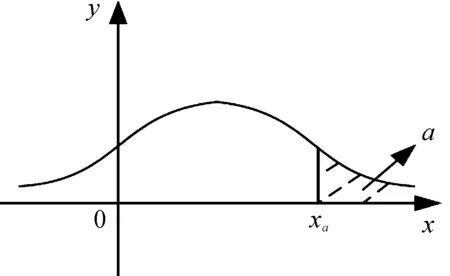

2 算法实现

3 仿真与结果分析






4 结论
