直接构造导数定义法求“不定式”极限

曾小华 蒋红珠

(1.四川师范大学数学科学学院 610068；2.广东华南师范大学数学科学学院 510631)

一、引言

我国中科院著名的李邦河院士讲：“数学根本上是玩概念的，而不是纯粹的技巧.”导数的定义在高中数学乃至是大学数学中都具有重要的作用，高中数学教学重视利用导数来研究函数的性质，如单调性、最值、极值等，但是对导数定义的教学是不够深入的，因此在高考数学中遇到求“不定式”极限时，考生往往难以解决这类问题.接下来，将对不定式极限和导数的定义相关内容作简单的介绍.

不定式极限简介若函数f和g满足：

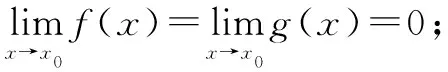
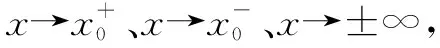
导数定义简介设函数y=f(x)在x=x0处的瞬时变化率是

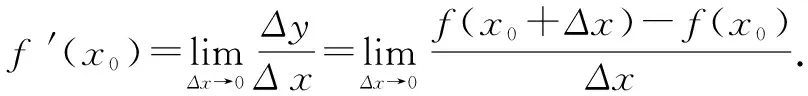
这就是函数定义在一点处的导数.

二、直接构造导数定义求解“不定式”极限

1.利用导数求不等式成立问题

例1(2017年全国高考数学文科卷Ⅱ第21题)设函数f(x)=(1-x2)ex.

(1)讨论f(x)的单调性；

(2)当x≥0时，f(x)≤ax+1，求a的取值范围.

解析问题(1)解答，略.

对于问题(2)显然可以使用分离参数法，需要进行分情况讨论.

当x=0时，显然有(1-02)e0≤a·0+1，故不等式恒成立，所以a∈R；

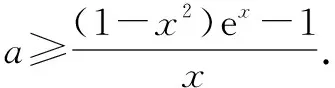
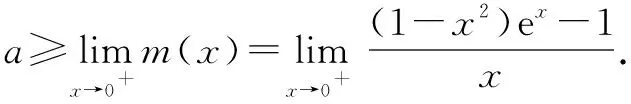
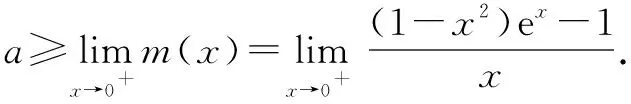
显然这是一个不定式极限，注意到分式的分母结构，考虑直接构造导数的定义.

令函数n(x)=(1-x2)ex-1，显然n(0)=0.

直接构造导数的定义，故有

该极限为函数n(x)在x=0处导数的定义，所以

所以a的取值范围为[1,+).

评注该试题为典型的求不定式极限问题，分母的结构和导数定义中的结构是完全相同的，故考虑直接构造导数的定义.巧令函数n(x)=(1-x2)ex-1，让分子的结构和分母的结构与导数定义的结构相对应起来，将不定式极限转化为求导运算.

2.利用导数定义求恒成立中参数问题

例2(2016全国高考数学文科卷Ⅱ第21题)已知函数f(x)=(x+1)lnx-a(x-1).

(1)当a=4时，求曲线y=f(x)在(1,f(1))处的切线方程；

(2)若当x∈(1,+)时，f(x)>0，求a的取值范围.

解析问题(1)解答，略.

对于问题(2)，对x∈(1,+)时，要使得f(x)>0,

即(x+1)lnx-a(x-1)>0.

由于x∈(1,+)，分离参数，可得

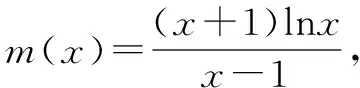
这个极限显然为不定式极限，考虑使用导数的定义.

令p(x)=(x+1)lnx，显然有p(1)=0.

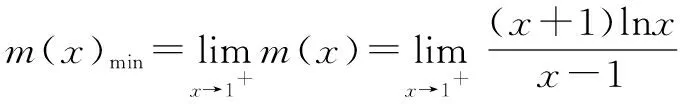
所以a的取值范围为(-∞,2).

评注该试题中巧设函数p(x)=(x+1)lnx，借助p(1)=0，将不定式极限转化为导数的定义来求解，这种以定义的方式来解决不定式极限的方法，充分体现导数定义的力量.

3.利用导数定义求参数取值范围问题

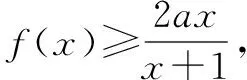
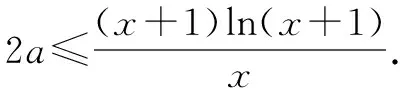
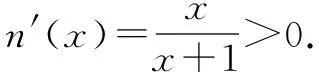
所以m(x)在区间x∈(0,+)上单调递增.

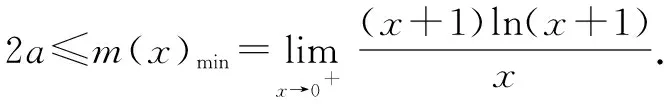
这个极限显然为不定式极限，考虑使用导数的定义.

设p(x)=(x+1)ln(x+1)，显然就有p(0)=0.

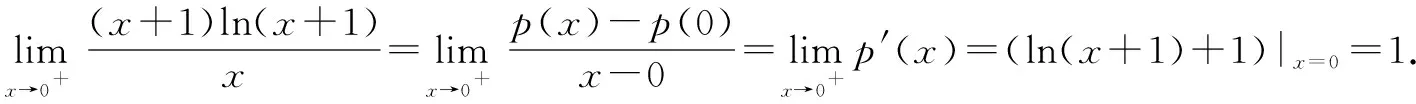
评注该试题的解决方法相对较为容易，但是其中蕴含了丰富的考点，其一是重要不等式x≥ln(x+1)；其二就是对导数定义的理解，需要理解导数所代表的几何意义和代数形式，特别是代数结构的对称性；其三是对函数的选择，需要充分地考虑分母的结构形式，需要将选择的函数与分母对应起来，这需要考生具有敏锐的洞察力.

4.利用导数定义求最值问题

(1)求证f(x)≤0；

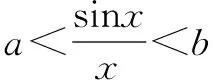
解析问题(1)解答，略.

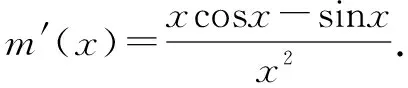
由问题(1)可得，函数f(x)=xcosx-sinx≤0.

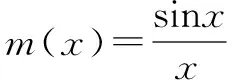
现在需要求a的最大值与b的最小值.

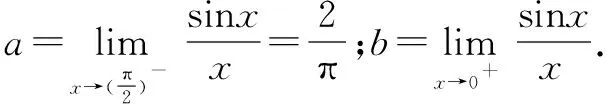
显然갨为一个不定式极限，故考虑构造导数的定义.令n(x)=sinx，显然有n(0)=sin0=0.

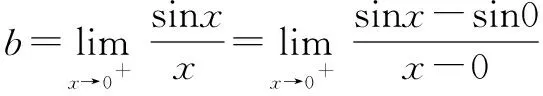
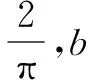
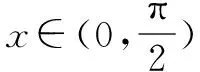
通过对上述不定式极限试题的分析和解答，可见当所求的极限为不定式极限且分母为一次单项式或者是一次二项式的时候，可以将求不定式的极限值问题转化为导数的定义来求解.在求解这类型的不定式极限值时，需要注意导数定义的结构和构造的函数结构是否相匹配，只有当分子与分母的结构相匹配时才能使用导数的定义.含有不定式极限问题的试题，多具有高等数学的知识背景，可以通过高等数学中的“洛必达法则”解决，解决方法较为简单，但在高中数学教学和解题中不建议使用，不然容易让学生产生惰性思维，不利于学生数学思维的培养，有兴趣的可以参看高等数学中求不定式极限的常用策略.