2019年浙江高考第22题(Ⅱ)的三种解法

钟建新

(浙江省春晖中学 312300)

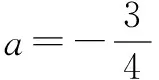
注：e=2.71828…为自然对数的底数.

解法1(1)略.

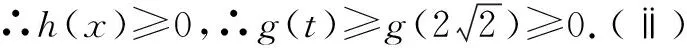
解法2(1)略；

解法3(1)略.

感悟解法1与解法2利用了导数来研究函数的单调性、极值与最值，而解法3则巧妙地利用了不等式：lnx≤x-1,x>0解题，过程显得更为简洁完美，思维要求更为高级.为使解题朝着简单、容易的方向转化，以上三种解法都用到了换元的方法.

解题其实也是一个发现过程，在解完题后再来反思一下，看看有没有别的解法，长期如此，我们的发现能力、创新能力就能得到极大的增强.通过解题研究和归纳总结，我们能够形成数学意识，提高解题水平，陌生奇妙的技能技巧就会成为我们熟练掌握的通性通法，数学素养的提升就会水到渠成.