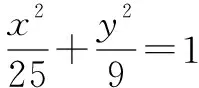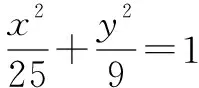巧用定义突破难题二例

李昌成

(新疆乌鲁木齐市第八中学 830002)

众所周知，解析几何是利用解析式来研究几何对象之间的关系和性质的一门几何学分支，亦叫做坐标几何.简言之，解析几何用代数来研究的几何.既然是几何，那么它就有图形特征.因此，除了计算以外，利用圆锥曲线的定义，借助几何性质解题，也是我们必须高度重视的.

一、直接应用定义解题

数学中的定义是对一个概念的内涵和外延的确切而简要的说明.因此，定义具有性质定理的功能.当知道圆锥曲线的类型时，我们可以应用定义(式)解题.

例1 (2012年全国高考Ⅱ卷理科第20题) 设抛物线C:x2=2py(p>0)的焦点为F，准线为l，A∈C，已知以F为圆心，FA为半径的⊙F交l于B,D两点.

(2)若A,B,F三点在同一直线m上，直线n与m平行，且n与C只有一个公共点，求坐标原点到m,n距离的比值.

分析本题中圆心和抛物线的焦点重合，因此一些线段具有双重身份，恰当利用定义可以建立一些关键等式，挖掘出一些表象上的未知量，突破难点.

(1)解由对称性知：△BFD是等腰直角三角形且斜边BD的高为h=p①，

众所周知，日语在大量汲取外来词汇的基础上形成了自身独特的语言系统。明治维新以前，以汉字词为主的外来词汇大量进入日本，成为了日语的重要组成部分。明治维新以后，日本开始全面接触西方诸国的新思维与新理念，承载着各种新概念与新事物的新词也被大量引入日本，以音译词为特点的该类词汇成为了近代以后日语的另一重要组成部分。

(2)解法1因为A,B,F三点在同一直线m上，所以AB为⊙F的直径，∠ADB=90°.

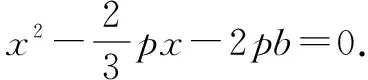
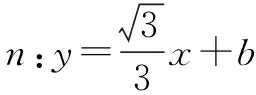
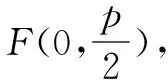
评注本题在解答过程中反复运用了圆的定义，抛物线的定义，突出了定义的性质定理的功能，巧妙地将二者有机结合在一起，得到了文中①②③④处的方程或值.这是本题的重要突破口，若仅仅依靠运算，解答将陷入困境，无法推进.

二、构造定义形式解题

定义具有判定定理的功能.因此，我们可以构造圆锥曲线的定义式，判断其类型，在构造中赋予代数式几何意义，实现等价转化的目的.

例2 已知点A，B关于坐标原点O对称，|AB|=4，⊙M过点A，B，且与直线x+2=0相切．

(1)若A在直线x+y=0上，求⊙M的半径；

(2)是否存在定点P，使得当A运动时，|MA|-|MP|为定值？并说明理由．

分析若动点M的轨迹是双曲线或抛物线，由双曲线和抛物线的定义知，|MA|-|MP|可能是定值.若动点M的轨迹是双曲线，则A,P应该是定点(焦点)，这不可能，那么动点M的轨迹因该是抛物线，我们可将问题向抛物线转化.

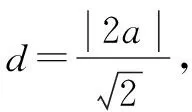
由①②联立解得R=2，或R=4.

(2)因为线段AB为⊙M的一条弦，

所以圆心M在线段AB的中垂线上，设点M的坐标为(x,y)，则|OM|2+|OA|2=|MA|2，又因为⊙M与x+2=0相切，所以|MA|=|x+2|，所以x2+y2+4=|x+2|2，整理得y2=4x.

所以圆心M的轨迹是以F(1,0)为焦点，x=-1为准线的抛物线，结合抛物线的定义，|MA|-|MP|=|x+2|-|MP|=|x+1|-|MP|+1=|MF|-|MP|+1(ⅱ).

所以当点P与点F重合，|MA|-|MP|为定值1，即P的坐标为(1,0)，所以存在定点P(1,0)使得当A运动时，|MA|-|MP|为定值．

评注本题考查了圆和抛物线的定义以及直线与圆的关系，又考查了待定系数法和曲线轨迹方程的求法，属于难题．(ⅰ)处起到了消元的作用；(ⅱ)处通过构造，赋予目标式几何意义，正是建立在定义基础之上，问题才得以突破，纯计算会导致一筹莫展.没有经过训练，学生难以实现此转化.

三、解法提炼

定义是数学中最原始的概念，简单而朴素，因此很容易被学生遗忘.殊不知，有时它却是解题最有力的工具.运用圆锥曲线的定义解题，通过数形结合，不仅能抓住问题的本质，而且能够避开繁杂的运算，使问题巧妙得解.要想做到熟练运用定义解题需要注意以下事项：

1.全面准确地掌握定义，包括从文字语言、图形语言、符号语言的角度，这样才能把握住运用的时机.

2.定义具有双重功能，既能作为判定定理，又可以作为性质定理，我们要二者兼顾，融会贯通.

3.高度重视定义之间的区别与联系，防止张冠李戴，弄巧成拙.

4.注意多个定义联合应用，同一个量的多重身份往往把问题变得扑朔迷离.

5.培养返璞归真的意识，在日常学习中多多留意，关键的时候定义方可派上用场.

四、牛刀小试