例析二体问题的折合质量解法
2020-06-06谢汝成
谢汝成
(吉林省辽源市第五中学 136200)
孤立的二体系统问题在高考试题和自主招生试题中比较常见,在解决该类问题时,通过引入折合质量的概念,可将复杂的二体问题变为单体问题.本文利用三道题目的分析求解,凸显出该种方法在解决此类问题的巧妙之处.
一、折合质量推导
如图1所示,宇宙中两颗相距较近的天体均为“双星”,它们以二者连线上的某一点为圆心做匀速圆周运动,而不至因为万有引力的作用而吸引到一起.设两者的质量分别为m1和m2,两者相距L.
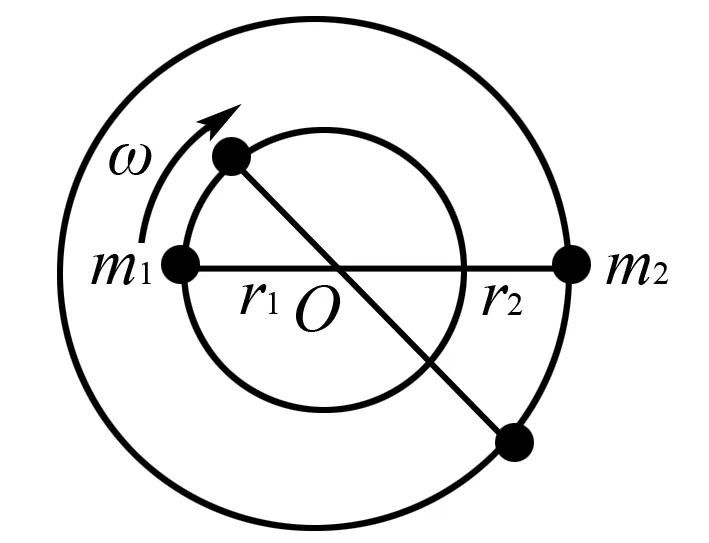
图1
双星m1和m2
ω1=ω2=ω
①
②
r1+r2=L
③
分析m1的匀速圆周运动
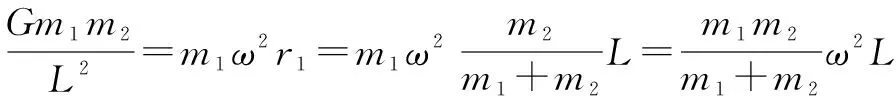
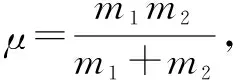
二、应用
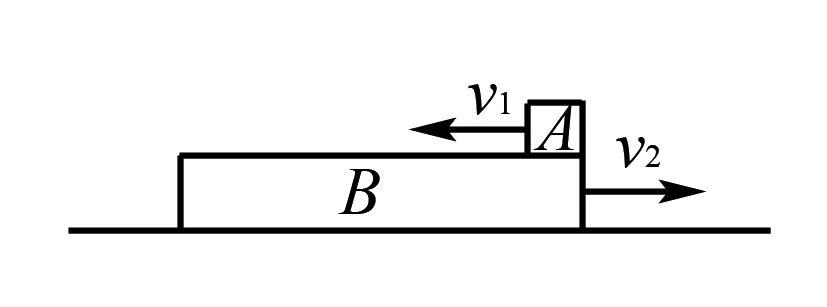
图2
例1如图2所示,一质量为mB长方形木板B放在光滑的水平地面上,在其右端放一质量为mA的小木块A,现以地面为参照系,给A和B以方向相反的初速度V1和V2,使A开始向左运动,B开始向右运动,但最后A刚好没有滑离B板.若已知A、B之间的动摩擦因数为μ.求满足条件的木板至少为多长?
解析以B为参考系,则滑块A的折合质量为
①
A相对B的初速度VAB=V1+V2,当A相对B静止时在B上相对滑动位移最大.
②
注:本题的常规解法为相对运动或等效完全非弹性碰撞模型,但计算过程较上面的解法略复杂.
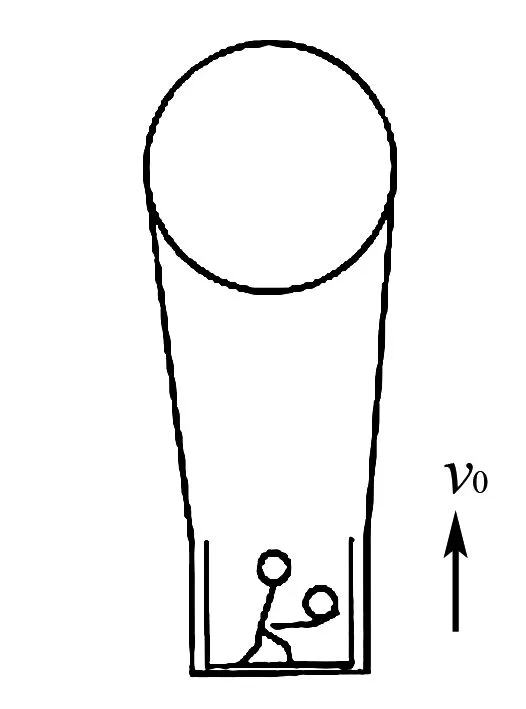
图3
例2如图3所示,一人手持质量为m的小球,乘坐在热气球下的吊篮里,气球、吊篮和人的总质量为M,气球以速度v0匀速上升,经过时间t0后接到小球.若人手在抛接小球时相对吊篮的位置不变,求抛球过程中人做的功.
解析以M为参考系

①
m相对M以速度v′竖直上抛
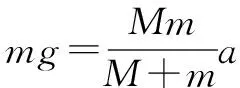
③
④
以地面为参考系,设抛出重物后M的速度变为v2,m对地的抛出速度为(v′+v0)
浮力和重力平衡,系统动量守恒:
m(v′+v0)+Mv2=(M+m)v0
人做的功等于系统动能增量:

例3 (2015中科大自主招生)两个带点小球所带电量相等,符号相反.质量分别为m和2m,初始时刻,它们间距离为d,小球2m静止.小球m沿着与两者连线垂直的方向以速度v运动.随后,它们多次处于相距3d的位置上,求小球所带的电荷量.
知识准备:
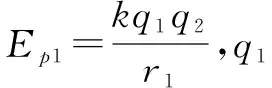
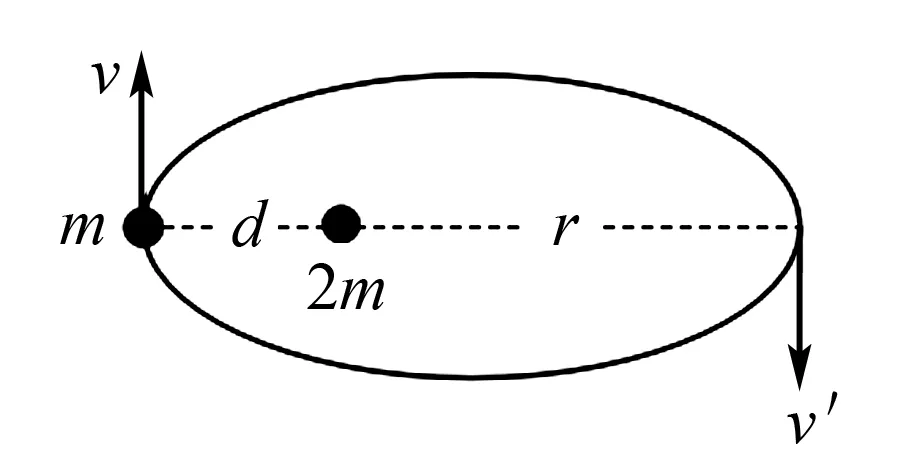
解析(1)以2m为参考系,m绕2m转动,轨迹为椭圆,2m处于椭圆的焦点.m的初始位置距离2m最近为d,距2m最远点r满足:
r≥3d
①
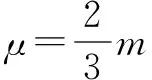
②
设m运动到椭圆轨道最远点的速度为v′
由角动量守恒有:mvd=mv′r
③
对椭圆长轴两端点列能量守恒:
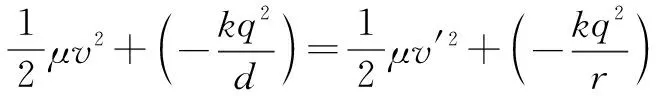
④
(2)两球多次处于相距3d,故m不能到达无穷远.
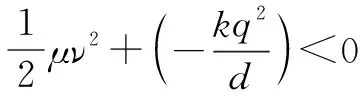
⑤
折合质量的引入,为两体碰撞、类碰撞,双星系统,特殊简谐运动等问题的分析求解提供了一个明显便捷的计算方法,适用范围广,但在应用的过程中应重点关注的是:折合质量的概念仅适用于孤立的两体系统,即不受外力的系统.若系统受外力,本解法将不再使用.
