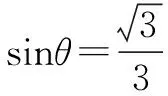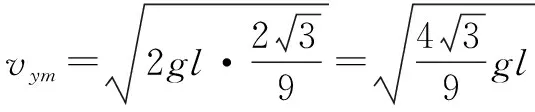竖直面内变速圆周运动中极值问题的解法

袁 茵

(安徽省砀山中学 235300)

题1 如图1所示，一个质量为M的人站在称盘上，人拉着一根长L的轻绳的一端，绳的另一端拴着一个质量为m的铅球，若让铅球在竖直平面内做圆周运动，当运动到最高点A受到绳子的拉力恰好为mg，铅球可看做质点.问：铅球在运动过程中，运动到何处，称盘上的读数最小值为多少？

解析设铅球运动到A点时速度为vA，运动到P点时(如图2所示)称盘上读数最小，值为N，其中OP与竖直方向夹角为θ，P点速度设为vP，轻绳对铅球的拉力为T，在A点，有：

铅球从A点运动到P，有动能定理得：

在P点，在法向上，由牛顿第二定律，得

称盘上读数N=Mg-Tcosθ.

可得N=Mg-4mgcosθ+3mgcos2θ，

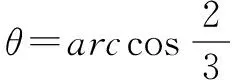
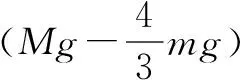
在本例题中，秤盘上的读数最小不是小球运动到最高点的时候，有的同学凭着以往解题的经验，不假思索，就当成小球运动到最高点的时候去解题，很容易出现错误.

题2 如图3所示，在质量为M的飞轮上固定着一个质量为m的重物，重物到转轴的距离为r,重物随电动机一起转动，为使电动机不从地面跳起，则电动机的飞轮角速度不超过多少？若以上述角速度匀速转动，电动机对地面最大压力是多少？

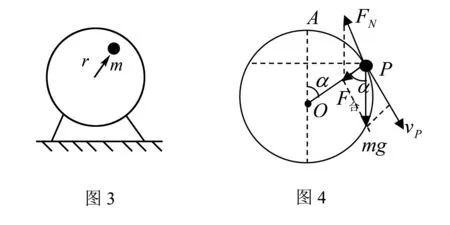
解析如图4所示，当重物运动到P处电动机对地面的压力最小，OP与竖直方向的夹角为α.由于重物随电动机做匀速圆周运动，

有F合=Fn=mω2r，

则电动机对地面的压力为

N=Mg+mg-mω2rcosα.

由上式可知，当α=0时，即重物到达最高点时，电动机对地面的压力最小，电动机不从地面跳起的临界条件为：N=0.

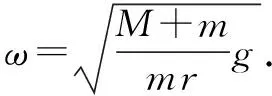
同理可得，当α=π时，即重物运动到最低点时，电动机对地面的压力最大，最大值为Nmax=2(M+m)g.

在本题中，与题1不同，电动机匀速转动，重物的速率不变，所以经过推导重物运动到最高点时电动机对地面的压力最小.

题3如图5所示，在倾角α=30°的、质量为M的斜面上，有一根长为L=0.8m的细绳，一端固定在O点，另一端系一质量为m=0.2kg的小球，小球沿斜面做圆周运动，在A点绳中的拉力为1N.那么小球运动到哪里，斜面对地面的压力最小？压力是多大？

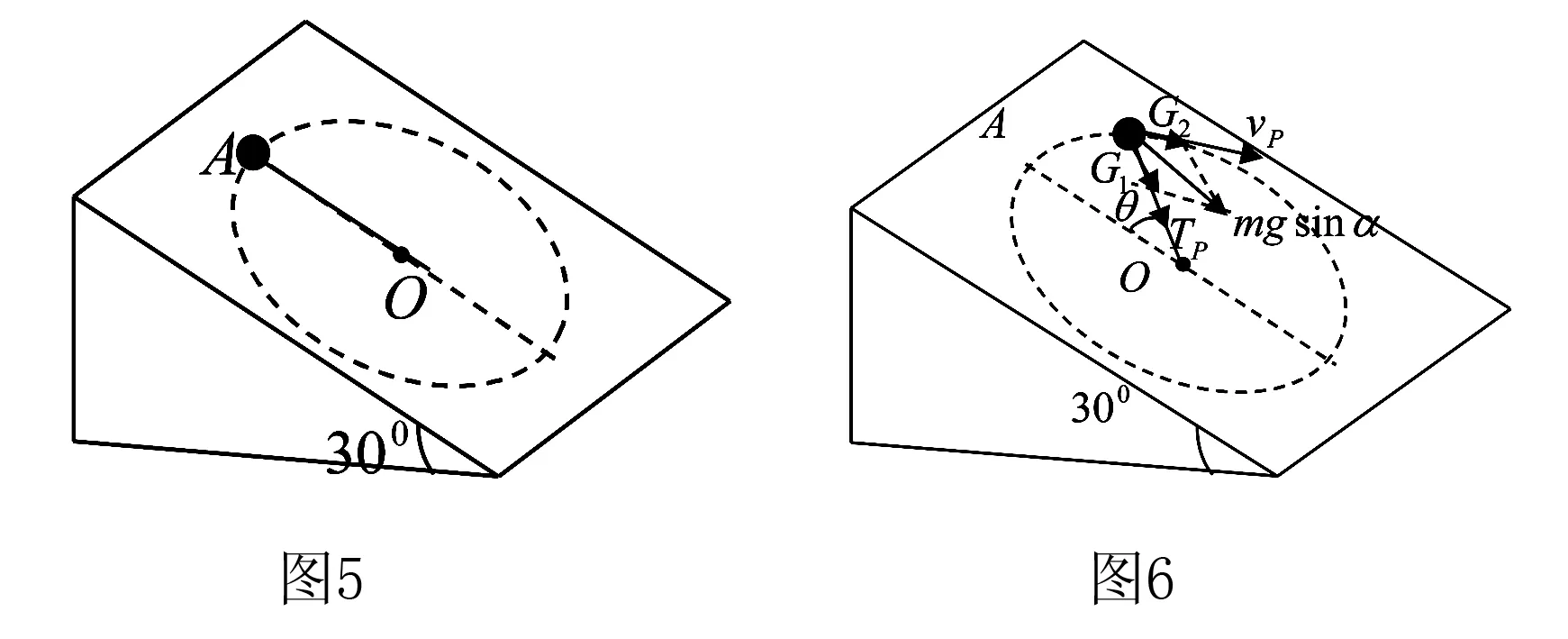
解析如图6所示，设小球在A点速度为vA，绳中拉力为TA，沿绳有

当小球运动至P点时，斜面对桌面压力最小，此时

绳与AB的夹角为θ，速度为vP，绳中拉力为TP,沿绳有

从A点运动到P点，有动能定理有

斜面对地面的压力

本题虽不是竖直平面内的情形，但是属于类竖直平面内变速圆周运动，分析方法相同，只不过把竖直平面内竖直向下的重力mg等效成了mgsinα，采用类比的方法使得问题简化.

题4如图7所示，细线的上端固定，下端系一小球，细线长为l，将小球与细线拉至同一水平位置后从静止开始释放，求小球的细线运动到与水平方向成多大角度时，小球获得最大的竖直分速度(用反三角函数表示，重力加速度为g)

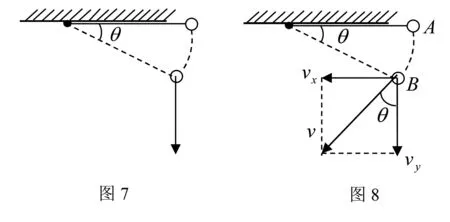
解析设小球质量为m，当细线运动到与水平方向夹角为θ时，小球获得的速度为v，竖直方向的分速度为vy，如图8所示：由动能定理，小球从A运动到B，有

又vy=vcosθ，

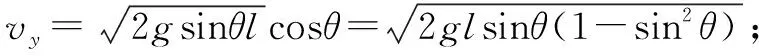
下面考虑函数f(θ)=sinθ(1-sin2θ)，令sinθ=t,t∈[0,1],

则y=t(1-t2)=t-t3，