化归思想在高中数学解题中的应用研究

王宏利

(福建省光泽第一中学 354100)

高中数学试题类型复杂多变，运用直接转化法、换元法、数形结合法、构造法等进行化归，可降低数学试题难度，大大提高解题正确率，因此，授课中应注重这些化归方法及其应用讲解，提高学生化归思想应用意识，使其掌握这一解答数学问题的重要技巧.

一、直接转化法的应用

直接转化法是一种将数学问题转化为基本公式、基本定理顺利求解数学问题的方法.为使学生能够熟练应用这一化归方法，一方面，授课中为学生深入讲解基本公式，基本定理，使其既要牢固记忆，又要清楚其来源，积累丰富的基础知识.另一方面，结合具体题目，讲解直接转化法的应用，使学生体会应用过程，掌握应用技巧.

二、换元法的应用

换元法指通过引入新的变量将分式化为整式、将高次化为低次，简化解题过程的一种方法.换元法在方程、不等式、函数等试题中应用广泛.为使学生掌握该化归方法，一方面，讲解换元常用方法，包括均值换元、三角换元、局部换元等，细致剖析各种换元形式以及应注意的问题.另一方面，优选经典题目，为学生讲解换元法的应用，掌握换元技巧，提高解题正确率.

例2已知x、y∈R，满足x2+2xy+4y2=6，则z=x2+4y2的取值范围为：____.

该题目题干较为简单，但如不会进行化归很难解答.认真观察题干特点，可采用三角换元法进行解答.

三、数形结合法的应用

数形结合法是通过建立“形”与“数”之间的相互联系，进行巧妙转化，解答数学问题的一种回归方法.数形结合法可简化解题步骤，提高解题效率.为使学生灵活应用该种方法，一方面，讲解“形”与“数”转化的实现途径.如“形”向“数”转化可采用向量法、构建坐标系等方法.“数”向“形”的转化则主要根据经验利用函数以及平面、立体几何知识绘制对应图形.另一方面，围绕具体例题，讲解数形结合法在解题中的应用，使学生体会数形结合法解题的简便之处，认真学习与应用数形结合法解题.

图1

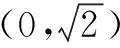
四、构造法的应用

构造法指结合已学知识以及经验，构造一个合适的数学模型，将问题变为易于解决的问题.构造法对学生的综合能力要求较高，为使其灵活应用，教学中，一方面，注重讲解常用构造法，包括构造一次函数、二次函数、构造向量等，加深学生对构造法的理解，掌握构造法精髓.另一方面，结合具体习题，鼓励学生采用构造法求解，并给予学生相关指导，树立应用构造法解题的自信，提高学生构造法应用技巧及应用能力.

例4已知等比数列{an}中a1=2，a8=4，函数f(x)=x(x-a1)(x-a2)…(x-a8)，f′(0)=( ).

A.26B.29C.212D.215

该题目技巧性较强，很多学生感觉无从下手，因此，授课中引导学生认真观察已知条件，提示其使用构造法进行求解.事实上，通过构造函数f(x)=xg(x)而后运用整体代换与数列性质不难求解.

令g(x)=(x-a1)(x-a2)…(x-a8)，则f(x)=xg(x)，两边求导得到：f′(x)=g(x)+xg′(x)，∴f′(0)=g(0)=a1·a2·…·a8.

又∵{an}为等比数列，a1=2，a8=4，∴由等比数列性质可得，f′(0)=g(0)=a1·a2·…·a8=(2×4)4=212.正确选项为C.

化归思想是解答高中数学试题的重要思想，涉及的化归方法较多，其中直接转化法、换元法、数形结合法、构造法较为常用.授课中既要注重化归思想以及常用方法的讲解，使学生储备丰富的理论知识，又要结合具体例题，讲解化归方法的应用，使其掌握化归方法应用技巧，提高高中数学解题能力，为数学成绩的提高奠定坚实基础.