一个函数不等式恒成立问题的两种解法
2020-06-06曹彬
曹 彬
(贵州省黔西第一中学 551500)
函数作为高中数学知识体系的核心,是历年高考的热点,函数题常常作为高考压轴题出现.以研究函数性质为主要解题手段的不等式称为函数不等式,函数不等式恒成立问题是高考函数题中的重点,在高考试卷上较为常见.通常以一次函数、二次函数、三角函数、指数与对数函数为载体,考察函数的图象与性质,渗透换元、转化与化归、数形结合、函数与方程等思想方法,考查学生的综合解题能力,在培养思维的灵活性、创新性,发展学生数学核心素养起到积极的作用.
函数不等式恒成立问题都要转化为函数最值问题,但对于解析式较复杂的函数,学生普遍感到难以找到解决问题的切入点和突破口.本文旨在介绍洛必达法则应用的同时,多种解法求一类特殊函数不等式恒成立问题中参数取值范围.
一、问题的提出
已知函数f(x)=(x+1)lnx-a(x-1),若对任意x∈(1,+∞),都有f(x)>0恒成立,求常数a的取值范围.
这种问题通常转化成讨论f(x)在(1,+∞)上的最小值,而且常常用参变分离方法.如果仔细观察,会发现f(1)=0,这种问题的解法就有数形结合法、参变分离法,下面分别介绍这两种解法.
二、问题的解答
1.解法一(数形结合法)
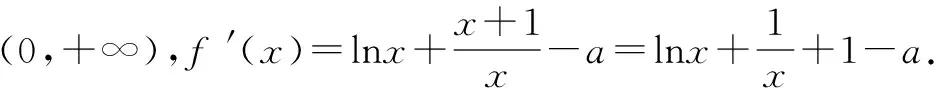
因为x>1,所以g′(x)>0恒成立,所以g(x)在(1,+∞)上为单调增函数,且g(1)=f′(1)=2-a.
当2-a≥0,即a≤2时,f′(x)>0在(1,+∞)上恒成立,所以f(x)在(1,+∞)上为单调增函数.由于f(1)=0,故满足f(x)>0在(1,+∞)上恒成立.
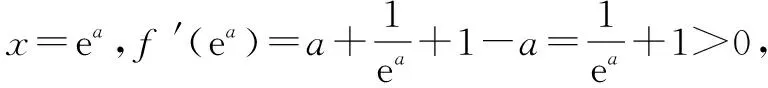
综上,a≤2.
评析这种解法就是参考答案给出的常规解法,根据函数的性质确定函数的图象,通过讨论函数在指定范围内是否有零点,逐步缩小参数的范围并最终确定,但是找区间的端点是难点.
2.解法二(参变分离法)
洛必达法则 设函数f(x)和g(x)满足:
(2)函数f(x),g(x)在x0的某个去心邻域内可导,且g′(x)≠0;
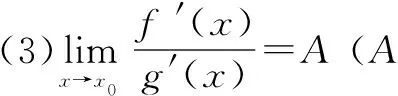


评析这是最容易找到入手点的解法,但在最后阶段却出现疑惑,因为在x=1处的函数值不能直接解出,所以要用洛必达法则求极限值.
运用上述两种解法,可解决如下同类型题:已知函数f(x)=(1-x2)ex,当x≥0时,都有f(x)≤ax+1恒成立,求a的取值范围.
函数题的得分率历来不高,学生普遍感到困难,分析有如下原因:需要对证明的等式或者不等式进行变形,此过程需要技巧,经验性很高,学生一般很难掌握;含有参数的问题需要分类讨论,讨论的类别较多,运算量大还容易遗漏;对研究的函数不能画出图象,难以构造出直观模型辅助思考;很多函数题需要多次求导.
所以,如果用高中知识解答高考函数题,对学生的思考灵活性、思维严密性、表达逻辑性等方面的要求较高,难度较大.
