直线与圆的位置关系中的二变元问题的最大值问题探析

庄 顺

(福建省厦门第六中学 361000)

在近年的高考题、自主招生题、竞赛题或模拟题中，经常会有求解涉及双变元或多变元问题中的最值或取值范围问题．此类问题由于变元较多，切入点没有太大规律，往往导致难度较大，且比较难加以突破．也正是由于变元较多，此类问题破解的思维方式多变，切入点众多，方法有时也多样．

【高考真题】(2018·北京理·7)在平面直角坐标系中，记d为点P(cosθ，sinθ)到直线x-my-2=0的距离．当θ，m变化时，d的最大值为( ).

A．1 B．2 C．3 D．4

思维角度1：三角函数法

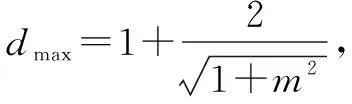
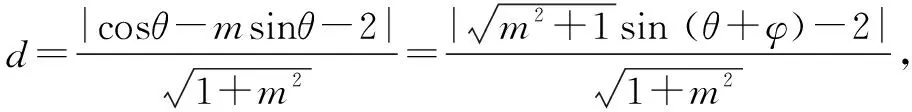
点评把点到直线的距离问题转化为含有二元函数θ、m的最值问题，分别结合三角函数、二次函数的性质，依次来转化，进而得以确定相应的最值问题．在这里的解决关键是对二元函数θ、m没有直接关系的条件下，分别有针对性地处理，从而得以转化与应用．

思维角度2：数形结合法

分析根据题条件确定点P的轨迹与直线恒过定点A(2，0)的性质，先让直线x-my-2=0保持“静止”时确定点P到直线的距离的最大值问题，再进一步让直线x-my-2=0进行“转动”，通过数形结合来确定最值即可．

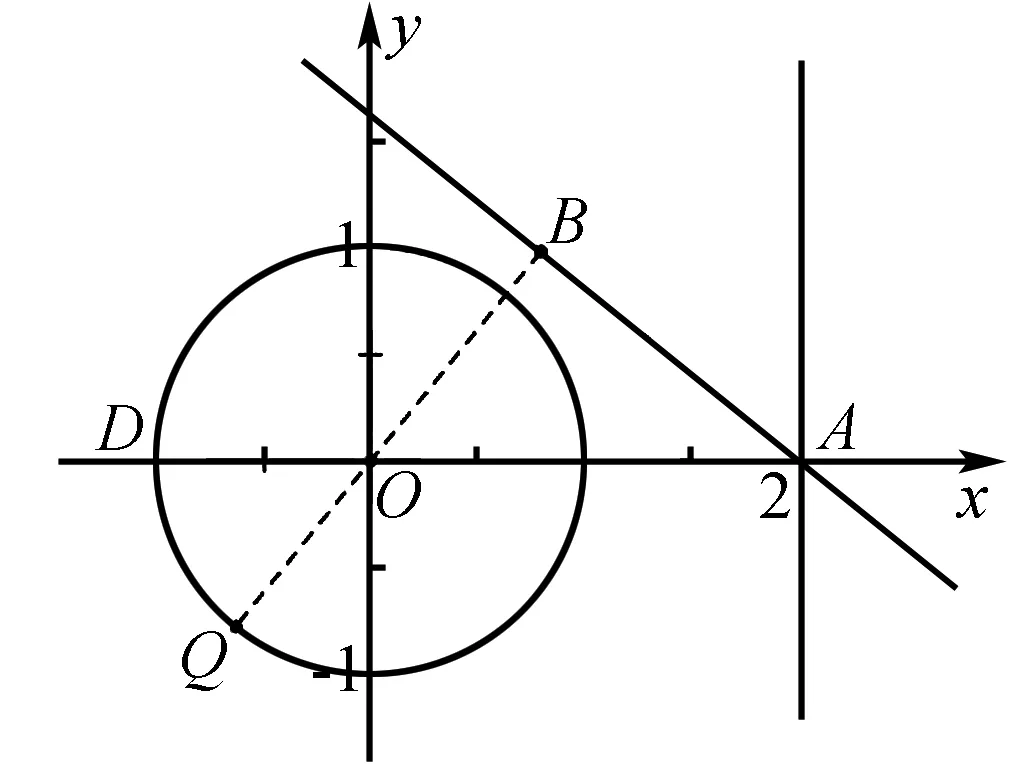
解法2 由于点P(cosθ，sinθ)，则知点P的轨迹是单位圆O：x2+y2=1，而直线x-my-2=0恒过定点A(2，0)的动直线，如图所示.先让直线x-my-2=0保持“静止”，过O垂直于直线x-my-2=0的直线交单位圆O：x2+y2=1于点Q，交直线x-my-2=0于点B，而单位圆O：x2+y2=1与x轴的负半轴交于点D.根据平面几何知识可知点P到直线x-my-2=0的距离的最大值为点Q到直线x-my-2=0的距离1+|OB|，接下来，再让直线x-my-2=0进行“转动”，数形结合可知1+|OB|≤1+|OA|，所以当点B与点A重合，点Q与点D重合时，1+|OB|的最大值为3.所以当直线x-my-2=0的方程为x=2(此时m=0)，且点P为点D(-1，0)时，d的最大值为|AD|=3.故选择答案C．

点评根据单位圆与过定点的直线束之间的关系，依次在保持直线“静止”时让点P在单位圆上运动，再让直线“转动”起来，通过数形结合并利用平面几何的知识来转化与应用，进而数形结合得以确定相应的二元问题的最值．

其实，当我们破解完一道数学问题后，要加以不断总结，不断领悟反思，进而可以有效达到多角度切入，并能有效进行深度挖掘，进行有效深度学习，从而真正达到触类旁通、一题多解的效果，有助于培养数学科学的思维习惯，良好的核心素养以及能力素质．