模拟样机技术在轿车转向轮结构参数优化的应用

孙银银,唐 焱,唐荣江

(桂林电子科技大学机电工程学院，桂林 541004)

作为汽车重要总成之一的悬架系统，不仅影响车辆的操纵稳定程度，同时也决定着汽车高速行驶的安全性[1]。车辆在行驶的过程中车轮定位参数会随着车轮的受力和车身的运动而变化，同时定位参数的变化能反映悬架性能的优劣，因此，要求定位参数在合理变化的范围之内[2]。

文献[3]针对某一具体车型，通过测量获得实车参数，在ADAMS/car中进行了试验仿真，并利用insight模块对悬架相关参数进行正交化试验，提出了乘用车悬架性能的综合评价方法和评价指标，验证了基于ADAMS/car多体动力学建模的实用性。文献[4]进一步利用多体动力学仿真软件建立了麦弗逊悬架系统和双横臂悬架系统；对比分析了两种悬架系统的车轮定位、行驶稳定性等方面优缺点，并对系统前束值进行优化，提高了车辆的操纵稳定性。文献[5]通过建立前悬架刚形体模型，分析悬架针对主销内倾角的主要因素并对坐标参数进行了优化，使得悬架性能改善。但是前悬架的横摆臂是传递动态荷载的主要构件，在不同行驶工况下，横摆臂承载后会发生非线性弹性变形，导致车轮定位参数变化，传统设计及计算难以准确评估，因此获得能真实反映轿车行驶状态的前悬架刚柔耦合系统模型对提高车辆的操纵稳定性尤为重要。

介于汽车在行驶过程中横摆臂的非线性弹性形变，运用Hypermesh软件对悬架横摆臂作柔性处理，能获得真实反映轿车行驶状态的柔性体横摆臂模型，并替换在Adams/car环境建立的刚性前悬架横摆臂，生成前悬架刚柔耦合模型。以车轮垂直位移作控制量进行仿真试验，分析定位参数变化规律，明确优化目标并实施针对性优化处理，提高了车辆的行驶平顺性，降低轮胎的三维磨损。

1 目标车型前悬架系统模型

1.1 目标车型前麦氏悬架参数

剖析目标车型三维CATIA模型结构特点，确定前悬架硬点坐标如表1所示。采集和计算得到悬架基本参数，其中满载质量为1 420 kg、整备质量为 1 070 kg、轴距为2 385 mm、轮距为1 432 mm。

表1 硬点坐标Table 1 Hardpoints coordinates

1.2 麦氏悬架系统刚性模型

目标车型麦式前悬架主要结构包括转向节、下摆臂、螺旋弹簧、转向横拉杆、驱动半轴、上滑柱、轮毂、衬套、减震器等。进入Adams/car模板界面，根据目标车型实际结构及尺寸修改模型，并导入硬点坐标、质量、转动惯量等参数值，建立实体子系统模型。其中轮胎采用解析型UA模型，可兼顾纵向、侧向松弛效应，且所需计算参量较少，能够满足设计标准要求[6]。将前悬架子系统模型导入Adams/car转换到标准界，并按需求与系统试验台装配，建立仿真试验前悬架刚性体总成系统，如图1所示。

图1 前悬架刚性体总成模型Fig.1 Front suspension rigid assembly model

2 目标前悬架刚柔耦合模型建立

2.1 悬架横摆臂有限元模型建立和模态分析

在Hypermesh有限元软件中建立横摆臂三维模型并进行网格划分和参数的定义。遵循有限元网格划分相关标准和规则，设置横摆臂材料属性，弹性模量为211 000 N/mm，材料密度为7 800 kg/m3，泊松比为0.3，厚度为3.5 mm。将下摆臂设置为壳单元，网格划分总数为19 111个，横摆臂有限元模型如图2所示。

图2 横摆臂有限元模型Fig.2 Finite element model of lower-control arm

利用optistruct模块对生成的横摆臂有限元模型作模态分析，检验所建模型与实体构件的相符程度，由于未加载荷条件下前6阶模态频率趋向于零可忽略，试验仅考虑7～21阶模态频率测试[7]。综合考虑结构尺寸，精度需求等因素，进而确定试验边界条件，测试结果如表2所示。

对比目标车横摆臂理论模态频率数据，模型算数平均误差在5%之内，符合标准要求，所建横摆臂有限元模型用于仿真分析能准确反映系统实际结构特性。

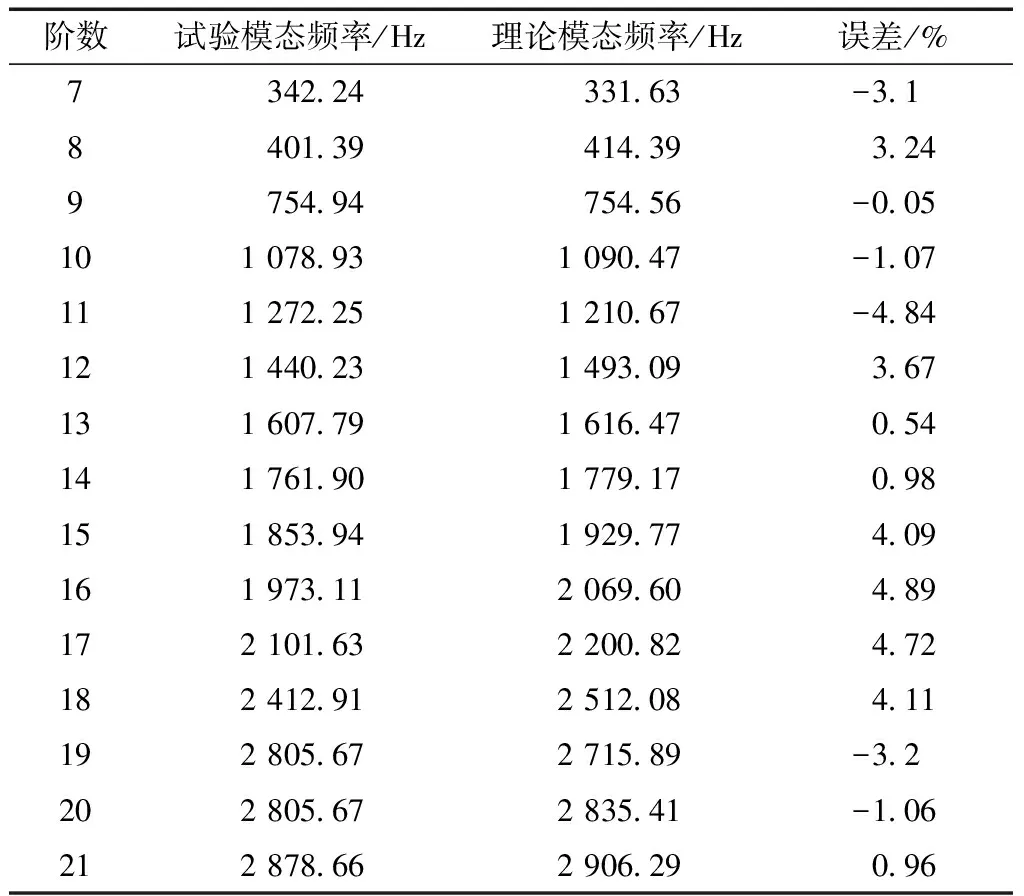
表2 横摆臂模态分析结果Table 2 The modal analysis result of lower-control arms

2.2 前悬架刚柔耦合系统

将Hypermesh软件中的模态分析结果信息另存为MNF格式文件，并导入Adams/car模块替换刚性模型中的横摆臂构件，生成刚柔耦合模型如图3所示。

图3 前悬架刚柔耦合模型Fig.3 Front suspension rigid-flexible coupling model

考虑横摆臂承载和柔度远大于其他机械结构件，对联合仿真实验作如下说明。

(1)除轮胎、橡胶衬套、阻尼及弹性元件外，忽略其他相关构件的尺寸、形状变量。

(2)忽略所有运动副相对运动的摩擦阻力。

(3)转向轮空载静态理想定位参数出厂标准如表3所示。

表3 静态车轮定位参数Table 3 Initial wheel positioning parameter

3 联合仿真试验及数据处理

3.1 试验设计

对前悬架刚柔耦合模型进行双轮同向激振试验仿真运行，仿真步数为50，轮中心垂直极限行程±50 mm。

3.2 数据处理及分析

运行ADAMS/car模块进入后处理模式，将仿真结果导入ADAMS/Processor模块，利用后处理模块处理功能即可获得目标函数仿真曲线。试验针对目标车型空载条件下转向轮前束、外倾、主销后倾、主销内倾、四大定位角参数作动态测量。

3.2.1 前束角动态测试及分析

前束角的理想设计为0°～1°，轿车系列前束角取值倾向偏下限，目标车型出厂标准0.023 6°。若因车轮跳动及横摆臂承载变形造成前束角变化过大，将导致车辆直线行驶能力下降，加速轮胎单侧磨损，并影响车辆操作稳定性[8]。

目标车型空载行驶试验前束角变化数据如图4所示。前束角变化曲线(图4)表明，在车轮跳动±50 mm 极限内，前束角动态绝对变化量为-0.227 8°～0.425 3°，表明目标车型前束角变化范围较大，有待作结构优化予以改善。根据试验假设可知，其主要影响因素是悬架自身特性和横摆臂变形，由于悬架自身特性影响整车性能不便轻易变动，因此基于理想前束角的优化处理应集中于横摆臂结构、方位、支撑点等相关结构参数配置。

图4 前束角变化曲线Fig.4 The curve of toe angle

3.2.2 外倾角动态测试及分析

等同条件下试验采集的外倾角动态数据如图5所示。曲线(图5)表明，转向轮在极限跳动行程内，外倾角动态绝对变化量为0.748 9°～-1.440 2°。参照静态车轮外倾角-0.358 2°，其相对变化量在标准要求±1°范围之内，其中承载增加时车轮下跳，外倾角向正方向变化，车轮侧向附着力有增加趋势，变化趋势合理。定性及定量分析表明，原型设计外倾角曲线变化范围过大，需进一步优化。

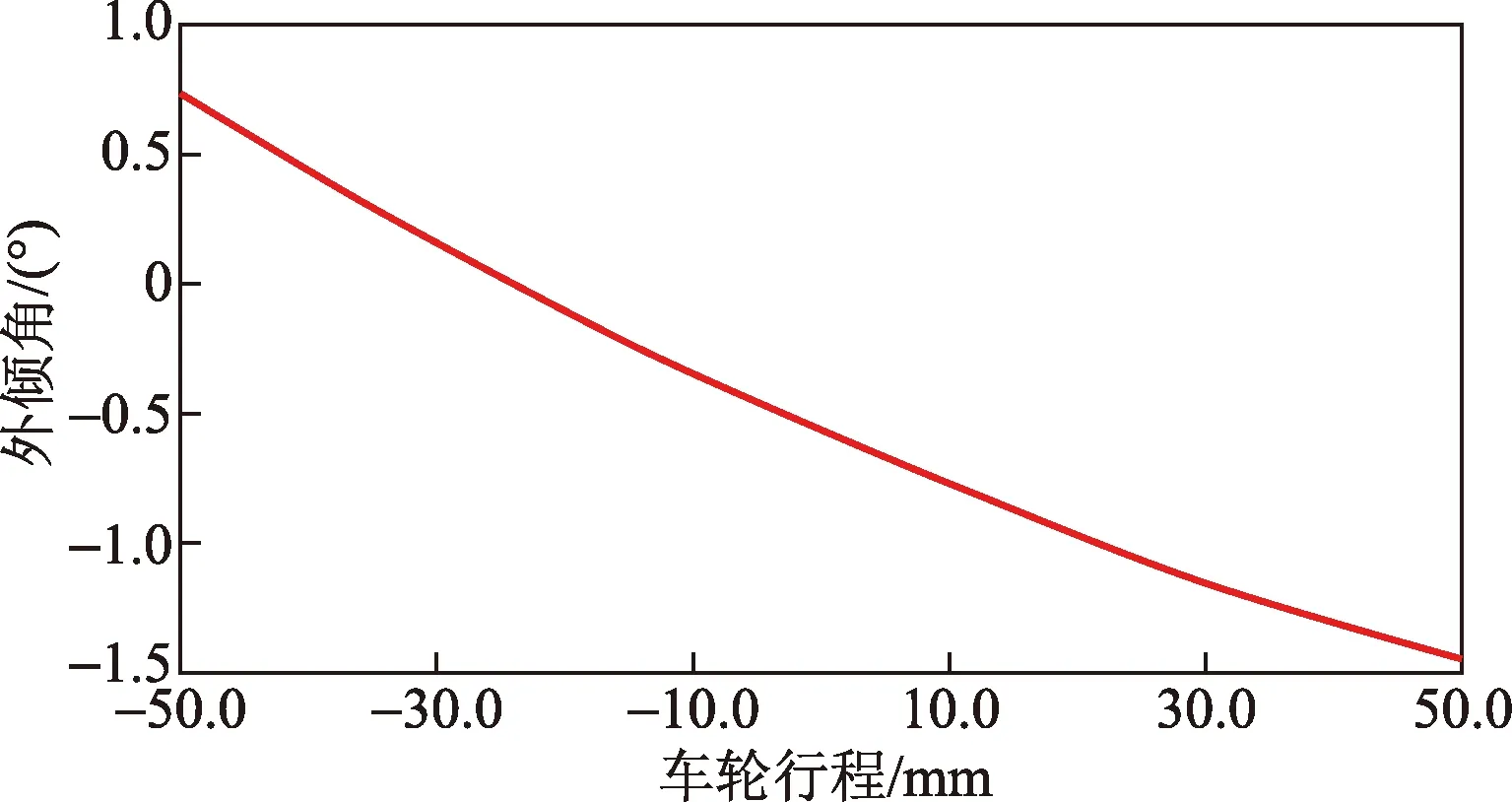
图5 外倾角变化曲线Fig.5 The curve of camber angle

3.2.3 主销后倾角动态测试及分析

目标车型空载理想主销后倾角2.731 1°，其数值及其变化是影响产生预期回正力矩的主要因素，仿真测试主销后倾角动态变化数据如图6所示。

图6 主销后倾角变化曲线Fig.6 The curve of caster angle

图6数据显示，在车轮中心垂直跳动极限范围内，主销后倾角变化范围为2.314 4°～3.337 6°，参照静平衡理想外倾角2.731 1°其变化范围在±0.5°左右。当轴荷减轻车轮上跳时，后倾角有逐渐增大趋势，能维持转向轮稳定的回正力矩，可见主销后倾角的曲线变化趋势合理，符合汽车设计相关技术标准。

3.2.4 主销内倾角动态测试及分析

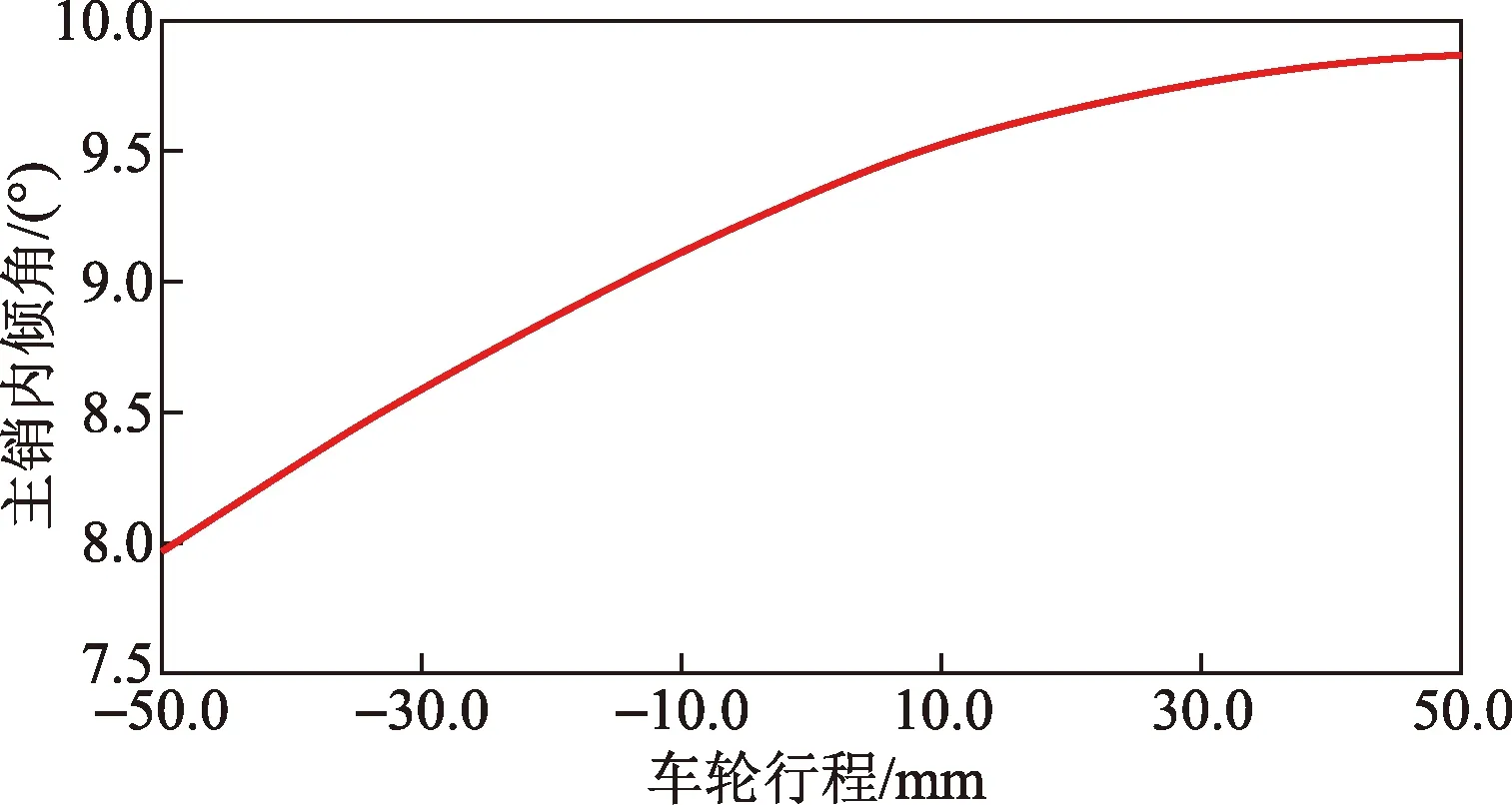
图7 主销内倾角变化曲线Fig.7 The curve of kingpin inclination angle

主销内倾角与车轮跳动关系仿真结果曲线如图7所示。主销内倾角变化曲线(图7)显示，静态主销内倾角9.334 9°，绝对量变化范围7.960 5°～9.864 4°，符合汽车设计主销内倾角7°～13°的规范，满足设计要求。当车轴加载车轮下跳，主销内倾角减小量较大，回正力矩相对稳定。当路面不平车轮剧烈跳动时，由于主销内倾角相对变化小于2°，其随时间变化率小，可保证车辆的操作稳定性。

4 外倾角与前束角的匹配优化

外倾角和前束角匹配不当在车辆行驶过程中会出现侧滑，行驶不稳定，加剧转向机构和轮胎的磨损。通过汽车侧滑检测试验台可以得到前束角与侧滑量之间的变化规律，利用测得试验数据回归分析得到测试目标车型前束角和外倾角最佳匹配值，根据该值数据对样车进行优化，并进行双侧轮同向激振仿真，得到优化对比数据。

4.1 汽车侧滑检测试验

试验采用SQJ-C型侧滑试验台，如图8所示，其精度为±0.2 m/km。HIS528双轴倾角传感器，精度为0.02°。

利用侧滑试验台测得前束值为-4、-2、0、2、4、6、10 mm时的车轮侧向滑移量，试验数据如表4所示。

图8 测量目标车型侧滑量Fig.8 Measuring the sideslip of a target vehicle

表4 前束值与侧滑量测试数据Table 4 The test data of wheel toed and sliding volume

4.2 试验结果分析

车辆在动态行驶过程中，侧滑量与前束角之间是非线性变化，只能通过建立数学模型来定量分析。设因变量为侧滑量，自变量为前束值。利用多项式回归法可近似逼近侧滑量和前束值的数学关系[9]。多项式回归数学模型如式(1)所示。

(1)

(2)

对回归方程进行显著性检验，即F检验，F又称为方差检验，由回归方差与剩余方差之比计算得到[9]。检验假设应用统计量F如式(3)所示：

(3)

式(3)中：U为侧滑量y的回归平方和，其自由度为m(m为自变量的个数)；Q为侧滑量y的剩余平方和，其自由度为n-m-1(n为试验观测次数)。

其中回归平方和U与剩余平方和Q相加即为总偏差平方和Syy，具体计算公式为

(4)

式(4)中各方程自由度的计算公式如式(5)所示：

(5)

式(5)中：df总为总偏差Syy的自由度，n=7为实验次数；df回为回归平方和U的自由度，m=2为自变量个数；df剩为剩余平方和Q的自由度。

对于给定置信度α，由分布表F可查Fα(m，n-m-1)的数值，如果F>Fα(m,n-m-1)，则m个自变量回归效果显著，经式(4)、式(5)计算得到显著性检验表如表5所示。

表5 方程显著性检验数值Table 5 The test value of equation significance

取检验水平α=0.01，查表得F0.01(2,4)=18.00，F=23.499 6。F>F0.01(2,4)，表明所建方程达到显著水平。

前面验证了回归方程中全部自变量的总体回归效果，但总体效果显著不能代表每个自变量对因变量是重要的，因此检验每个自变量是否显著，需要验证回归系数组成的系数向量C对响应变量是否有显著影响，偏回归平方和Uj与检验值F的理论计算公式如式(6)、式(7)所示[10]。

偏回归平方和：

(6)

式(6)中：bj为第j次项所对应的偏回归系数；cjj为回归系数向量C主对角线上的第j个元素；Uj为第j次项的回归平方和。

检验值F：

Fj=Uj/Qj，j=1,2,…，n

(7)

式(7)中：Qj为第j项的剩余回归平方和；Fj为第j次项的检验值。

经计算得到回归系数显著性检验的各项数值如表6所示。

表6 回归系数显著性检验表Table 6 The test of value regression coefficient significance

经查表F0.01(1,4)=21.20，得到一次分量F>F0.01(1,4)(F=31.364 1，F0.01(1,4)=21.20)，二次分量F>F0.01(1,4)(F=25.487 6，F0.01(1,4)=21.20)，即所建方程偏回归系数回归关系显著，所建数学模型能正确反应前束值与侧滑量之间的函数关系。

4.3 外倾角与前束角最佳匹配优化

在侧滑量为0时，轮胎磨损最小，车辆操纵稳定性也较好，因此令回归方程中侧滑量S=0，求解该工况下最佳前束值，求解得到前束值T=0.87 mm，经前束角与前束值之间的转换公式计算得到前束角为δ=0.067 2°。

由车轮外倾角和前束角的最佳平衡关系可计算得到最佳外倾角值，最佳匹配公式如式(8)所示[11]。

(8)

式(8)中：δ为前束角；γ为外倾角；D为转向轮前束测量值；l轮胎接地印迹长度；r为车轮滚动半径。

通过上式计算得到外倾角γ=-0.243 9°。通过调整模型前束角和外倾角并再次进行仿真分析，得到模型优化前后仿真分析曲线如图9、图10所示。

图9 优化前后前束角变化曲线Fig.9 Toe angle change curve before and after optimization

图10 优化前后外倾角变化曲线Fig.10 Camber angle change curve before and after Optimization

虚线显示优化后前束角变化范围为-0.162 3°～0.366 1°，相对结构优化前变化范围降低了19.09%。外倾角变化范围为0.612 4°～-0.702 2°,相对优化前变化范围降低了39.94%，该结果有利于提升车辆直线行驶性和操作稳定性，同时降低轮胎的磨损速率。

5 结论

在Adams/car环境建立和验证目标车型刚柔耦合前悬架模型，通过对模型的联合仿真分析得到以下结论。所建刚柔耦合模型符合实体承载及动态特征，试验结果能反映转向轮定位参数变化规律。双滑板侧滑试验获得侧滑量与前束值的函数关系，经过验证得到最佳前束值与外倾角的匹配关系，得到最佳匹配的前束角与外倾角，重新调整模型后，目标车型前束角变化降低19.09%，外倾角变化量降低39.94%。研究结果为复杂机械结构多目标优化设计提供了一种有效的方法。