Exact solution of free vibration of adjacent buildings interconnected by visco-elastic dampers
2020-06-06YongChenZugungYingGuohuiShen
Yong Chen, Zugung Ying, Guohui Shen,*
a Department of Civil Engineering, Zhejiang University, Hangzhou 310058, China
b Department of Mechanics, Zhejiang University, Hangzhou 310027, China
Keywords:Flexible high-rise coupled building system Non-dimensional motion equation Free vibration Exact complex mode shape
ABSTRACT With consideration of a high-rise coupled building system, a flexible beams-based analytical model is setup to characterize the dynamic behavior of the system. The general motion equation for the two beams interconnected by multiple viscous/visco-elastic dampers is rewritten into a non-dimensional form to identify the minimal set of parameters governing the dynamic characteristics. The corresponding exact solution suitable for arbitrary boundary conditions is presented. Furthermore, the methodology for computing the coefficients of the modal shape function is proposed. As an example, the explicit expression of the modal shape function is derived, provided only one damper is adopted to connect the adjacent buildings. Finally, to validate the proposed methodologies, three case studies are performed, in which the existence of the overdamping and the optimal damping coefficient are revealed. In the case of using one damper in connecting two similar buildings, the estimating equations for the first modal damping ratio are formulated.
The structural damping plays an important role in the vibration of the structure subjected to time-varying loadings, such as wind loading [1, 2], earthquake loading. Nevertheless, there are evidences that the intrinsic damping of the tall buildings decreases with the increase of the height [3]. As a low damping leads to an adverse large amplitude vibration of the structure,using external damping devices or vibration absorbers [4] to suppress the vibration, then to ensure the safety of the structures has gained great attention. Besides, connecting two adjacent buildings together to attenuate the structural vibration has been an active research field in recent decades, and it can be traced back to the work in 1972 by Klein et al. [5].
Previous studies have shown that the vibration of the interconnected adjacent structures can be effectively mitigated by applying the passive energy dissipation devices [6-23], active[15, 20, 24-29] and semi-active [19, 30-35] control strategies to the connectors. Among these methods, the use of the viscous/visco-elastic dampers has attracted extensive attention because of its easy installation and almost free maintenance.Considering two buildings interconnected by viscous dampers that are uniformly distributed over the height of the shorter building, Luco and De Barros [6] determined the optimal values of the damping, along with the optimum height of the shorter building to minimize the response of the taller building, through an investigation of a system consisting of two uniform shear beams. Using discrete visco-elastic dampers, Xu et al. [7] surveyed the dynamic response of the damper-connected adjacent buildings trough pseudo-excitation algorithm. To achieve a more accurate random seismic response of such a non-classically damped system in the frequency domain, Zhang and Xu [8]developed a combined method for analysis, i.e. the combination of the pseudo-excitation algorithm and the complex modal superposition. Given that only one damper is installed at the top of the shorter building to connect the buildings, Christenson et al.[15] examined the overall performance of the system and compared the efficiency of the passive and active coupled building controls for flexible structures, by modelling the buildings as two cantilever beams and using the Galerkin method. Zhu et al. [17]modelled two adjacent structures as two multi-degree-of-freedom (2-MDOF) systems. Then, a reduced-order model incorporating two single-degree-of-freedom (2-SDOF) systems was attained via shape functions, and the corresponding formulas for computing the optimal stiffness and damping coefficients are presented. For the combined damper location and coefficient selection problem, Bigdeli et al. [18] developed a global search program. It was found that increasing the number of dampers does not necessarily improve the efficiency of the system, if the dampers have the same coefficient. Recently, after removing the assumption of equal damping coefficients, Bigdel et al. [22]found that increasing the number of dampers no longer exacerbates the dynamic behaviour of the system, by using a newly developed bi-level optimization procedure. Considering two linear elastic shear cantilever beams interconnected by a viscous/visco-elastic damper at the top of the shorter building,Tubaldi [21] derived the approximate expressions for the damping ratios of the first two fundamental vibration modes in the case of low added damping, by utilizing assumed mode method.
In previous studies, the shear beams were conventionally employed for modelling the multi-storey buildings. Nevertheless, for the flexible high-rise coupled building system, the relevant study based on the flexural continuous beams-based analytical modelling remains insufficient. This work aims to provide the exact analytical mode shapes, as well as the exact frequency equation of the flexible high-rise coupled buildings connected by multiple viscous/visco-elastic dampers. Firstly, analytical modelling is performed by using the Bernoulli-Euler beam, and a non-dimensional model is derived to identify the minimal set of parameters governing the dynamic characteristics. Then, the exact solution suitable for arbitrary boundary conditions is presented, which results in a frequency equation of the system.Whereby, the exact analytical mode shape is formulated. Finally,to validate the proposed methodologies, three case studies, focusing on the complex mode shape, evolution of the pseudoundamped natural frequency, and modal damping ratio respectively, are performed. In addition, in the case of using one damper to connect two similar buildings, the estimating equations for the modal damping ratio of the first mode are presented.
An idealized system shown in Fig. 1 is setup for analysis, and the system consists of two uniform Bernoulli-Euler beams and connectors. Both of the beams are fixed at the ground. Without loss of generality, the lengths of the beams are l1and l2≤l1respectively. The Cartesian coordinate system is employed to describe the beam vibration, and x coordinate is set along the beam and the origin is set at the clamped end. As shown in Fig. 1,y1denotes the lateral time-varying displacement of the taller beam undergoing vibration, and y2denotes the lateral timevarying displacement of the shorter beam. The bending stiffness is characterized by EI, in which E is the Young's modulus and I is the area moment of inertia of cross-section about neutral axis.The mass per unit length is denoted by m. The subscripts ‘1’ for the taller beam and ‘2’ for the shorter beam are utilized to distinguish the physical parameters of the taller beam from that of the shorter beam, as shown in Fig. 1. Each connector comprises a linear viscous damper whose damping coefficient is denoted by Cd, and a linear spring whose stiffness is denoted by Kd. The distance from the clamped end to the location of the ith connector is denoted as ai. For convenience, the intrinsic structural damping of the beams is excluded herein.
According to D'Alembert's principle, the governing equation of the motion of the system can be formed as two partial differential equations, i.e.
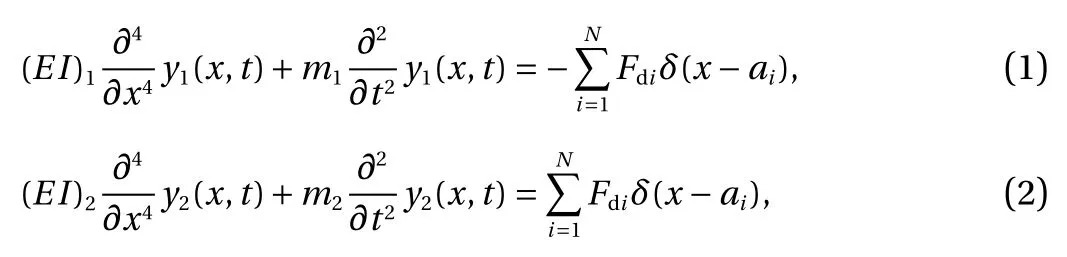
in which Fdiis the internal force of the ith connector and can be computed by
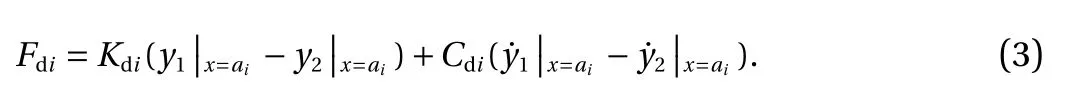
The system can be nondimensionalized by [36]
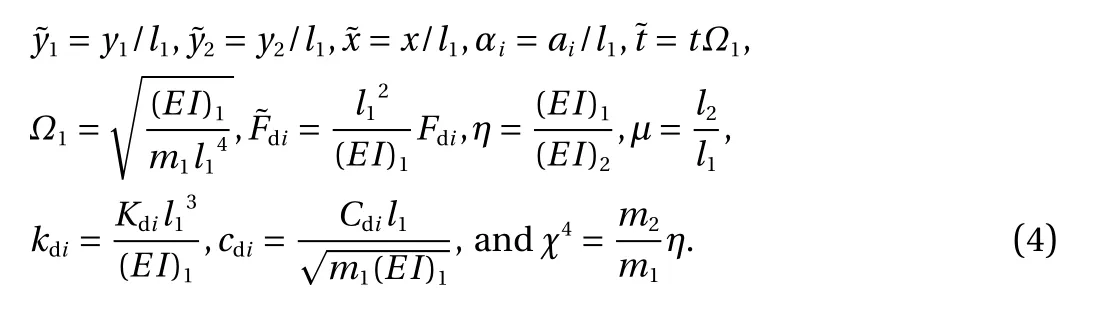
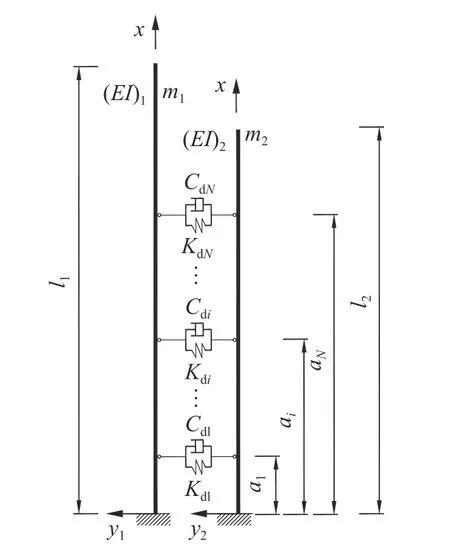
Fig. 1. Scheme of the system.
Thus, one obtains
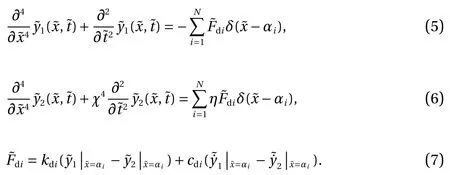
By using separation of variable, the motion of the system has a form of


For a linear system in a free vibration, the internal forces in the connectors have the same vibration frequency. Accordingly,the internal force of the ith connector has a form of [36]


where λ is the wave number, and can be computed by

And the exact solution of Eq. (12) can be expressed as [36, 37]
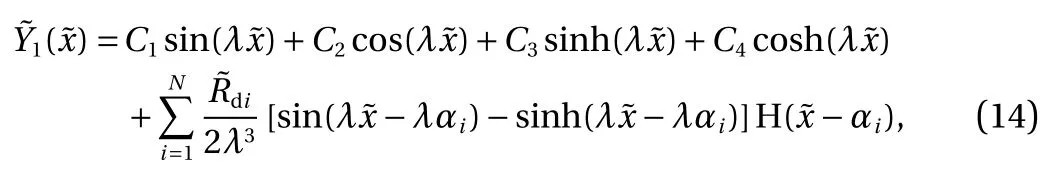
where Cn, n=1,2,···,4 are the coefficients that can be determined by using the boundary conditions of the taller beam.
In similar fashion, substitution of Eqs. (9) and (11) into Eq.(6) leads to
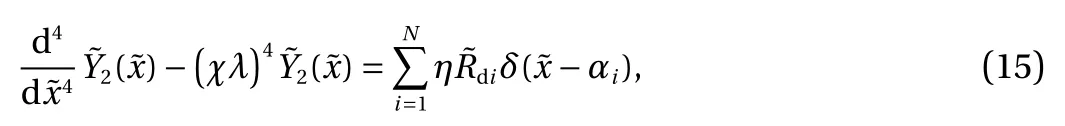
with an exact solution of

where Dn, n=1,2,···,4 are the coefficients that can be determined via the boundary conditions of the shorter beam.
It is worth noting that Eq. (14) and Eq. (16) are suitable for the beams with arbitrary boundary conditions. For the problem stated herein, the boundary conditions of the beams can be expressed as
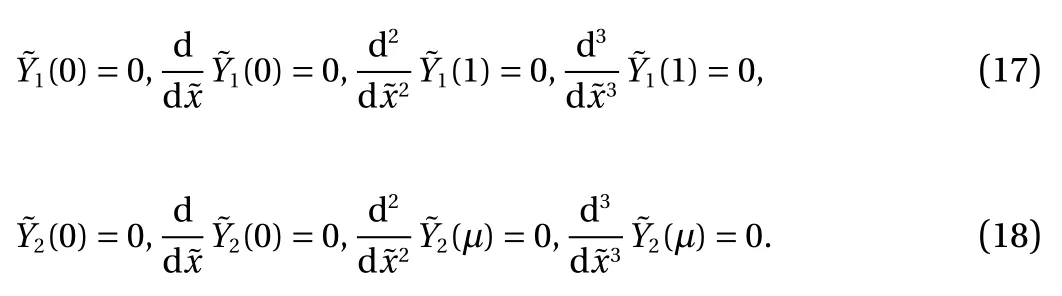
According to the virtual boundary condition method (VBCM)developed by Chen et al. [36], the balance of the forces on the ith connector with a form of
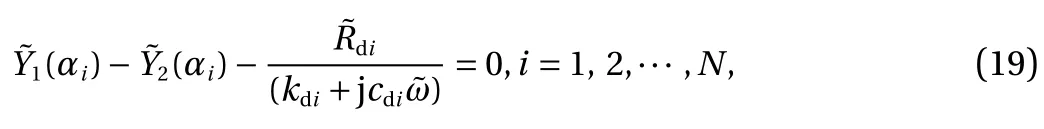
can be regarded as an virtual boundary condition. Thus, by applying the boundary conditions, one obtains

where G is the vector of the undetermined coefficients and expressed as

in which the superscript ‘T’ denotes the transpose operation.The matrix A in Eq. (20) can be thus formed as

where
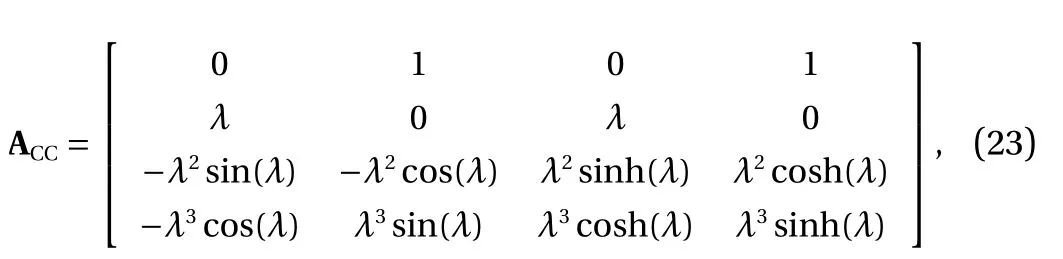
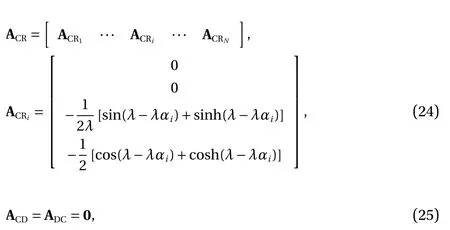

Thus, the nontrivial solution of the coefficient vector requires [36, 37]

Equation (32) is essentially the characteristic equation (frequency equation) of the whole system. The roots of the equation can be easily converted into the complex-valued natural frequencies of the system via Eq. (13). The real part ofrepresents the decaying ratio of a free vibration, whereas the imaginary part represents the frequency of the periodic vibration. Eq.(32) is a type of complex-valued transcendental equation, and could be solved through the argument principle method (APM)[36-38], or optimization method with an appropriately constructed objective function [39]. It is noted that the pole point,,(i =1,2,···, N), which is expressed as

needs to be excluded in finding the roots of Eq. (32).
It is convenient to obtain the mode shape of the connected structures by setting one of the entries in C to be 1.0. For example, let C1be equal to 1.0. Then, one may obtain a matrix that results from deleting the first row and the first column of A, i.e.A'. For the ith natural circular frequency,, that results from solving Eq. (20), the coefficients in Eqs. (14) and (16) can be obtained by

where G′results from deleting the first row of G, and P is the vector formed by the first column of the matrix that results from deleting the first row of A. By substitution of Eq. (34) into Eqs.(14) and (16), the ith mode shape can be therefore obtained.
For example, considering only one connector is employed,one may setto be 1.0. Then, Eq. (20) yields
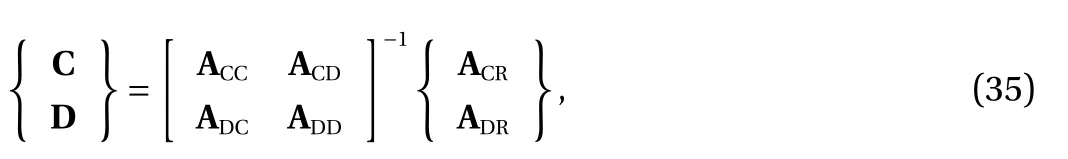
where
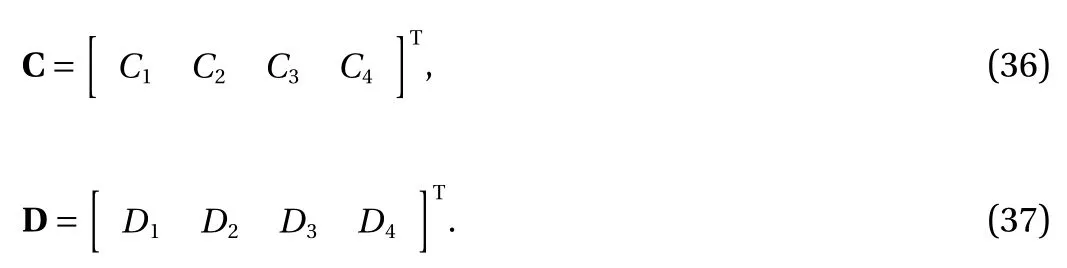
Thus, one has

and

In the follows, we firstly introduced two representative examples for the application of the proposed methodology. Then,the empirical equations, for the estimation of the modal damping ratio of the first mode, are presented in the third case study.
Consider two buildings with two connectors, having the nondimensional parameters of η=0.8 , χ=0.8, μ=0.8, α1=0.4,α2=0.8, kd1=1.0, cd1=0.8, and kd2=1.0. Varying the damping coefficient of the second damper, cd2, leads to the root loci of the natural circular frequencies, as shown in Fig. 2. The arrows in the figure show the directions of the loci with the increase of the damping. In Fig. 2, it could be clearly identified that the second modal vibration will be overdamped, as the damping increases.For the first and fourth modal vibration, there exists an optimal damping coefficient, which maximizes the corresponding modal damping ratio. Table 1 lists the selected natural circular frequencies for the different damping coefficients of the second damper.
In the second example, only one connector is considered.T he non-dimensional parameters adopted are η=0.8, χ=0.8,μ=0.8, α1=0.8, cd1=0.8, and kd1=1.0. Thus, the values of the first four wave numbers that are obtained by solving the frequency equation are λ1=2.0117+0.1407j, λ2=2.8352+0.7592j,λ3=4.6938+0.0007j, and λ4=7.3021+0.2703j respectively. Substituting these wave numbers into Eqs. (38) to (45) results in the corresponding mode shapes of the system. Figure 3 illustrates the real and imaginary parts of the first four mode shapes. The mode shapes of each beam are normalized by the maximum absolute value of the first mode of the beam. It is found that the first and the third modal vibrations are predominately the vibration of the taller beam, whereas the second and the fourth modal vibrations are mainly the vibration of the shorter beam. Since the imaginary parts of the modes are not ignorable, as shown in Fig. 3, which implies the non-constant configuration of the modal vibration.
In the third example, two similar buildings with a connector of a viscous damper is considered, which means η =1.0 , χ =1.0,and kd1=0.0. Note that the presence of the link stiffness serves mainly to shift the natural frequencies of the system [15], and hinders the vibration mitigation by connecting the structures [6].Therefore, a viscous damper rather than a visco-elastic damper is adopted herein.
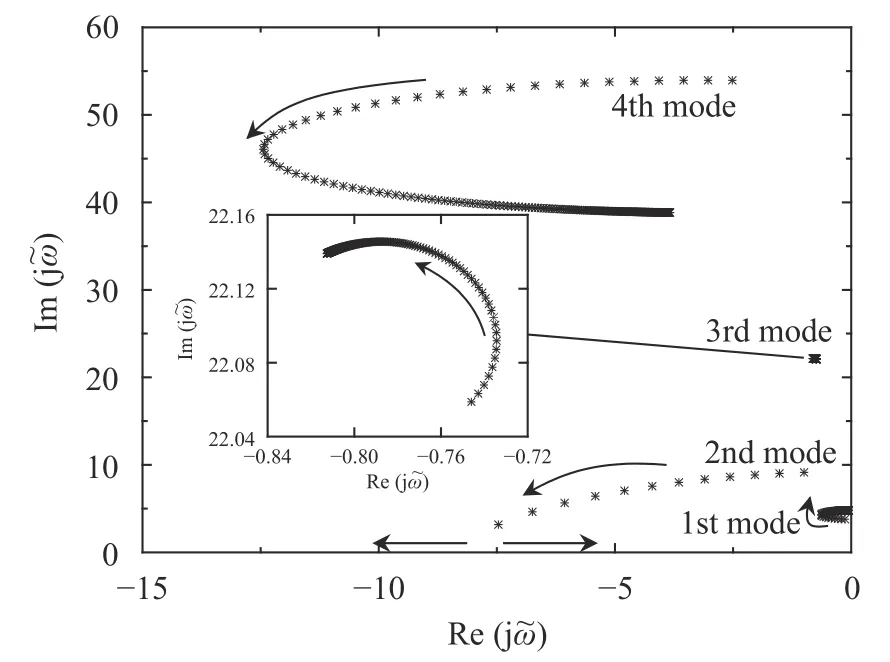
Fig. 2. Root loci of.
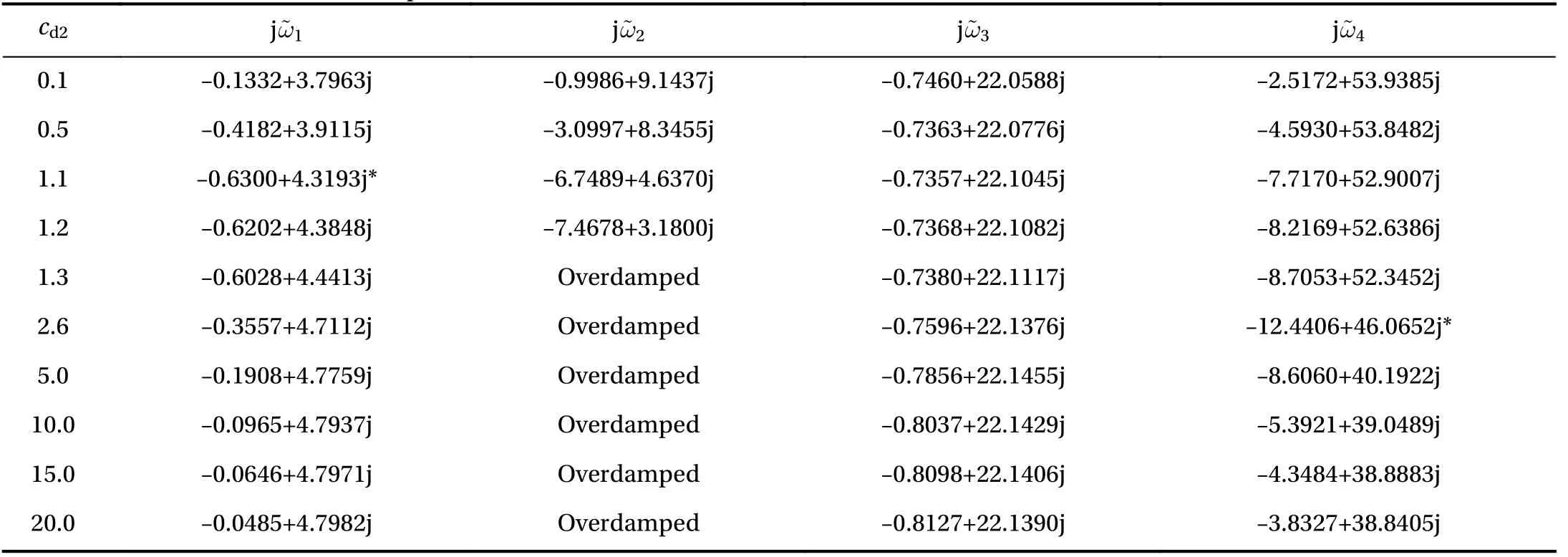
Table 1 Selected natural circular frequencies
For the interconnected two identical buildings (twin buildings), i.e. the building height ratio, μ, is equal to 1.0, it can be easily concluded from the frequency equation that the natural circular frequencies of a cantilever beam are also the solution of the frequency equation of the system, and the mode shapes of the cantilever beam are also the mode shapes of the system. In this situation, the two buildings vibrate in a similar fashion. The relative displacements between the buildings are zero, which leads to no energy dissipated by the damper, and then a zero additional damping. The relatively lower effectiveness of the damper connecting twin buildings [15] might be attributed to this.
Nonetheless, the damper remains functional. For convenience, the solutions that are the same as that of a cantilever beam are excluded in this discussion. Figure 4 illustrates the other solutions of the frequency equation. The non-zero imaginary part of theclearly indicates the effectiveness of the damper. It is worth noting that the root loci shown in Fig. 4 start from the natural frequencies of a cantilever beam individually. Furthermore, if the height of the damper exceeds a critical height, the first modal vibration is overdamped for a sufficiently large damping. Contrarily, the second modal vibration changes to be not overdamped.
A natural circular frequency for the underdamped vibration has a form of

in which the non-negative real-valued ξ represents the modal damping ratio, and the positive real-valuedis the pseudoundamped natural circular frequency [40]. Therefore, Eq.(46) yields

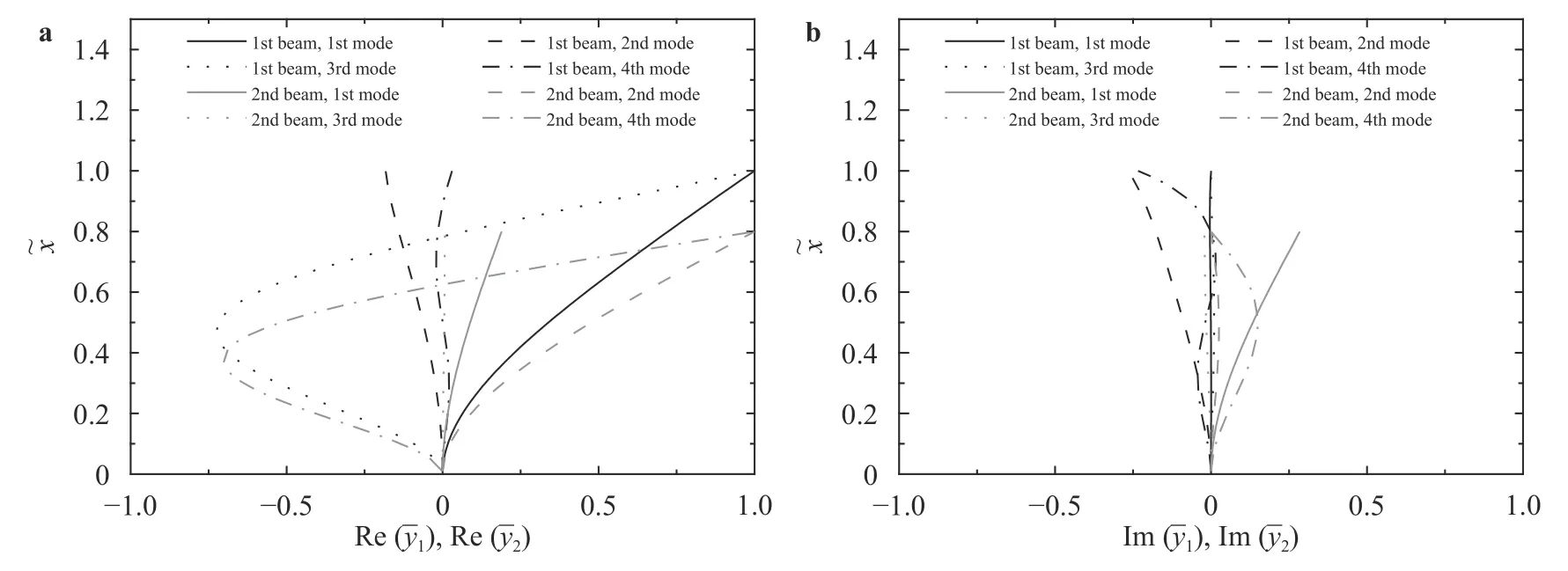
Fig. 3. Real and imaginary parts of the first four normalized mode shapes: a real part; b imaginary part.
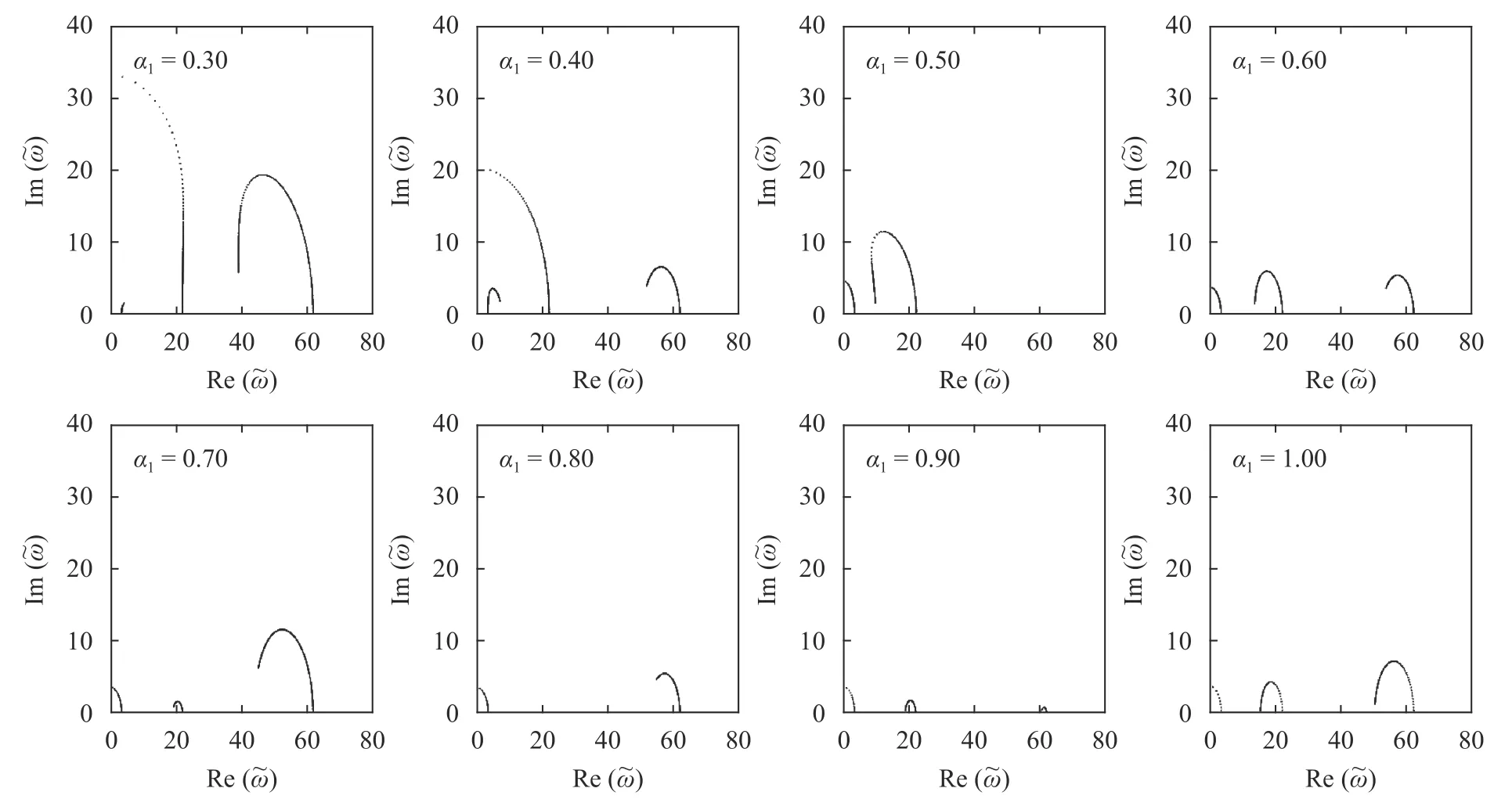
Fig. 4. Twin buildings: root loci of.

Figure 5 illustrates the first modal damping ratio varying with the damper's damping and location, where the estimated results marked by ‘×’ are the values computed by an empirical estimating equation, which will be introduced below. In the figure, it can also be found that the damping ratio will continually increase and finally exceed 1.0, if the location of the damper is high enough. In the cases of the lower locations, the optimal damping coefficient which maximizes the modal damping ratio can be identified.
Figure 6 shows the variation of the maximum modal damping ratio, along with the corresponding optimal damping coefficients. In the figure, the maximum damping ratios that are for the overdamped modal vibrations are set to be 1.0 for convenience of illustration. For the analysis on the overdamped modal vibration, one may refer to the work by Chen et al. [37]. Correspondingly, the optimal damping coefficient that corresponds to a damping ration of 1.0 is the value that the modal vibration will be overdamped if the damping coefficient exceeds it. It is found that the optimal damping coefficient decreases with the increase of the height of the damper, which indicates that the efficiency of the suppression of the first modal vibration can be improved by increasing the damper's height. In Fig. 6b, one may find one peak for the second mode, and two peaks for the third mode, and these peaks indicates the variation of the efficiency of the damper in suppressing either the second or the third modal vibration. Overall, if only one damper is involved, installing it at the top of the buildings seems to be the most efficient means, for suppressing the first three modal vibrations simultaneously.
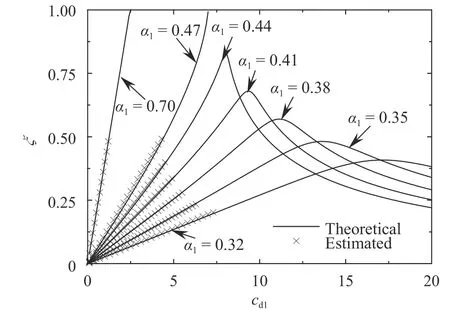
Fig. 5. Twin buildings: modal damping ratio of the first mode.
For convenience of application, the follows present the empirical estimating equations for the modal damping ratio of the first mode, on condition that there is only one damper used to connect the two similar buildings.
(1) μ=l2/l1=1.0

where

(2) μ=l2/l1<1.0
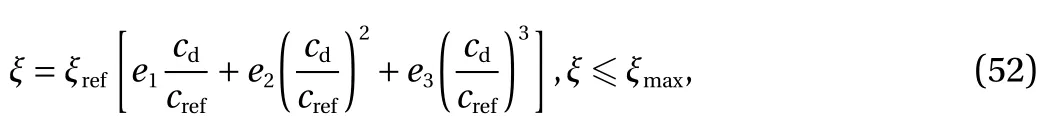
where
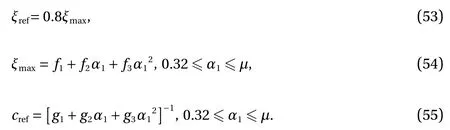
The coefficients, ei, fi, and giin Eqs. (52), (54) and (55),where i =1,2,3, vary with the building height ratio. Table 2 lists the values of the coefficients. For μ =1.0, Fig. 5 shows the theoretical damping ratios obtained via solving frequency equation,and the estimated damping ratios via Eq. (49). Moreover, for μ=0.6, the comparison of theoretical results and the estimations that are obtained through Eq. (52) are shown in Fig. 7. For the maximum modal damping ratio, the estimated results via Eq.(54) are compared with the results that are obtained by solving frequency equation, as shown in Fig. 8. A good agreement can be observed from these figures, which validates the proposed empirical equations.
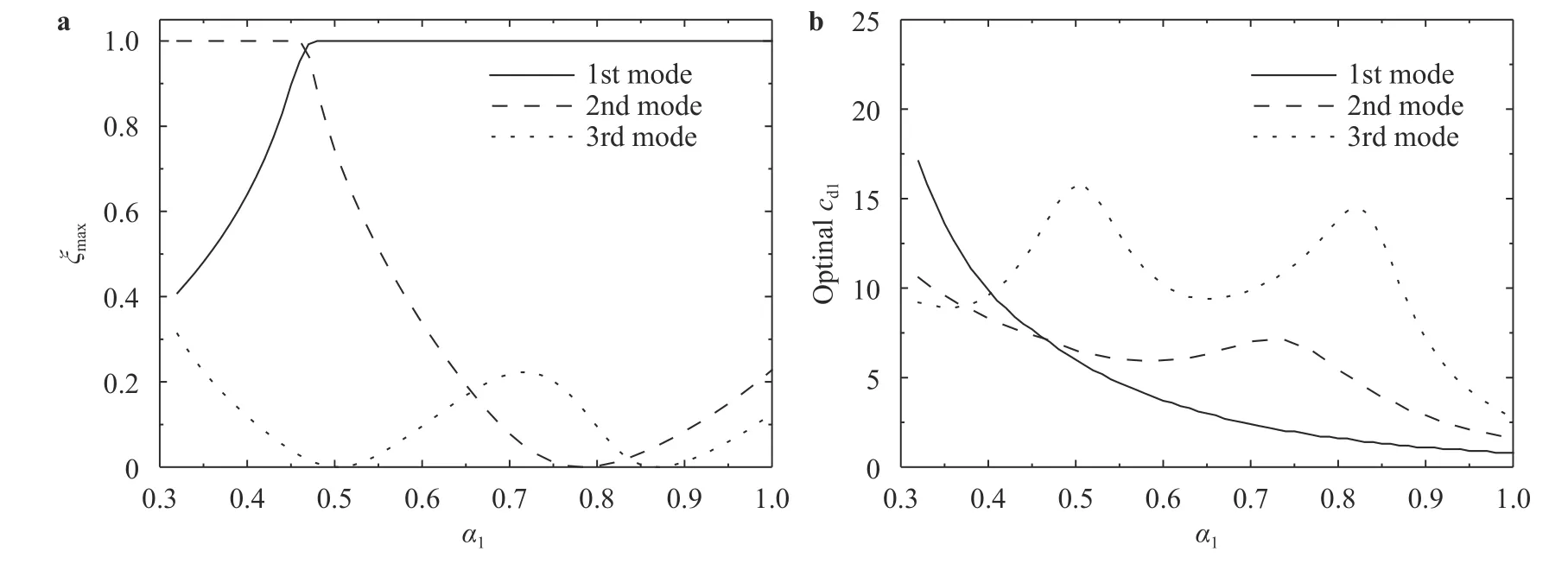
Fig. 6. Twin buildings: a maximum modal damping ratio; b optimal damping coefficient.
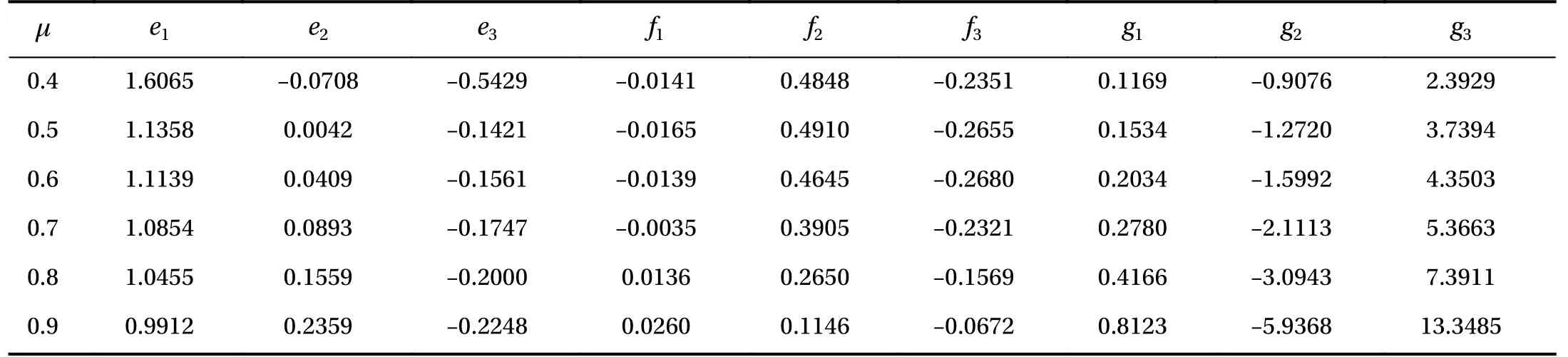
Table 2 Coefficients in Eqs. (52), (54), and (55) for different building height ratios
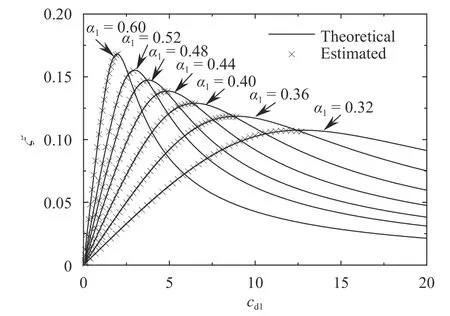
Fig. 7. Modal damping ratio varied with damping and location().
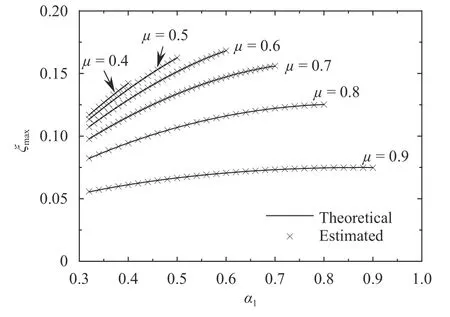
Fig. 8. Maximum modal damping ratio varied with building height ratio and damper's location.
For the two adjacent buildings interconnected by multiple visco-elastic dampers, the analytical modelling and solution are investigated to gain insight into the dynamic characteristic of the system. The exact solution derived is also suitable for arbitrary boundary conditions. Moreover, for the problem stated herein,the frequency equation, and the methodology for attaining an exact analytical mode shape are proposed. In the case of using one visco-elastic damper, the explicit analytical expression of the mode shape is given. Three representative examples are introduced to clarify the application of the proposed method. In the case of the two similar buildings interconnected by one viscous damper, empirical estimating equations for the modal damping ratio of the first mode are proposed, and validated by the exact theoretical results.
杂志排行
Theoretical & Applied Mechanics Letters的其它文章
- Editorial: Computational granular mechanics
- Construction of irregular particles with superquadric equation in DEM
- Prediction on dispersion in elastoplastic unsaturated granular media
- A block particle coupled model and its application to landslides
- Modified virtual internal bond model based on deformable Voronoi particles
- Modeling of deformation processes in rock massif in the vicinity of underground goafs considering the formation of discontinuity zones
