Prediction on dispersion in elastoplastic unsaturated granular media
2020-06-06ChenxiXiuXihuChuJioWng
Chenxi Xiu, Xihu Chu,b,*, Jio Wng
a School of Civil Engineering, Wuhan University, Wuhan 430072, China
b State Key Laboratory for Structural Analysis of Industrial Equipment, Dalian University of Technology, Dalian 116024, China
Keywords:Unsaturated granular media Elastic-plasticity Cosserat Wave propagation Dispersion
ABSTRACT This study focuses on the propagation of the plane wave in the elastoplastic unsaturated granular media, and the wave equations and dispersion equations are derived for the media under the framework of Cosserat theory. Due to symmetry, five different wave modes are considered and predicted for the elastoplastic unsaturated granular media based on the Cosserat theory, including two longitudinal waves, one rotational longitudinal wave and two coupled transverse-rotational transverse waves. The correspondence is discussed between these Cosserat wave modes and the classical wave modes. Based on the dispersion equations, the dispersion behaviors are obtained for the five Cosserat wave modes. The results indicated that the different stress-strain stages,including the elastic, hardening and softening stages, have obvious effect on the dispersion behaviors of the Cosserat wave modes.
Granular media are typical porous materials composed of a solid skeleton and pores, and the pores are typically filled with a fluid (liquid or gas). Dynamic analysis of this media is an important subject in the fields of seismology, soil mechanics, mechanical, civil and aerospace engineering, etc. Typically, Biot [1, 2]first studied the propagation of elastic wave in liquid-saturated porous solids. Owning to viscous coupling between the solid skeleton and the pore fluid of granular media, the response to pulse loading is generally dispersive [3]. Previous studies [4-7]investigated the dispersion of the wave propagation in typical saturated granular media. Li et al. [3] proposed a model based on the Biot theory for simulating coupled hydro-dynamic behavior in inelastic unsaturated porous media and investigated dispersion of wave propagation in the media.
However, granular media typically have complex microstructures generally regarded as discrete particle assemblies at the micro scale. From the physical essence's perspective, the rotation of a material point should be considered, and researchers have reported the experimental observation of coupled rotational-translational wave modes in a non-cohesive granular phononic crystal [8]. However, the classical continuum theory of elasticity fails to exhibit the behavior of materials possessing microstructure, and it lacks the degree of freedom (DOF) for rotation, and consequently, the rotational wave cannot be predicted.Therefore, it is important to use an appropriate continuum theory to describe the physical essence of granular media. The Cosserat theory [9] defines six DOFs for each material point,where three additional DOFs correspond to rotations. This theory predicts a contribution of rotations to the dispersion of the shear elastic wave velocity as well as the existence of additional rotational wave modes [10]. And the rotational wave modes in the Cosserat media are proved to be an actual existence by experiments [11]. Therefore, the use of Cosserat theory is appropriate to analyze the dynamic problems for the granular media.
This study extends the work of Li et al. [3] under the framework of classical theory to the framework of Cosserat theory.Then, the wave equations and dispersion equations are derived for the elastoplastic unsaturated granular media based on the Cosserat theory, and the dispersion behaviors are predicted accordingly.
In the Cosserat theory, the geometric equations are expressed as [9]

where εijand κijare strain and curvature, respectively. And the constitutive equations are written as

And our previous study [12] introduced an extended Drucker-Prager yield criterion to describe the plastic behavior of granular media based on the Cosserat theory and derived the elastoplastic constitutive relationship of the Cosserat solid skeleton expressed as follow

where Depis the consistent elastoplastic tangent modulus matrix and its detailed operation is presented in Ref. [12].
With the introduction of momentum moment conservation equation in the Cosserat theory, the equilibrium governing equations for the Cosserat solid skeleton and the pore fluid can be written as [3, 13]
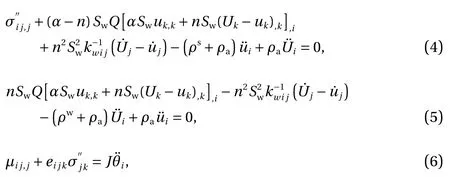

Considering the propagation of this plane wave along x1axis,we suppose the kinematic measures as
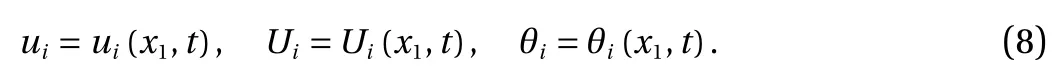
Therefore, wave equations can be obtained by substituting Eq.(8) into Eqs. (4)-(6). The solutions of the wave equations are given as following harmonic wave forms:
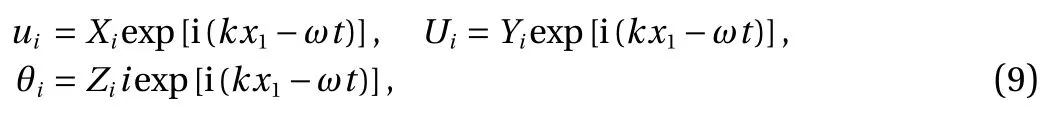
where k is the wave number, ω is the circular frequency, and Ai,Bi, Cidonate wave amplitudes. For simplification, the subscripts of Cijkland Bijklcan be defined as 11→1, 22→2, 33→3, 12→4, 21→5,31→6, 13→7, 23→8, 32→9, referring to the Voigt notation and our previous work [12].
Therefore, the waves equations can be divided into three groups as follows A: associated with x1direction
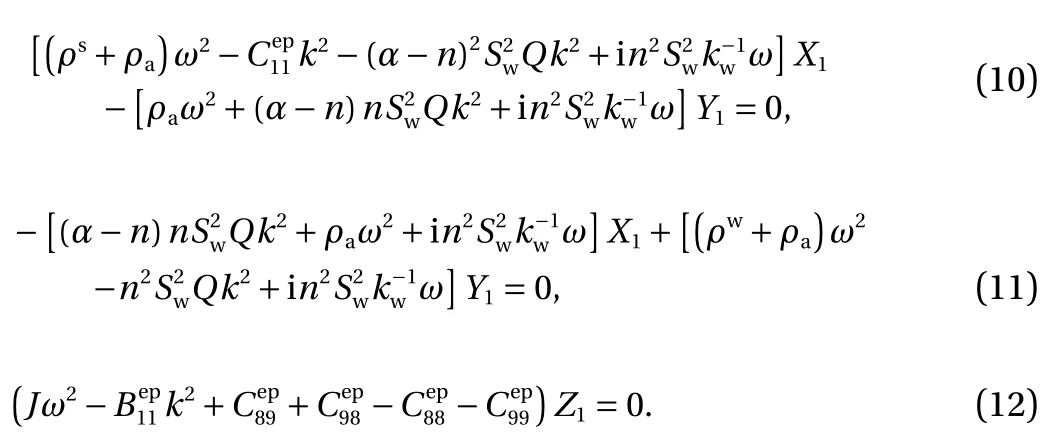
B: not associated with x1direction
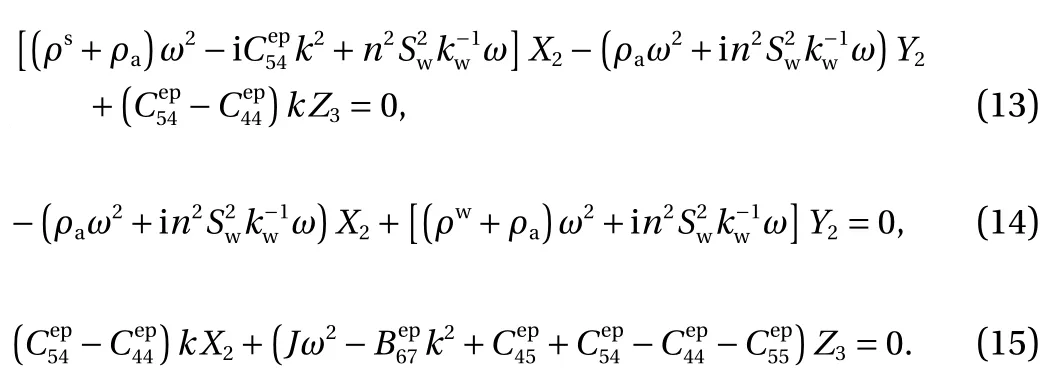
C: not associated with x1direction
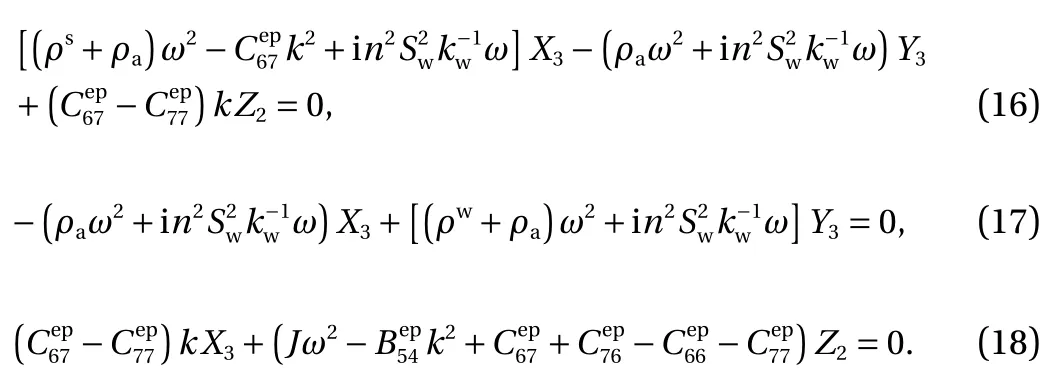
It is noteworthy that group B and group C are identical, because the plane wave is along x1direction leading to symmetric subscripts 2 and 3. In order to make these equations have nonzero solutions, their determinants should be zero. Therefore,the dispersion equations are obtained relating the frequency ω to the wave number k as follows A:

where
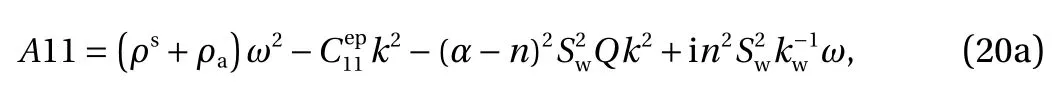
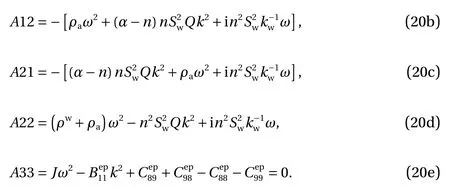
B or C:

where
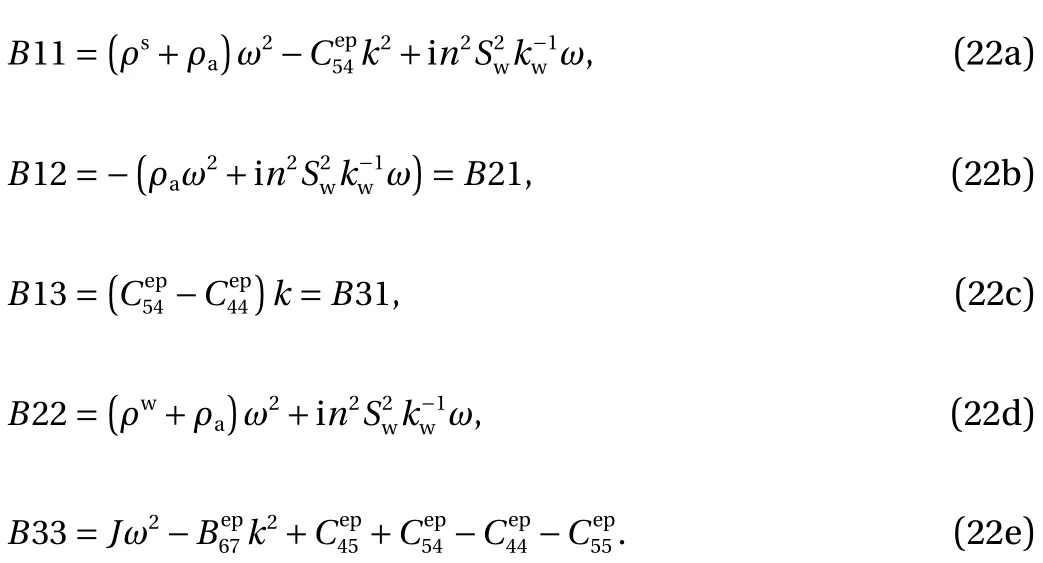
It is noteworthy that the wave number k should be complex to make the dispersion equations satisfied when the frequency ω is real. And k can be written as

where kris the real wave number, and β is a parameter representing amplitude attenuation.
Group A can predict two wave modes corresponding to a longitudinal wave and a rotational longitudinal wave respectively. The longitudinal wave can be called as the P wave with two solutions corresponding to P1 and P2 waves, and the rotational longitudinal wave can be called as the R wave. From group B, a transverse-rotational transverse wave mode is predicted, which can be called as an S wave, and the dispersion equation is quadruplicate, so it has two positive solutions corresponding to S1 and S2 waves respectively. For group C, another S1 and S2 waves are also predicted, and they are identical with those in group B,due to symmetry. Therefore, five wave modes are predicted and reduced from seven waves. It is noteworthy that the wave modes can be reduced to those in Ref. [14], when the granular medium is considered to be elastic and fluid-saturated.
Three stress-strain stages are investigated, including an elastic stage and two plastic stages corresponding to a hardening stage and a softening stage respectively, and the parameters are shown as Table 1. Therefore, the dispersion behaviors of different wave modes can be obtained for different stress-strain stages.
Figures 1 and 2 show dispersion and attenuation curves of P and S waves at different stress-strain stages: elastic stage, plastic stage 1 and plastic stage 2, respectively. As we can see, obvious dispersion behaviors are predicted for P1 wave, while no dispersion behaviors are predicted for P2 wave. The degree of dispersion behavior is higher with higher degree of plasticity for P1 wave. In Fig. 2, the attenuation for P1 wave is almost 80 times larger than that for P2 wave, and the wave speed vp=ω/krfor P1 wave is smaller than that for P2 wave (see slopes of curves in Fig. 1). It is noteworthy that the longitudinal waves correspond to movements where the skeleton and the fluid move in phase or in phase opposition, and the wave is called as a longitudinal slow wave which reflects the movement in phase opposition with larger viscous damping, consequently, the obvious dispersion and the lower wave speed [3]. Therefore, the P1 wave mode should correspond to the longitudinal slow wave or so-called Blot's wave. And with the increase of the degree of plasticity, the degree of attenuation for P1 wave increases, while the plasticity has slight effect on attenuation for P2 wave. Similarly, obvious dispersion behaviors are predicted for S1 wave, while slight dispersion behaviors are predicted for S2 wave. However, there is a special phenomenon that inverted change for the state of dispersion behaviors happen for both S1 and S2 waves at the softening stage (see the blue lines with diamond symbols in Fig. 1b). Because the S1 and S2 waves are related to the translation-rotation DOFs, it can be speculated that the translation-rotation coupling effect can weaken the dispersion behaviors when the strain softening occurs. The degree of attenuation for S1 wave is much smaller than that for P1 wave, and the attenuation for S2 wave is almost zero. However, at the softening stage, the degree of attenuation for S1 wave increase sharply. For the R wave mode, there is a same cutoff frequency for different stress-strain stages, and the cutoff frequency is the frequency with zero wave number.And the evolution law of dispersion behavior for R wave is similar to that for P1 wave at different stress-strain stages, but the plasticity has smaller effect on the degree of dispersion behavior for R wave than that for P1 wave. And no attenuation for R wave is predicted based on Eq. (19).
We can also compare dispersion behaviors for the unsaturated granular media predicted under the Cosserat framework to those under the classical framework. Figure 3 shows the disper-sion and attenuation curves of Cosserat vs. classical wave modes, considering plastic stage 1 for an example. For both dispersion and attenuation curves, the Cosserat P1 and P2 waves are identical with the classical ones. The Cosserat S1 wave is close to the classical S wave, and the Cosserat S2 wave is close to the Cosserat R wave. Therefore, it can be concluded that the Cosserat P1 and P2 waves correspond to the longitudinal wave mode, the Cosserat S1 wave corresponds to the transverse wave mode, and the Cosserat S2 wave corresponds to the coupled transverse and rotational transverse wave mode. And the Cosserat R wave corresponds to the rotational longitudinal wave mode.

Table 1 Values of parameters for different stages
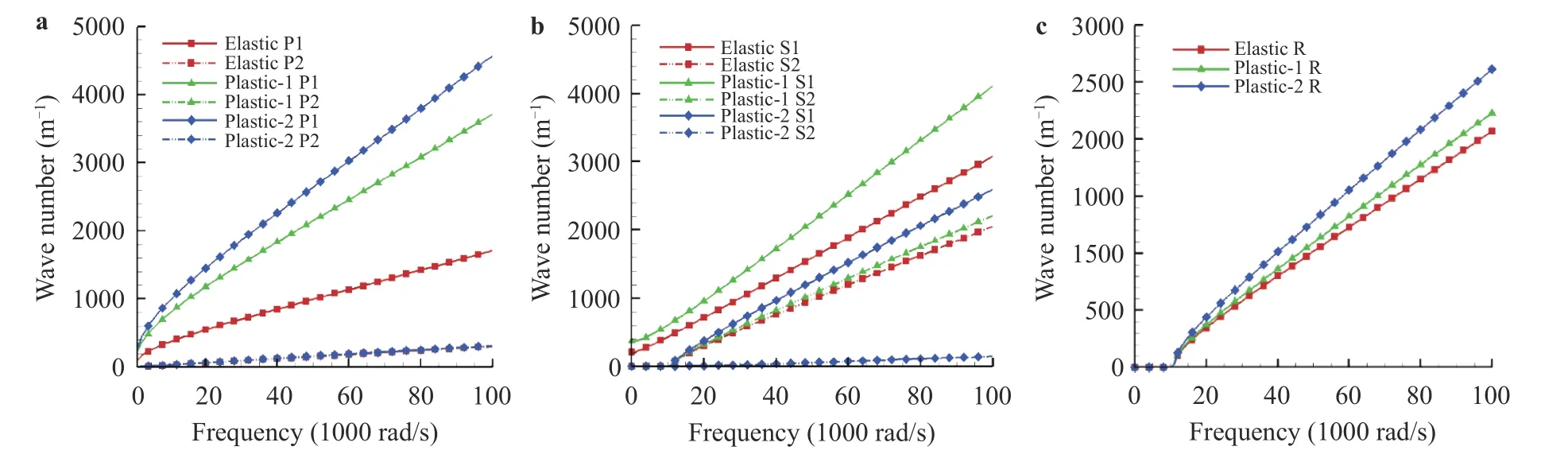
Fig. 1. Dispersion curves ω-kr for a P wave, b S wave and c R wave at different stress-strain stages: elastic stage, plastic stage 1 and plastic stage 2
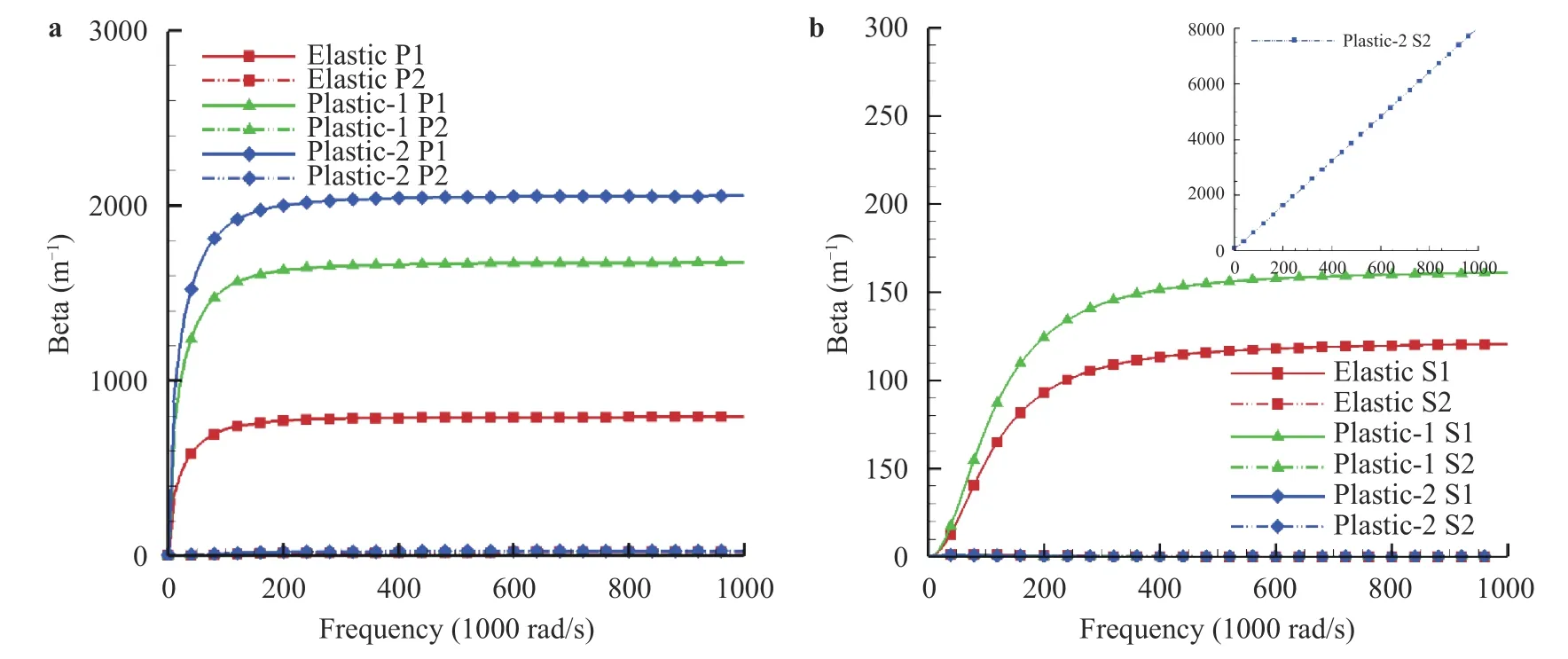
Fig. 2. Attenuation curves ω-β for a P wave and b S wave at different stress-strain states: elastic stage, plastic stage 1 and plastic stage 2
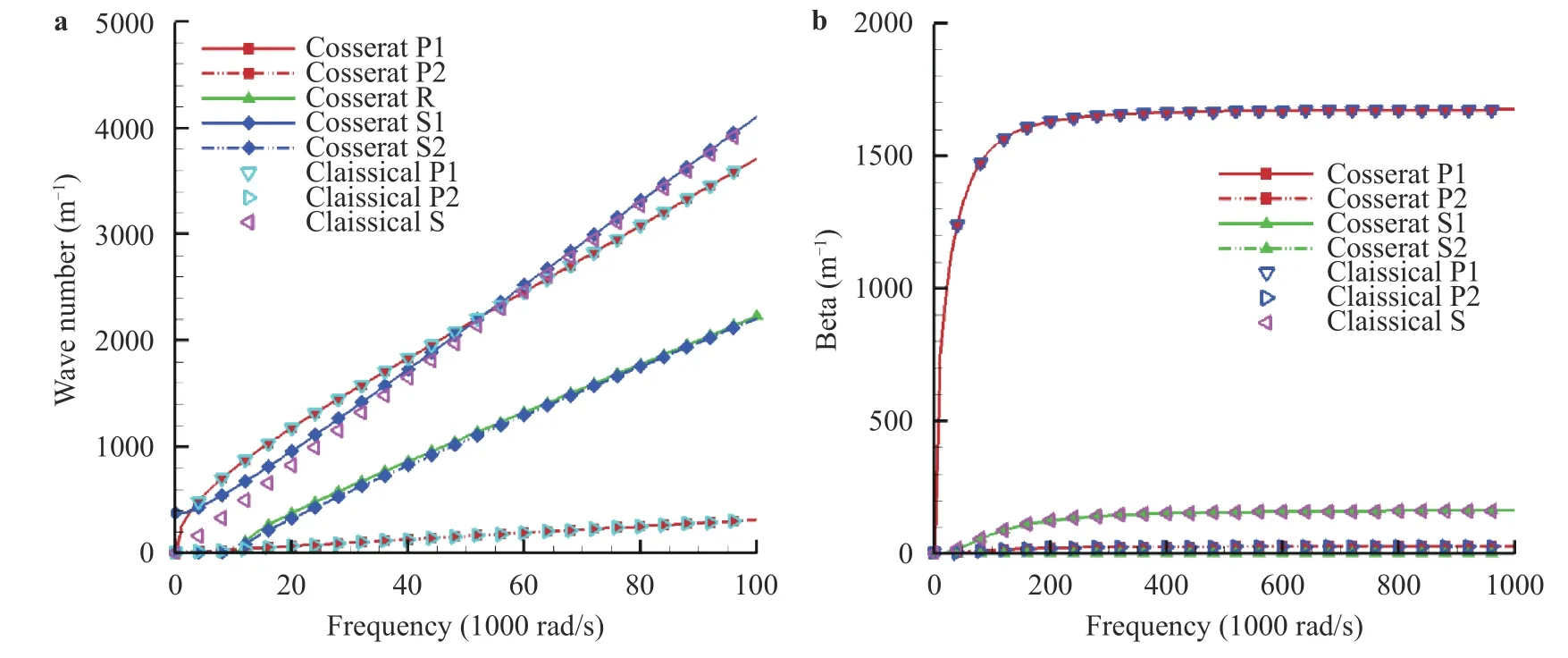
Fig. 3. a Dispersion curves ω-kr and b attenuation curves ω-β of Cosserat vs. classical wave modes at plastic stage 1
In summary, the wave equations and dispersion equations are derived for the elastoplastic unsaturated granular media based on the Cosserat theory. Due to symmetry, five wave modes are predicted and reduced from seven waves for the propagation of a plane wave, including two longitudinal waves (P1, P2 waves), two coupled transverse - rotational transverse wave (S1,S2 waves) and one rotational longitudinal wave (R wave). The dispersion behaviors of these wave modes are obtained. Dispersion behaviors for Cosserat P1, P2 waves of unsaturated granular media are identical with those for classical P1, P2 waves. R and S2 waves are predicted by the Cosserat theory but absent in classical theory. Different stress-strain stages have effect on the dispersion behaviors. With the increase of the degree of plasticity, dispersion behaviors get more obvious for P1 and R waves and have no change for P2 wave, and the softening stage makes an inverted change for the state of dispersion behaviors for S1,S2 waves. This is mainly because the translation-rotation coupling effect can weaken the dispersion behaviors when the strain softening occurs.
Acknowledgements
The authors are pleased to acknowledge the support of this work by the National Natural Science Foundation of China(Grants 11772237 and 11472196) and to acknowledge the open funds of the State Key Laboratory of Structural Analysis for Industrial Equipment (Dalian University of Technology) (Grant GZ19110).
杂志排行
Theoretical & Applied Mechanics Letters的其它文章
- Editorial: Computational granular mechanics
- Construction of irregular particles with superquadric equation in DEM
- A block particle coupled model and its application to landslides
- Modified virtual internal bond model based on deformable Voronoi particles
- Modeling of deformation processes in rock massif in the vicinity of underground goafs considering the formation of discontinuity zones
- Application of multi-dimensional wavelet transform to fluid mechanics
