Modified virtual internal bond model based on deformable Voronoi particles
2020-06-06OlegKonovalovShunyingJiMichaelZhuravkov
Oleg Konovalov, Shunying Ji, Michael Zhuravkov*
a Research Laboratory of Information Technologies and Computer Graphics, Belarusian State University, Minsk 220030, Belarus
b DUT-BSU Joint Institute, Dalian University of Technology, Dalian 116023, China
c State Key Laboratory of Structural Analysis for Industrial Equipment, Dalian University of Technology, Dalian 116023, China
d Department of Theoretical and Applied Mechanics, Belarusian State University, Minsk 220030, Belarus
Keywords:Discrete element method Real multi-dimensional internal bond Voronoi tessellation Micromechanical poisson ratio Barycentric coordinates Auxetic effects
ABSTRACT In last time, the series of virtual internal bond model was proposed for solving rock mechanics problems. In these models, the rock continuum is considered as a structure of discrete particles connected by normal and shear springs (bonds). It is well announced that the normal springs structure corresponds to a linear elastic solid with a fixed Poisson ratio, namely, 0.25 for threedimensional cases. So the shear springs used to represent the diversity of the Poisson ratio.However, the shearing force calculation is not rotationally invariant and it produce difficulties in application of these models for rock mechanics problems with sufficient displacements. In this letter, we proposed the approach to support the diversity of the Poisson ratio that based on usage of deformable Voronoi cells as set of particles. The edges of dual Delaunay tetrahedralization are considered as structure of normal springs (bonds). The movements of particle's centers lead to deformation of tetrahedrals and as result to deformation of Voronoi cells. For each bond, there are the corresponded dual face of some Voronoi cell. We can consider the normal bond as some beam and in this case, the appropriate face of Voronoi cell will be a cross section of this beam. If during deformation the Voronoi face was expand, then, according Poisson effect, the length of bond should be decrees. The above mechanism was numerically investigated and we shown that it is acceptable for simulation of elastic behavior in 0.1-0.3 interval of Poisson ratio. Unexpected surprise is that proposed approach give possibility to simulate auxetic materials with negative Poisson's ratio in interval from -0.5 to -0.1.
A number of authors used the lattice spring (LS) approach for modeling the crack propagation in elastic rock environment [1].In bound of this approach, the virtual internal bonds (VIB) model has been developed, where a continuous medium are determined as discretized model of microstructural relationships. The improved model of virtual multidimensional internal bonds(VMIB) was proposed by Zhang and Ge [2]. In VMIB model bonds are broken down into components: normal and tangential forces are considered separately. At the current time, Zhao et al. [3] proposed the real multidimensional internal bonds(RMIB) model, where the bonds are determined by the contact of the particles in some packaging of the simulated medium. In our research we will using packaging structure based on the ordinary Voronoy discretization. In this case, bonds are the network of edges in dual Delaunay tetrahedralization of modeled domain.
In RMIB model, each bond contains two springs: a normal spring and a shear spring where, knand ksare respectively the normal and shear stiffness of bond. The deformation vector uijof the bond (Fig. 1), that connected particles i and j, decomposes into a normaland a shearcomponents. The normal and shear forces acting on the particle are:. If the bond's deformation reach the critical value (i.e. uij> δ0), the bond goes to the broken state. In this state, the normal spring still elastically works on compression, but does not exert a tensile strength. The forces, that arise when the shear spring is deformed, should be are decreased and works as friction forces.In RMIB theory, the relationship between properties of discretized 3D model kn, ksand properties of continuous 3D model E, ν is given [2]:
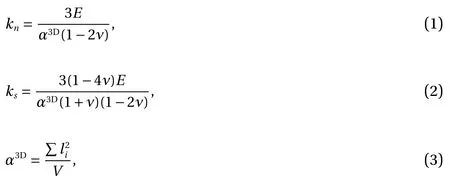
where E, ν, V, and l are respectively the Young's modulus,Poisson ratio, volume of modeled media and average bond length.
For the shear spring, the relative shear displacement between two particles can be obtained simply aslike in some conventional lattice spring models. However, the shearing force calculated in this way is not rotationally invariant. To overcome the problem, Zhao et al. [3] has proposed a local strain based method.
In this method, the local strain of one particle is evaluated by a least square scheme which only uses the displacement of itself and other particles which have intact bonds with the particle.Based on above neighbor information the inverse of global transformation's matrix can be calculated. Unfortunately, in a practical simulation, the inverse of transformation's matrix may not exist in some conditions [3].
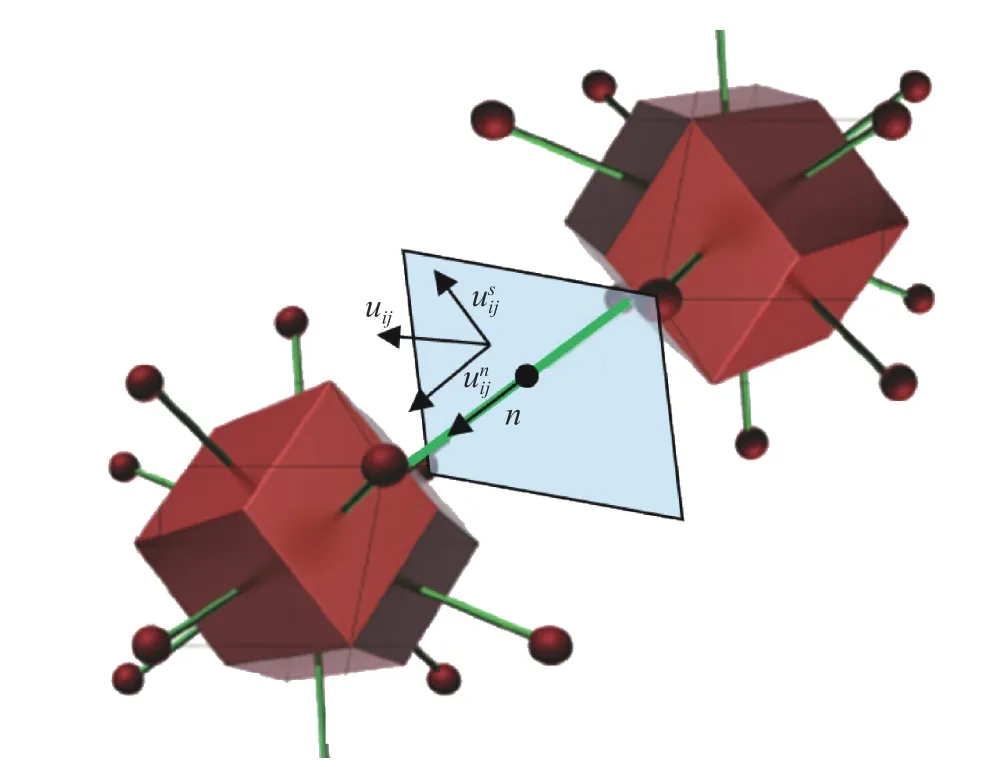
Fig. 1. Shear and normal displacement in RMIB
Take into accounting that the shear springs used to represent the diversity of the Poisson ratio, our proposal is to remove shear springs from calculation scheme. The diversity of the Poisson ratio will be implemented based on another mechanism -local deformation of particles.
Voronoi tessellation has many applications in natural science, engineering, geometry, etc. Polycrystalline microstructures are generally represented using Voronoi tessellations in material science. In geotechnical engineering, Voronoi tessellation is commonly used to generate block geometry.
Each Voronoi vertex is the circumcenter (CC) of some tetrahedron from the dual Delaunay 3D tessellations. In common case, the CC do not belong to pattern tetrahedron, but it is linear complexity problem to find tetrahedron contained CC.
Once above tetrahedron was found, the problem of finding the barycentric coordinates of CC are reducing to inverting a 3×3 matrix:

where (xi, yi, zi) is the Cartesian coordinates of the tetrahedron's vertices.
3D barycentric CC coordinates may be used to interpolate a new coordinates of Voronoi vertices after particles movement on next RMIB iteration step (exclude shearing force calculat). As result, we receive some transformation of Voronoi cell, which will be considered by us as local deformation of RMIB particle.
It should be noted, that after this deformation, the Voronoi cell will not remain convex. The lumps of Voronoi face (Fig. 2)that belong to different tetrahedrons, will not remain belong to one 3D plane.
The movements of particles centers lead to deformation of bond's tetrahedral network and as result to deformation of Voronoi cells. For each bond, there are the corresponded dual Voronoi face. We can consider the normal bond as some beam and in this case, the appropriate face of Voronoi cell will be a cross section of this beam. If during deformation the Voronoi face was constrict, then, according Poisson effect, the length of bond should be increase (Fig. 3). This can be approximated by following simple equation:
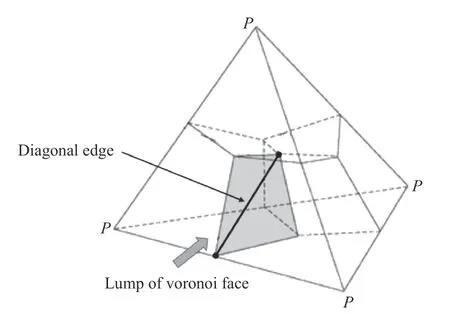
Fig. 2. Lump of Voronoi face and it's diagonal edge

where ΔL is enlargement of bond's length, rinis radius of circumscribed circle of initial Voronoi face, rdfis radius of circumscribed circle of deformed Voronoi face, νmicrois micromechanical Poisson ratio.
It should be pointed that νmicrois not equal to macro Poisson ratio. It is follow from well-known fact that the normal springs random structure corresponds to a linear elastic solid with a fixed Poisson ratio, namely, 0.25 for three-dimensional cases.This reasoning leads us to conclusion that for macro Poisson ratio 0.25 the νmicroshould be equal to zero. As will be shown below, it is not strictly sou. It should be noted that the range of values of the micromechanical Poisson ratio is much larger than for the macro Poisson ratio, so its value can be more than 0.5. We have find that proposed numerical scheme stable works in range from -0.8 to 0.8. In any case, the relationship between macro and micro Poisson coefficients should be investigated experimentally.
The real transformation of Voronoi face is match more complex than described by Siméon Poisson phenomenon (constriction and expansion). To estimate (rin-rdf)/rinin more complex cases we will use simple heuristic:
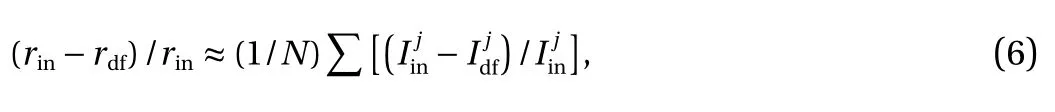
where N is number of vertices in Voronoi face,is length of j-m diagonal edge in initial Voronoi face,is length of deformed diagonal edge.
If we try to describe the proposed model formally, we can pointed following main features:
· this is real onedimensional internal bonds model;
· we use packaging structure based on the ordinary Voronoi discretization;
· lengths of bonds are modified on each iteration step according local deformation of Voronoi cells.
We named the above model as deformable Voronoi (DV)model. The first numerical experiments with DV show that this very simple model have very big simulation potential.
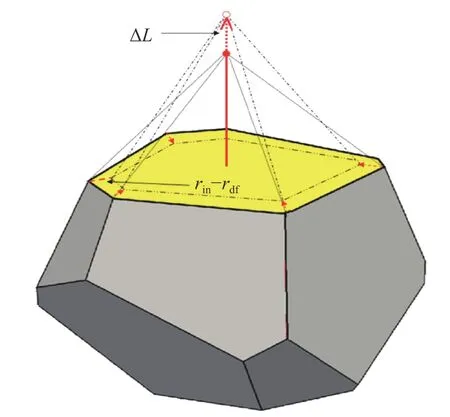
Fig. 3. Micromechanical Poisson effect
The above approach is acceptable for simulation of elastic behavior in 0.1-0.3 interval of Poisson ratio. Unexpected surprise is that DV model give possibility to simulate auxetic materials with negative Poisson's ratio (Fig. 4) in interval from -0.5 to -0.1.
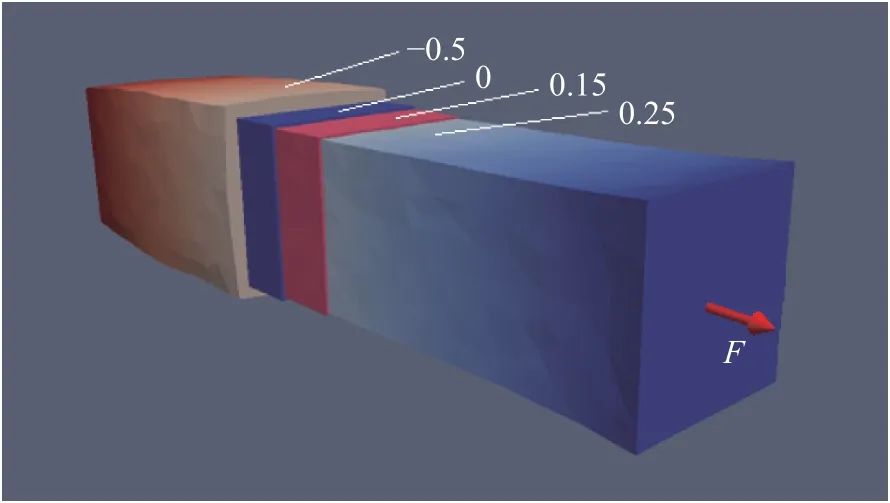
Fig. 4. DV-simulation of Poisson effect
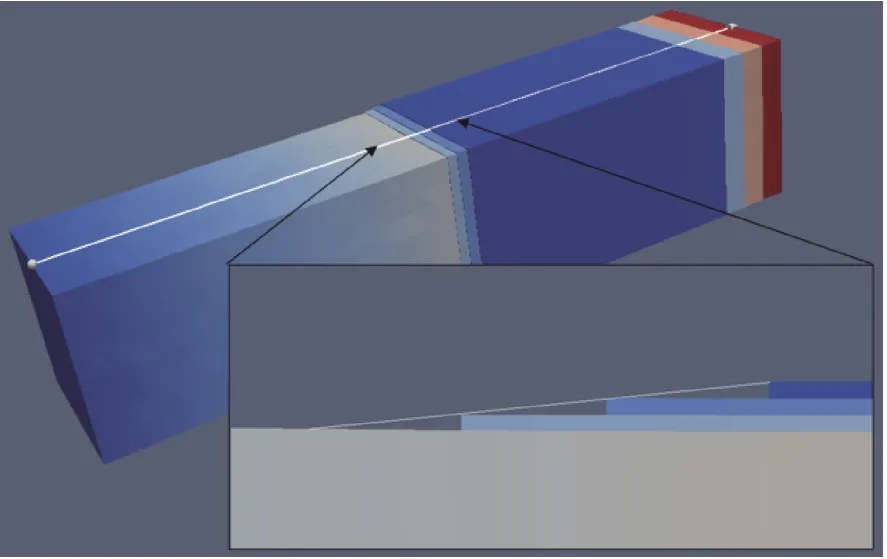
Fig. 5. Linear relationship between the square beam length enlargement and there cross section constriction

Table 1 Dynamic parameters of numerical series

Fig. 6. Reconstructed Poisson ratios for series 1 and 2
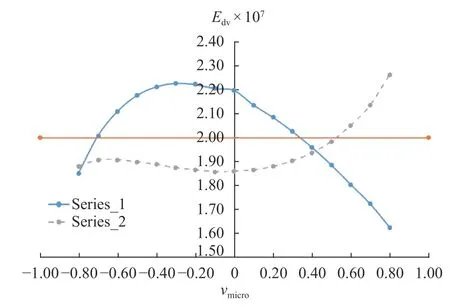
Fig. 7. Reconstructed Young's modulus for series 1 and 2
Figure 5 demonstrates linear relationship between square beam length enlargement and there cross section constriction during DV simulation.
We had incorporated in our model the micromechanical Poisson effect to reach the diversity of the macro Poisson ratio.To investigate the relationship between macro and micro Poisson ratios the series of numerical experiments was performed.As it present on Fig. 4, the left end of the beam is fixed and the right end is subjected to a normal force. The scope of varied parameters are presented in Table 1 and the static parameters are: E = 20 MPa, ρ = 2500 kg/m3, ν=0.25.
For each numerical experiment two elastic parameter was reconstructed: model's Young's modulus Edvand Poisson ratio νdv.The results of experiments are presented in Figs. 6 and 7. To avoid the misunderstanding it should be pointed that static parameters E and ν are used only for calculation of the bond's normal stiffness knaccording Eq. (1).
The analysis of experiments gives us many interesting things.The Poisson ratio reconstruction shows that it exist practical applicable interval (from 0.1 to 0.3) where the relationship between macro and micro Poisson ratios is near linear. Another interesting fact is that neighborhood of νmicro= -0.5 correspond to volume incompressible cases. When νmicro< -0.5 we received auxetic effect. What is surprised, that according the numerical experiments the normal springs random structure corresponds to a linear elastic solid with a Poisson ratio 0.2 instead of expected 0.25. This fact not understandable and need more depth investigation.

Fig. 8. Size of simulated beam and boundary conditions
The Young's modulus reconstructed for series 1 is near to parabolic low with center νmicro= -0.2. The maximum divergence from expected E = 20 MPa is around 20%. To overcome above we incorporate in kncalculation the dependence from νmicro:
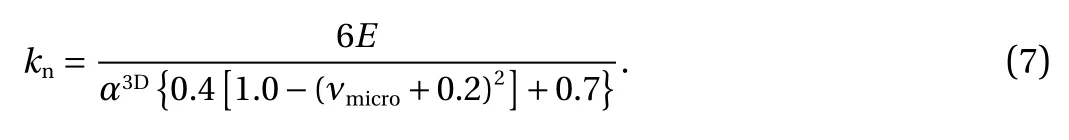
The Young's modulus reconstruction for series 2 was performed for kncalculated according Eq. (4). In this case, the maximum divergence from expected E is around 10%. The above give us expectation that during next investigation we will receive more convenient way to calculate the bond's normal stiffness kn.
For verification of elastic behavior RMIB method, Zhao et al.[3] performed the series of numerical tests . The RMIB simulation results of the “beam subjected to bending” problem were compared with finite element method (FEM) solutions. The estimated error of displacement in vertical direction was in around 1.5%.
We used for verification of DV method the same approach.Instead of Zhao et al. [3] we used bending beam problem II.Figure 8 gives the geometry information and boundary conditions. The left and right ends of the beam are fixed and the beam is subjected to a gravity force. The static simulation parameters are: E = 20 MPa, ρ = 2500 kg/m3.
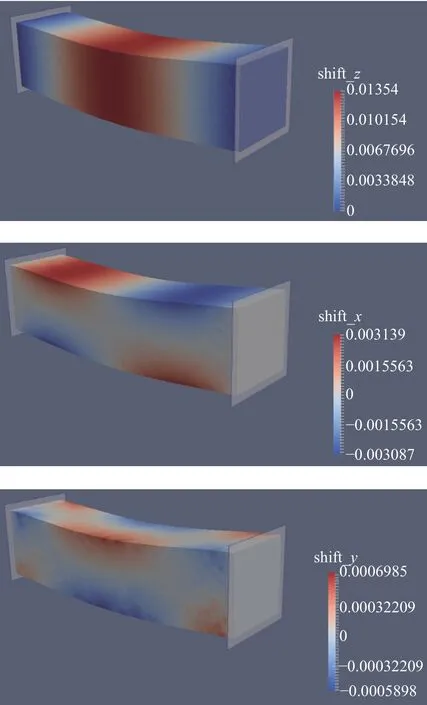
Fig. 9. DV-simulation of bending beam problem

Fig. 10. FEM and DV vertical and horizontal displacements along the middle line
The beam will undergo a complex stress condition, i.e.tensile, compressive and shear stress would appear. Figure 9 shows the DV-simulation results. It was found that the normal spring's model could reproduce the same displacement distribution as the FEM model. We performed the two numerical experiments for Poisson ratios 0.15 and 0.2. Quantitative comparison is given in Fig. 10, where the vertical and horizontal displacements along the middle line (Fig. 3) of the beam predicted by FEM and DV are shown.
For the vertical and horizontal displacements along the middle line, the maximum errors of the DV model for two mentioned experiments are around 1.5% and 2.5% respectively. This means the DV model can be regarded as a valid representation of isotropic elastic material for geotechnical applications.
We considering the presented results as preliminary, but DV method have big potential from our point of view. The removing the shear springs make this method more robust and convergence than RMIB model.
In current DV implementation, we are using the failure behavior of RMIB model. However, approximation of deformation fields based on deformable Voronoi cells give the possibility to incorporate more complex model of failure behavior based on the lumps of Voronoi face.
Our future works include also implementing the viscoelasticity behavior in DV-simulation of rock materials.
杂志排行
Theoretical & Applied Mechanics Letters的其它文章
- Editorial: Computational granular mechanics
- Construction of irregular particles with superquadric equation in DEM
- Prediction on dispersion in elastoplastic unsaturated granular media
- A block particle coupled model and its application to landslides
- Modeling of deformation processes in rock massif in the vicinity of underground goafs considering the formation of discontinuity zones
- Application of multi-dimensional wavelet transform to fluid mechanics
