Construction of irregular particles with superquadric equation in DEM

Siqing Wng, Dzinis Mrmysh, Shunying Ji,c,*

a State Key Laboratory of Structural Analysis for Industrial Equipment, Dalian University of Technology, Dalian 116023, China

b Department of Theoretical and Applied Mechanics, Belarusian State University, Minsk 22073, Belarus

c DUT-BSU Joint Institute, Dalian University of Technology, Dalian 116023, China

keywords:Discrete element model Multi-superquadric elements Poly-superquadric elements Irregular particles Granular bed

ABSTRACT Non-spherical particles are widely present in industrial production, and significantly affect the macro and micro characteristics of granular materials. Although the superquadric equation can be used to construct non-spherical particles, its disadvantage is that the particle shape is geometrically symmetric and strictly convex. In this study, two composed approaches are used to describe geometrically asymmetric and concave particle shapes, including a multi-superquadric model and a poly-superquadric model. The multi-superquadric model is a combination of several superquadric elements, and can construct concave and geometrically asymmetric particle shapes.The poly-superquadric model is a combination of eight one-eighth superquadric elements, and can construct convex and geometrically asymmetric particle shapes. Both composed models are based on superquadric equations, and Newton's iterative method is used to calculate the contact force between the elements. Furthermore, superquadric elements, multi-superquadric elements,and poly-superquadric elements are applied for the formation of complex granular beds, and the influences of particle shape on the packing fraction can be successfully captured by the proposed models.

The discrete element method (DEM) is one of the effective tools to study the potential mechanical properties of granular materials [1-3]. In this approach, two-dimensional discs and three-dimensional spheres were initially applied to DEM simulations because of the simplicity of the calculation and the efficient operation [4, 5]. However, the particle shape significantly affects the dynamic characteristics of the granular systems [6, 7].Meanwhile, the conclusions obtained from spherical systems are difficult to apply directly to non-spherical systems [8]. To reasonably describe the irregular particle shapes, different construction methods have been developed, including multi-sphere method [9, 10], dilated polyhedron elements [11, 12], superquadric equations [13, 14], and spherical harmonic function representations [15, 16]. Among them, the superquadric equation is a common approach for mathematically describing non-spherical particles, and can construct 80% of the solid shapes in nature [17]. However, the particle shapes with different aspect ratios and surface sharpness constructed by the superquadric equations are geometrically symmetrical and strictly convex,which limits the further engineering application of the superquadric element.

In recent years, the composed element method has been well developed, and the basic element is not limited to spherical particles [18]. Arbitrarily shaped particles can be composed of several spheres of varying sizes [19, 20]. A true cylinder was a combination of a cylindrical surface and two circular planes, and a spherocylinder model is a combination of a cylindrical surface and two hemi-spheres [21, 22]. Moreover, cobblestone-shaped particles consist of eight one-eighth ellipsoidal elements [23, 24].However, little effort has been devoted to the detailed description of composed superquadric models.

In this letter, the multi-superquadric model and the poly-superquadric model are introduced in detail and used to describe concave and geometrically asymmetric particle shapes. DEM is applied to simulate the formation of complex granular beds.Therefore, the traditional superquadric equation can be expressed as [25]

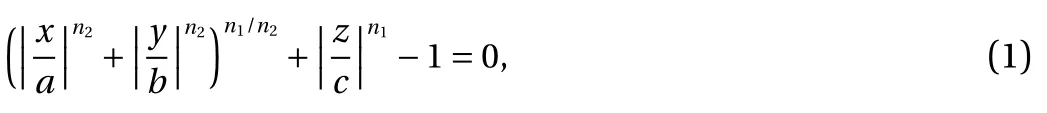
where a, b, and c are the semi-axis lengths of the superquadric elements along the major axis, respectively. n1and n2are the blockiness parameters and used to determine the particle shape.Figure 1 shows the basic particle model with different aspect ratios and surface sharpness obtained from the superquadric equation. A sphere or ellipsoid is obtained if n1= n2= 2, a cylinder-like particle is obtained if n1＞ n2= 2, a cube-like particle is obtained if n1= n2＞ 2. The particle shape theoretically becomes closer to real cylinders and cubes with sharp vertices and flat planes as the block parameters increase. However, the block parameters cannot be increased infinitely and need to be within a reasonable range, because it is limited by the search algorithm between superquadric elements.

Moreover, a multi-superquadric model is a combination of several superquadric elements [26], and the shape of the basic element is determined by Eq. (1). The basic elements can have different shapes, and there are different amounts of overlap between them. This model can be used to describe the concave,convex, and geometrically asymmetric particle shapes. Therefore, a multi-superquadric equation can be expressed as

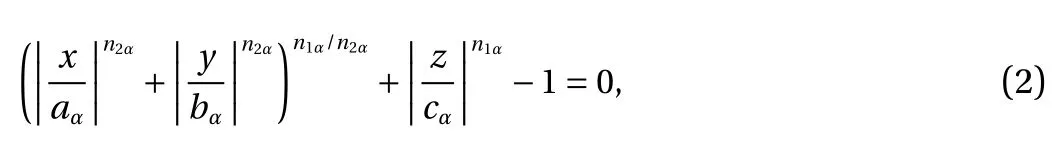
where aα, bα, cα, n1α, and n2αare shape parameters of the α-th superquadric equation. If a multi-superquadric model is composed of Nssuperquadric elements, a total of 5Nsshape parameters are required to represent the particle shape. Figure 2 shows the arbitrary shaped particles constructed by multisuperquadric models.

Another composed element method is a poly-superquadric model, which is a combination of eight one-eighth superquadric elements [27]. The shape of the basic element is controlled by Eq. (1), and this model can be used to construct convex and geometrically asymmetric shapes. A poly-superquadric equation can be expressed as

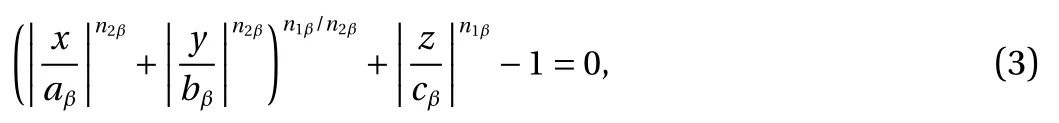
where aβ, bβ, cβ, n1β, and n2β(β = 1, 2, …, 8) are shape parameters of the β-th super-quadric equation. Therefore, 40 shape parameters are needed for describing a poly-superquadric model. Considering the smoothness and continuity of the particle surface, eight governing equations need to be satisfied

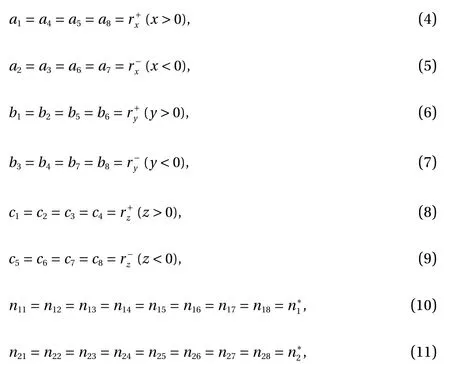
Considering the complexity of contact detection between multi-superquadric elements or between poly-superquadric elements, both composed models can be divided into several superquadric elements. Therefore, the contact detection between the composed elements can be transformed into the contact detection between the superquadric elements. It is worth noting that the contact forces between superquadric elements belonging to the same composed element are not calculated. Moreover,the midway point approach is used to calculate the contact force between adjacent elements i and j, and the corresponding nonlinear equations can be expressed as [28]

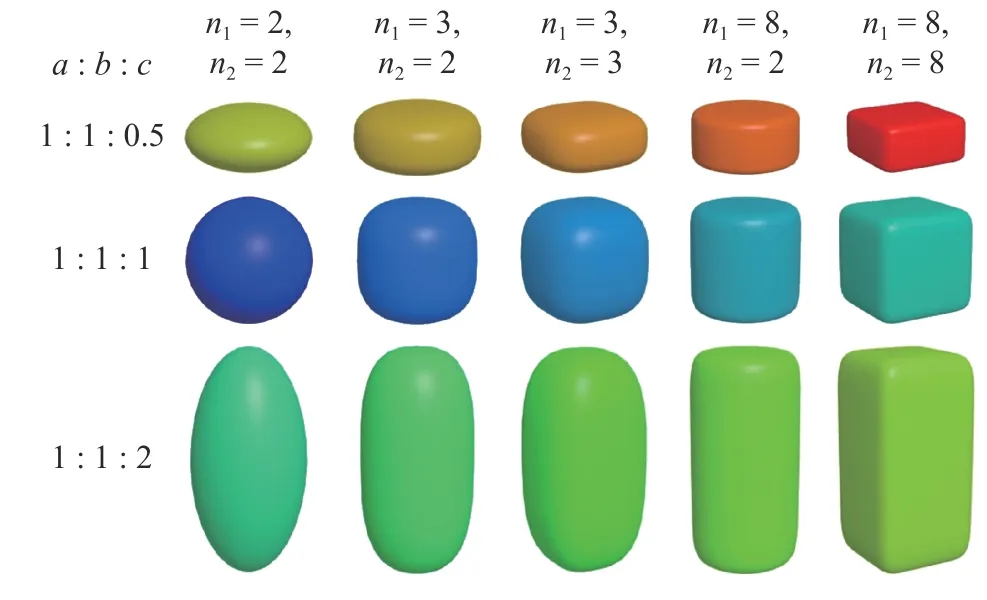
Fig. 1. Differently shaped particles constructed by superquadric equations.

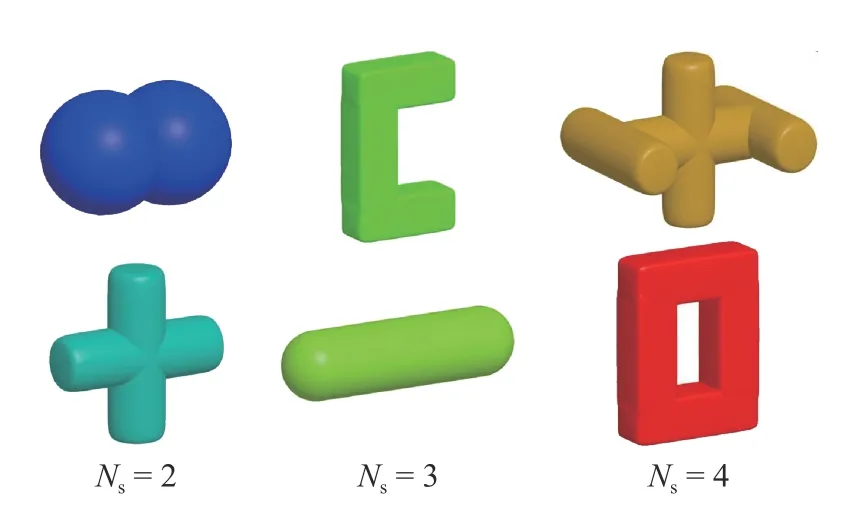
Fig. 2. Differently shaped particles constructed by multi-superquadric models.

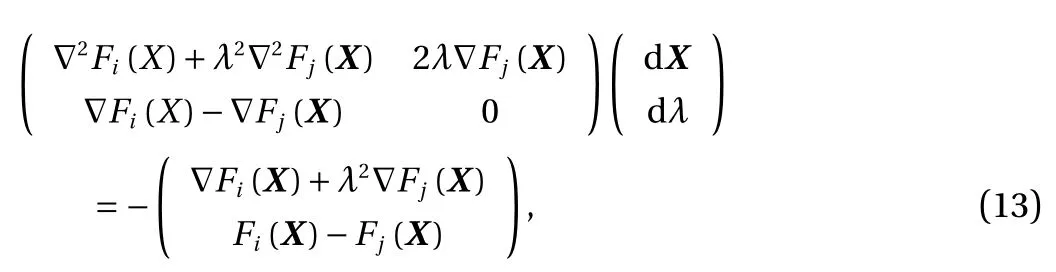
where X(k+1)=X(k)+dX(k)and λ(k+1)=λ(k)+dλ(k). If the midway point X0satisfies Fi(X0)＜0 and Fj(X0)＜0, the elements i and j are in contact. The normal direction can be obtained by n=∇Fi(X)/∇Fi(X), as shown in Fig. 4. Then, the surface points Xiand Xjsatisfy Xi= X0+ γn and Xj= X0+ τn, respectively. The unknown parameters γ and τ can be obtained by Newton iterative method [29]:andFinally, the normal overlap can be obtained by δn= Xi- Xj.

In DEM simulations, spherical non-linear contact models have been well established and successfully extended to nonspherical granular systems [30, 31]. The normal forces between the elements include elastic and damping forces, which can be expressed as

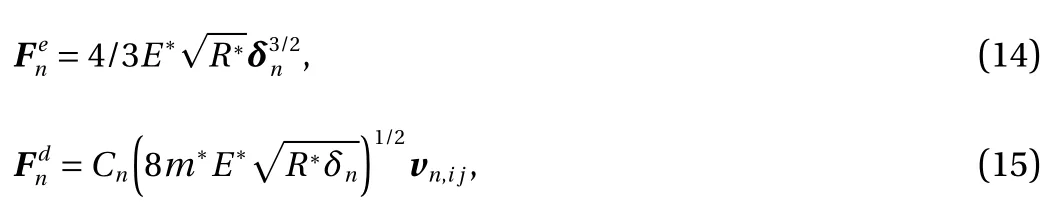
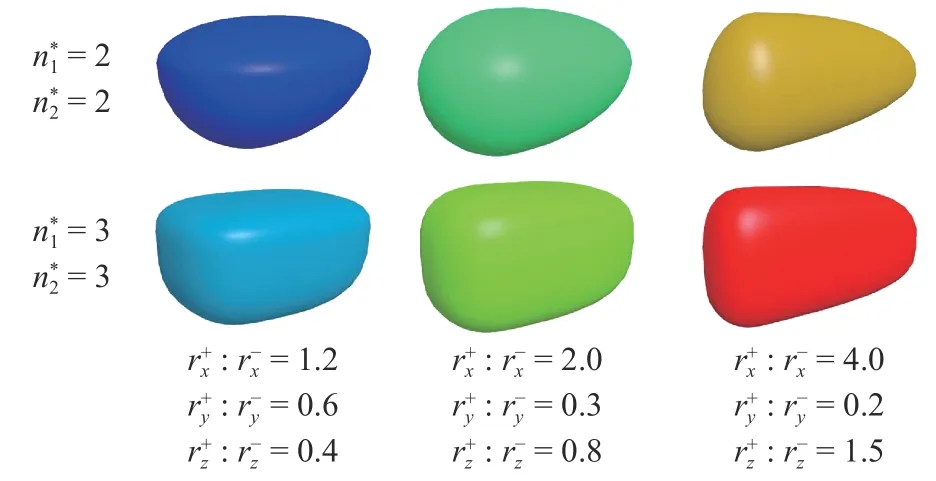
Fig. 3. Differently shaped particles constructed by poly-superquadric models.

The tangential contact force ( Ft) includes the elastic forceand the damping force, which are expressed as:

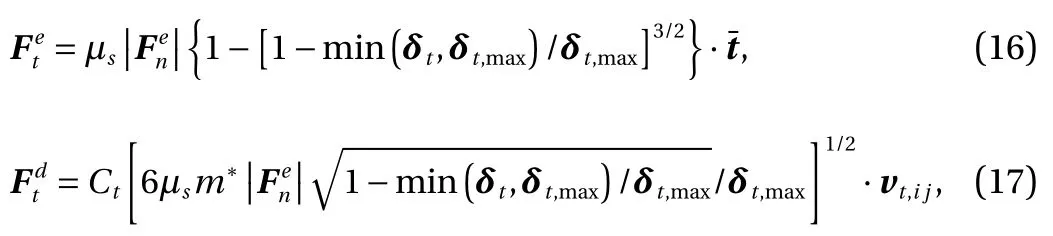
where μsandare the sliding friction coefficient and the tangential unit vector, respectively. δtis the tangential relative displacement, which is obtained by δt= δt+ vt,ij·dt. vt,ijis the tangential relative speed. δt,maxis the maximum tangential displacement, which is determined by δt,max=μs(2－υ)/[2(1－υ)·δn].

The rolling friction coefficient ( Mr) is used to hinder the relative rotation between the elements, which is expressed as

where μris the rolling friction coefficient.is the relative rotating speed, which is obtained by

To examine the applicability of the multi-superquadric model and poly-superquadric model, the formation of the nonspherical granular bed was simulated by DEM. Differently shaped particles have the same mass, and the diameter of a volume equivalent sphere is 5 mm. The total number of particles is 1500. The cubic container has a length and width of 60 mm and a height of 60 mm. The main DEM simulation parameters are listed in Table 1. Figure 5 shows the differently shaped particles constructed by a superquadric element, a poly-superquadric element, and a multi-superquadric element. They have random positions and orientations at the initial moment, and form a non-spherical granular bed under gravity, as shown in Fig. 6. It can be found that the particle shape significantly affects the packing characteristics of the particulate material. Concave particles have higher porosity and lower packing density compared to convex particles.

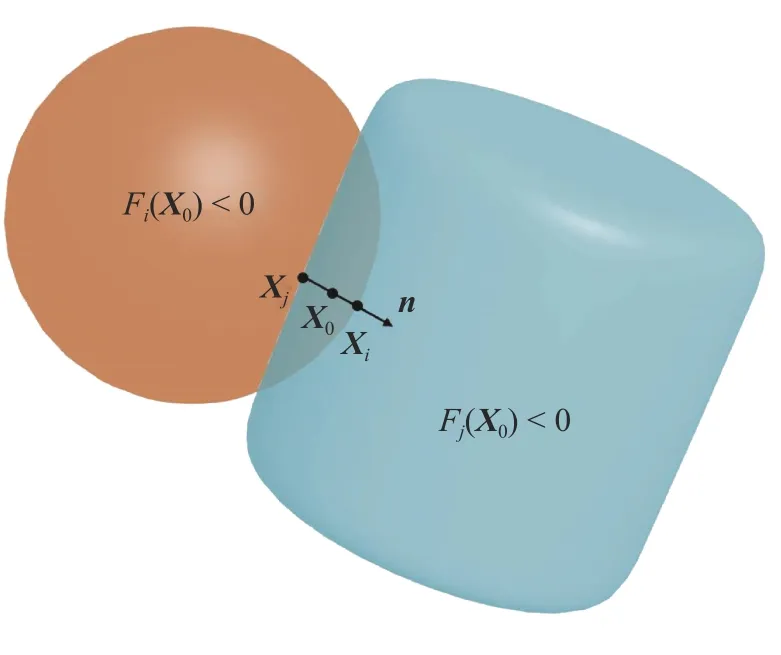
Fig. 4. Contact detection between superquadric elements.

Table 1 Major computational parameters of DEM simulations.

Fig. 5. Particles constructed by different models: a superquadric elements, b poly-superquadric elements, and c multi-superquadric elements.

Figure 7 shows the stable granular beds composed of differently shaped particles, and Fig. 8 shows the relationship between the particle shape and the packing fraction. Convex particles have a higher packing fraction than concave particles.This is because the interlocking between the concave particles causes local arching structure and more voids. As a result, the concave particles have a larger porosity and a lower packing density. Moreover, the geometric asymmetry of the particles facilitates the relative sliding between the elements and allows the particles to quickly fill the voids. As a result, geometrically asymmetric particles composed of poly-superquadric elements have a higher packing density than symmetric particles composed of superquadric elements.

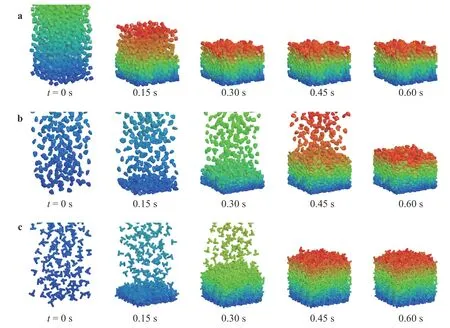
Fig. 6. Packing processes of granular beds composed of different models: a superquadric elements, b poly-superquadric elements, and c multisuperquadric elements.

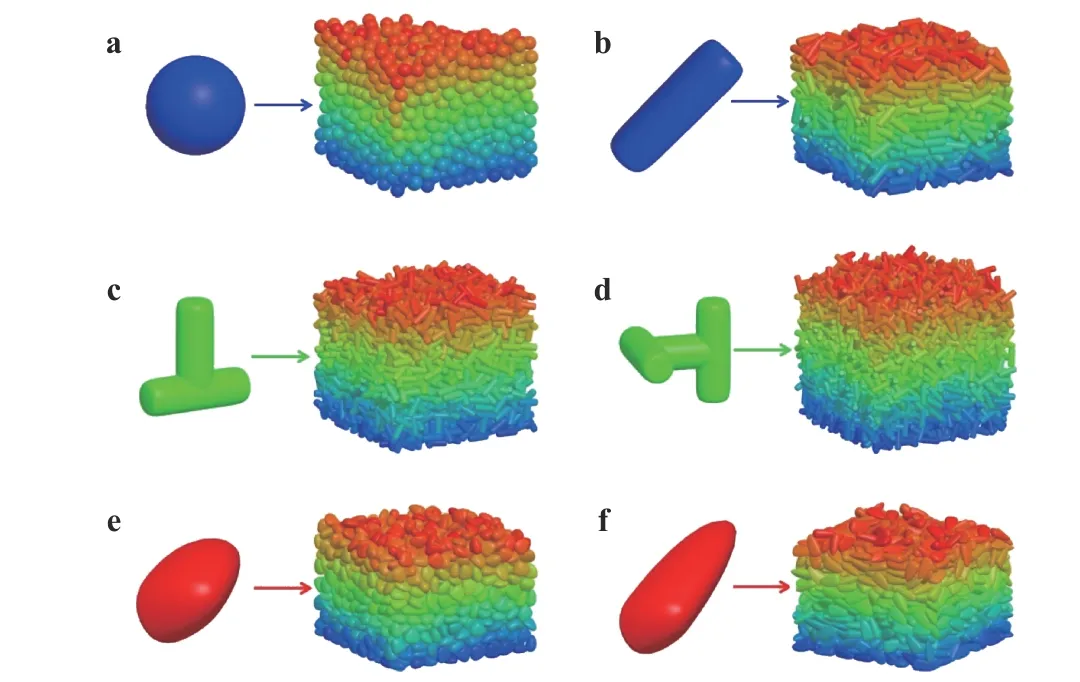
Fig. 7. Stable granular beds composed of different shaped particles: a, b superquadric elements, c, d multi-superquadric elements, and e, f poly-superquadric elements.

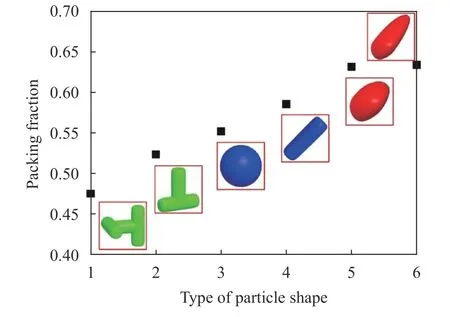
Fig. 8. Relationship between the particle shape and the packing fraction.

In this paper, we introduce a multi-superquadric model and a poly-superquadric model based on the superquadric Eq. (1),and the DEM is used to simulate the formation of the non-spherical granular beds. Multi-superquadric element is a combination of several superquadric elements, which can be used to construct concave, convex and geometrically asymmetric particles.Poly-superquadric element is a combination of eight one-eighth superquadric elements, which can be used to construct convex and geometrically asymmetric particles. For both composed models, Newton's iterative algorithm is used to calculate the overlap between elements, and the nonlinear contact model of spherical particles is used to calculate the contact force. Furthermore, the effect of particle shape on the packing fraction is investigated. The results show that the concave particles have a lower packing density than the convex particles. It is mainly because the interlocking between the elements causes locally arched structures and larger voids. In addition, geometric asymmetry makes it easier for elements to slide and reduce voids in the granular system. As a result, geometrically asymmetric elements constructed by poly-superquadric models have a higher packing density than geometrically symmetric elements constructed by superquadric models.

Acknowledgement

This study was financially supported by the National Key Research and Development Program of China (Grants 2018YFA0605902, 2016YFC1401505, and 2016YFC1402706), the National Natural Science Foundation of China (Grants 11872136 and 11772085) and the Fundamental Research Funds for the Central Universities (Grants DUT19GJ206 and DUT19ZD207).