Particle trajectories under interactions between solitary waves and a linear shear current

Xin Guan*

a Key Laboratory for Mechanics in Fluid Solid Coupling Systems, Institute of Mechanics, Chinese Academy of Sciences, Beijing 100190,China

b School of Engineering Sciences, University of Chinese Academy of Sciences, Beijing 100049, China

Keywords:Particle trajectories Linear shear current Solitary waves Direct numerical simulation

ABSTRACT This paper is concerned with particle trajectories beneath solitary waves when a linear shear current exists. The fluid is assumed to be incompressible and inviscid, lying on a flat bed. Classical asymptotic expansion is used to obtain a Korteweg-de Vries (KdV) equation, then a forth-order Runge-Kutta method is applied to get the approximate particle trajectories. On the other hand, our particular attention is paid to the direct numerical simulation (DNS) to the original Euler equations. A conformal map is used to solve the nonlinear boundary value problem. Highaccuracy numerical solutions are then obtained through the fast Fourier transform (FFT) and compared with the asymptotic solutions, which shows a good agreement when wave amplitude is small. Further, it also yields that there are different types of particle trajectories. Most surprisingly,periodic motion of particles could exist under solitary waves, which is due to the wave-current interaction.

Interactions between nonlinear water waves and currents play an important role not only in the mathematical theory of water waves, but also in our real life such as coastal and ocean engineering [1, 2]. In many cases of such phenomenon, for example, the motion of offshore platform in the ocean, it is necessary to study particle trajectories for some practical requirements, and this also helps us to better understand the flow structure beneath nonlinear waves.

When there is no current, it is well known that particles experience a backward-forward motion for periodic waves, following loops with a mean Stokes drift in the direction of wave propagation [3, 4]. On the other hand, all particles move in the direction of wave propagation without backward motion at all for solitary waves. This is proved by Constantin and Escher [5]based on a rigorous mathematical argument. Approximate analytical results were obtained by Borluk and Kalisch [6] and Gagnon [7] using the Korteweg-de Vries (KdV) equation. In the case of waves on currents with a uniform or sheared profile,mathematical properties of travelling waves have been established, including symmetry [8, 9], existence [10] and analyticity of streamlines [11]. The corresponding flow structure for smallamplitude periodic waves were also studied by Constantin and Villari [12], Ehrnström & Villari [13], and Wahlén [14]. Except for the Eulerian formulation, Zaman and Baddour [15], Chen et al.[16] and Hsu [17] used a Lagrangian formulation to describe wave-current interactions and particle trajectories. Their works yield that the mean level of a particle orbit over its period is higher than in the Eulerian formulation. Such inconsistency of two apparently equivalent systems has already been indicated by Provenzale et al. [18] in the study of particle trajectories under solitary waves, and they believed this difference comes from a mixing of perturbation order when using asymptotic expansions.On the other hand, periodic waves and solitary waves on a linear shear current has been widely studied based on the direct numerical simulation (DNS) (see [19-24] for example). Da Silva Teles et al. [19] used a boundary integral formulation to show that there exist closed streamlines or so-called cat's eyes in the frame of reference following waves. A similar result with respect to solitary waves with a shear current was also obtained by Johnson [25] using the asymptotic method. Same results were found analytically by Choi [26] using his strong nonlinear model, and by Ribeiro et al. [22] using a conformal map method. Kharif and Abid [27] proposed a new model derived from the Euler equations for fully nonlinear waves in the presence of linear shear current. From this model they derived a generalised Whitham equation which simplifies to the KdV equation previously obtained in Ref. [26]. At the same time, Hur [28] also derived shallow water wave models with constant vorticity and studied their stability. Curtis et al. [29] used a higher-order nonlinear schrödinger equation to study the effects of background shear on the modulational instability and particle trajectories. Most refereces cited above focused on the calculation of solitary waves, however, particle trajectories for solitary waves on a linear shear current through the direct numerical simulation (DNS)has rarely been studied so far, and this is what we focus on in this paper.

Consider an incompressible and inviscid fluid layer with constant density on a flat bed. The depth of the layer is h when the fluid is at rest. Inside the fluid there is a linear shear current so a constant vorticity with strength － ω exists everywhere. We set the undisturbed free surface to the level z =0, and the linear shear current is written as U =ωz. We assume that a disturbance which has potential φ (t,x,z) occurs at some time and the free surface has an elevation η (t,x), then we have the following governing equations:

In the domain － h ＜z ＜η:

On the rigid bottom z =－h:

On the free surface z =η:

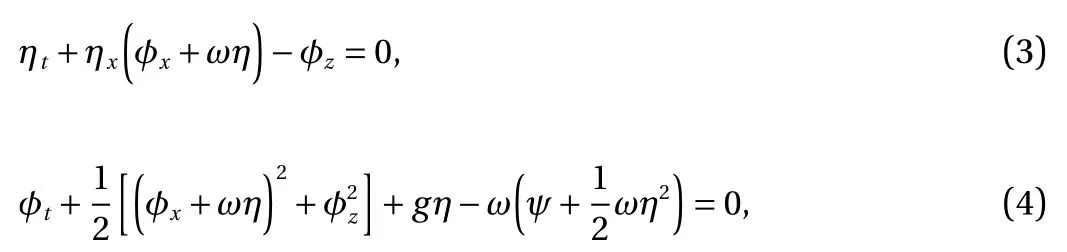
where ψ is the complex conjugate of φ , and g is the gravitational acceleration. Our purpose is to solve η and φ, then calculate the particle trajectories.

Under the long-wave and small-amplitude assumption, we can derive the classical KdV equation. Assume the typical horizontal length scale is λ and introduce the typical velocitythen the following Boussinesq scaling is chosen:

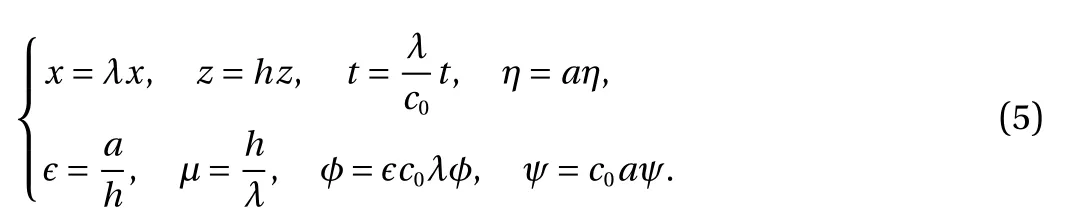
The governing equations now become

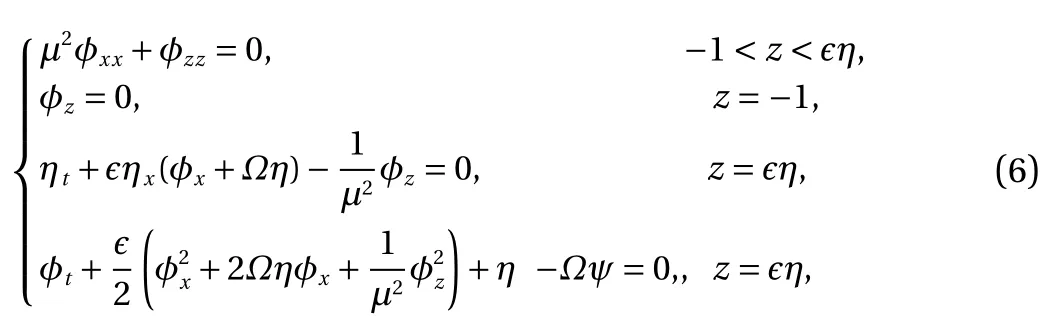
where A =φ(t,x,－1) represents the pontential function on the bottom. Substitute Eq. (7) into the two boundary conditions and we can obtain the following equation by neglecting the secondorder terms

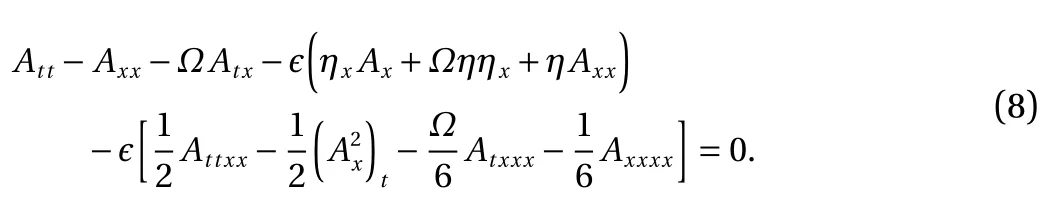
To obtain the KdV equation, the relation η=－At+ΩAx+O(ϵ)is used and Eq. (8) is rewritten by introducing new variables:

where c by the linear terms in Eq. (8) satisfies

Ultimately we have

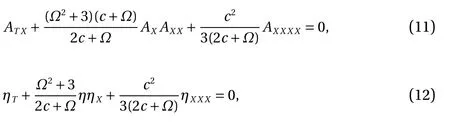
it is noted that Eq. (10) has been used to simplify the coefficients.Equation (12) is consistent with the equation obtained by Choi[26] after some variable transformation due to a different frame of reference. The travelling wave solutions are obtained immediately

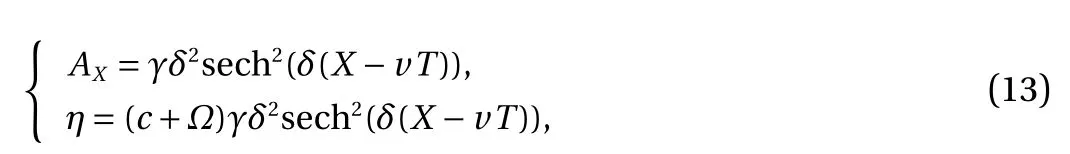
or equivalently

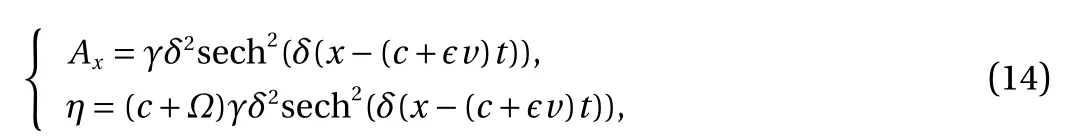
It is noted that the solitary waves are always of the elevation type, and for a fixed Ω there are two branches of solutions moving to right and left respectively.

To obtain particle trajectories, we need to solve the following nonlinear differential equations,

and the forth-order Runge-Kutta method is used for the time integration. Here, to get some insights into the flow structure, it is convenient to choose a frame of reference moving with the wave, so we can approximate the stream function by

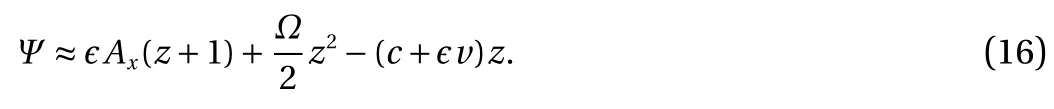
It is interesting to note there exist closed streamlines. To see this, take the derivative of Eq. (16) with respect to z yields

On the vertical line x =0, we have

Note when Ω and c have different sighs,=0 would has a root in the fluid domain, but this requires that ϵ is not too small sinceand u =0 due to the symmetry. So there exists a stagnation point and it is surrounded by a family of closed streamlines nearby.

To perform a DNS to the full Euler equations, a conformal map technique is used to map the physical domain onto a canonical strip, see also [22, 23]. The new variables ξ and ζ are introduced and the conformal map is defined as F(ξ,ζ)=x(ξ,ζ)+iz(ξ,ζ). The free surface and the bottom are mapped to ζ =0 and ζ =－1 respectively. For this purpose we need to solve the following boundary value problems

and

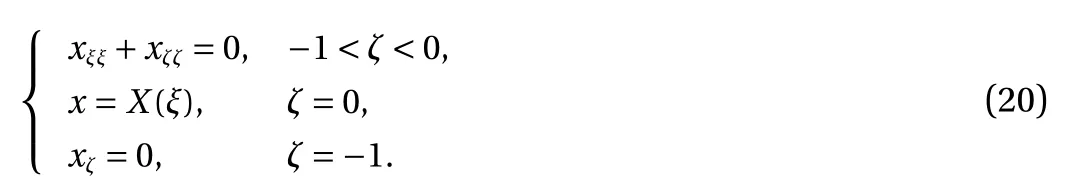
These equations can be solved analytically. We take Eq. (19)for example. If we introduce z′=z－ζ which satisfies the corresponding homogeneous equation, and take the Fourier transform with respect to ξ, then we obtain an ordinary differential equation

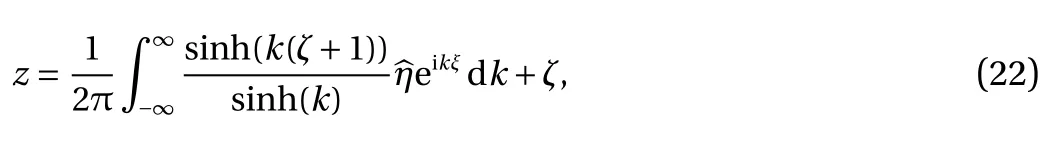
similarly the solutioin of Eq. (20) is

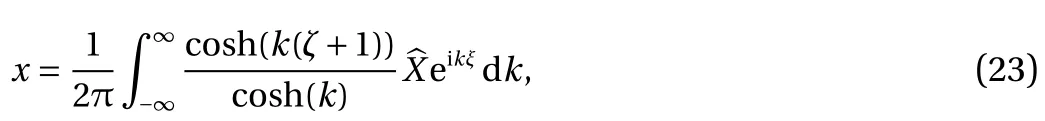
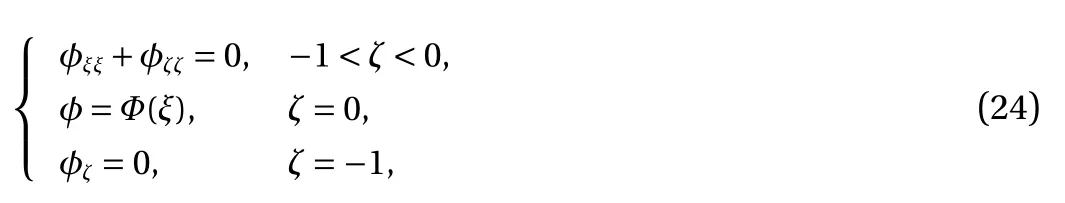
and

the solutions are given by

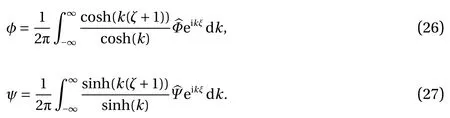
According to the Cauchy-Riemann equation xξ=zζand φξ=ψζ, we have the following identities on the free surface ζ=0

where δ (k) is the Dirac delta function. Since we are seeking travelling-wave solutions, it is convenient to choose a moving frame of reference so that waves become steady. Again we chooseas the typical speed and other quantities are nondimensionalised by

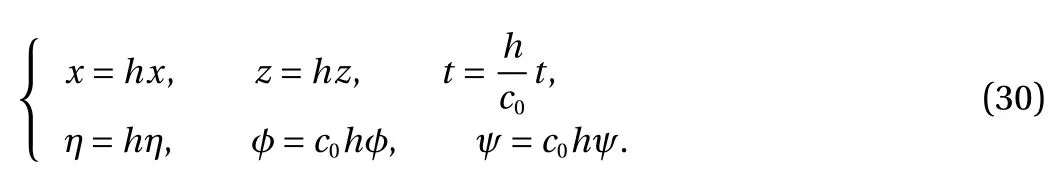
Then the kinematic boundary condition and the Bernoulli equation are

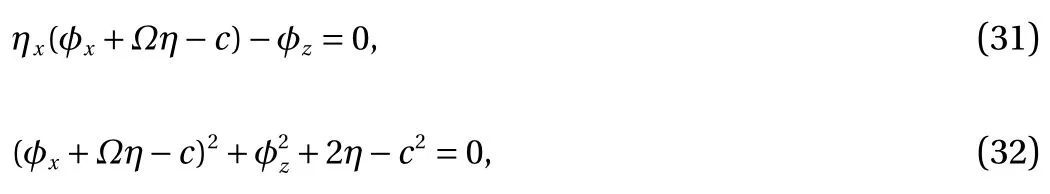
where Ω is defined as before. Using the new variables ξ and ζ,two boundary conditions can be recast to

To solve the nonlinear Eq. (34) numerically and obtain a travelling solitary wave solution, we take a long equally spaced grid points of ξ at ζ =0:

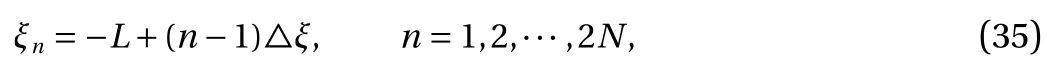
where △ξ=L/N , and N is a large number. With an even symmetry of η about ξ =0, we actually have N +1 unknowns ηi=η(ξi), i =1,2,···,N+1. Together with the wave speed c under a given wave height H, this gives rise to a set of N +1 equations for N+2 unknowns (η1,···,ηN+1,c). The system is closed by adding the restriction about the wave height,

Equations (34) and (36) are solved by Newton's method, with a small-amplitude solitary wave profile as initial guess. All the derivatives and integrals are calculated by their discrete Fourier representations using FFT. The Jacobian of the system for the Newton iteration is constructed by finite variations in the unknowns. The computation is stopped under the condition that the infinite norm of the system's deviation from zero is less than 10－10.

There are two branches of solutions for a fixed value of Ω,corresponding to right-going waves and left-going waves. When Ω is replaced by － Ω, the solutions are simply changed by reversing c to － c . So in our calculation, we always choose the branches with positive c .

When η and c are obtained, the whole velocity field can be calculated via Eqs. (22), (23), and (26)-(29). So the particle trajectories can be found by a time integral and we use the forth-order Runge-Kutta method.

To confirm the accuracy of DNS, we compare the values of wave speed c when different numbers of mesh points are considered in Table 1 firstly. For Ω =1(－10), L =100(300) is chosen respectively. Excellent agreements are found, which shows the evidence of grid independence and high accuracy. Therefore,the results shown below are calculated with N =2048. In Fig. 1,we disply three branches of speed-amplitude bifurcation curveswhich comes from Euler model, KdV model and Choi's strong nonlinear model [26]. As expected, the difference between them becomes considerable when H becomes large. But the great coincidence of weakly nonlinear case proves their validity.

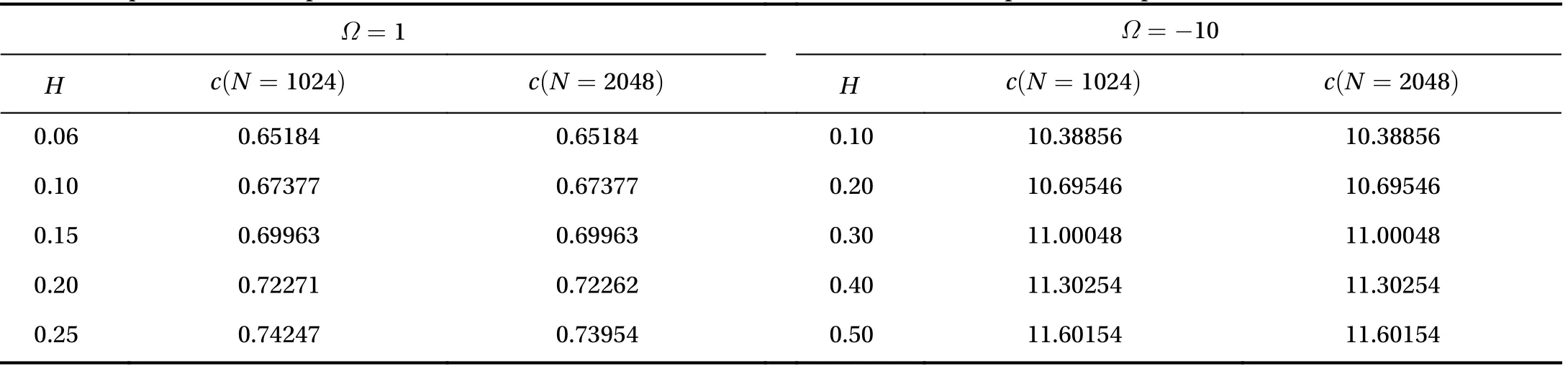
Table 1 A quantitative comparsion of the numerical simulations with different numeber of spacial mesh points.

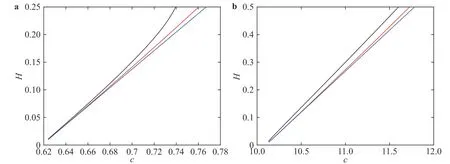
Fig. 1. A comparsion of three speed-amplitude bifurcation curves of solitary waves. Black: Euler model. Blue: KdV model. Red: Strong nonlinear model. In a:. In b:.

In the following part we briefly display some of the results from the KdV model and DNS. In all the examples, we exhibit our results in two special frames of reference. One is the frame moving with solitary waves so that trajectories coincide with streamlines, the other is the still frame in which φx→0 when |x|→∞.

When a constant vorticity exists, it is found that there are two types of streamlines in the moving frame of reference, which are open profile-shaped streamlines and closed streamlines respectively. The closed streamlines only exist under the condition that Ω and c have different signs. This coincides with our analysis of the stream function (16).

A t ypical result is shown in Fig. 2 with Ω =－10 and different values of H. We compare the wave profiles and particle trajectories based on the KdV model and DNS respectively. In Fig. 2a,H=0.1 and the KdV model provides a good quantitative description to the profiles and particle trajectories. The values of wave speeds are c ≈10.43 (KdV) and c ≈10.39(DNS) respectively and the computing time periods of the particle trajectories are [ 0,3],[0,3] and [0 ,23] from top to bottom. With H gradually increasing to 0 .3, the difference between the model and DNS cannot be ignored in Fig. 2b. The wave speeds are c ≈11.1( KdV) and c ≈11.0(DNS) with computing time periods are chosen [ 0,3], [ 0,3] and[0,10.5] from top to bottom.

To see the different flow structure clearly, we choose two typical results and exhibit their streamlines in the moving frame of reference in Fig. 3. In Fig. 3a, Ω =1, c ≈0.73. In this case, there are only open streamlines. In Fig. 3b, Ω =－10, c ≈11.6. When Ω and c have different signs, there could be a family of closed streamlines with a stagnation point inside. Calculation via Eq.(18) predicts the stagnation point is located at z ≈0.673, which is quite close to the DNS result z ≈0.7. Similar numerical result for periodic waves can be found in Refs. [19, 22]. This yields that there is a domain where particles are trapped, so they will move with the crest periodically. The corresponding particle trajectories in the still frame are shown in Fig. 4. In Fig. 4a, the linear shear current and solitary wave induce two flows in opposite directions. So the particles near the bottom are swept to the left by strong current. In Fig. 4b, the current near the bottom sweeps particles in front of solitary wave, where they have positive vertical velocity. After that they are exceeded by wave and then move downward, so periodic movements appear in this case.

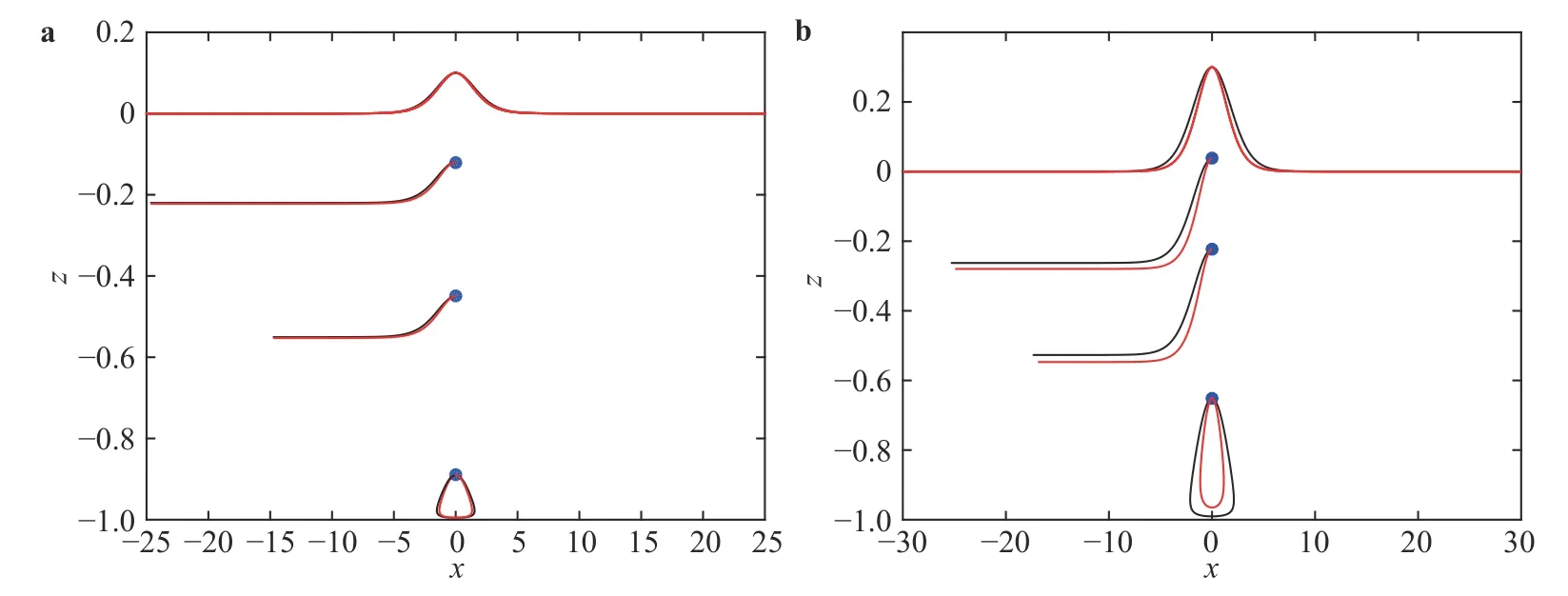
Fig. 2. Comparison of wave profiles and particle trajectories from the KdV model (red line) and DNS (black line). In both figures,. The blue dots represent the start positions of the particles..

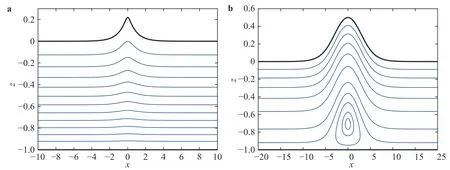
Fig. 3. Streamlines under the solitary waves in the moving frame. a. b. Different flow structures would appear depending on whether and have same or different signs.

Fig. 4. Particle trajectories in the still frame. The blue dots and profiles represent the initial positions and profiles at, the red ones and black ones represent the positions and profiles at and.

In this paper, we focused on particle trajectories beneath solitary waves interacting with a linear shear current. Using the asymptotic expansion, we obtained the KdV equation and the travelling wave solutions of the velocity field. On the other hand,we performed a DNS to the original Euler equations via conformal map to obtain the high-accuracy numerical solutions.When wave amplitude is small, asymptotic solutions coincide well with numerical solutions. We also found that there are two types of particle trajectories. When Ω and c have same signs, the streamlines in the moving frame are quite similar to the case without current. When Ω and c are of opposite signs, closed streamlines can be found in the moving frame which yields periodic motions in the still frame.

Acknowledgement

This work was supported by the Key Research Program of Frontier Sciences, Chinese Academy of Sciences (No. QYZDBSSWSYS015) and the Strategic Priority Research Program of the Chinese Academy of Sciences (No. XDB22040203). The author would also like to acknowledge the support from Chinese Academy of Sciences Center for Excellence in Complex System Mechanics.