The axisymmetric Rayleigh waves in a semi-infinite elastic solid

Ji Wng, Shoyun Wng, Longto Xie, Yngyng Zhng, Lili Yun, Jinke Du, Hn Zhng*

a Piezoelectric Device Laboratory, School of Mechanical Engineering and Mechanics, Ningbo University, Ningbo, 315211 Zhejiang, China

b Noise and Vibration Laboratory, Institute of Acoustics, Chinese Academy of Sciences, 100190 Beijing, China

K eywords:Axisymmetric Rayleigh wave Solid Propagation Velocity

ABSTRACT It is well-known that Rayleigh wave, also known as surface acoustic wave (SAW), solutions in semiinfinite solids are plane waves with signatory properties like the distinct velocity and exponentially decaying deformation in the depth. Applications of Rayleigh waves are focused on the deformation and energy in the vicinity of surface of solids and less loss in the propagation. A generalized model of Rayleigh waves in axisymmetric mode is established and solutions are obtained with cylindrical coordinates. It is found that the Rayleigh waves also propagate in the axisymmetric mode with slow decay in radius, confirming the existence of surface acoustic waves is irrelevant to coordinate system. On the other hand, the solutions can be treated as plane waves in regions far away from the source. Furthermore, the particle trajectory of axisymmetric SAW is a line with constant slope rather than the signatory ellipse in Cartesian coordinate case.

Rayleigh waves, also known as surface acoustic waves (SAW),are widely known and frequently utilized in various engineering applications such as earthquake engineering, acoustic wave devices, sensors, medical instruments, among others. In the beginning, Rayleigh wave solutions are given in Cartesian coordinates with plane wave assumptions [1]. The special features of Rayleigh waves such as the distinct velocity and exponentially decaying along the depth have generated a lot of interests and found many applications by taking the advantage of less loss in propagation. Recently, axisymmetric structures for SAW generation and propagation have been proposed and tested [2, 3], exhibiting a growing demand for analysis of SAW in such special structures. Driving by novel applications, it is found that the SAW mode in axisymmetric structures, though simple and natural as it is, has not been carefully investigated. Consequently,the features of axisymmetric SAW and advantages have to be presented to lead in-depth efforts in developing more creative technology and innovative applications.

In reality, seismic waves which are triggered by a point load near the earth surface, so does the ripples stirred by throwing a piece of small rock into a tranquil pond, because they all are axisymmetric surface waves with a circular wavefront. In comparison with planar surface waves, which are widely utilized in engineering, especially in the SAW devices which are essential in wireless communications, filters, sensors and so on [4-6], the axisymmetric surface waves are seldom focused by researchers.Currently, circular SAW devices based on axisymmetric surface waves are used to improve the transmission characteristics and loss notably in comparison to traditional rectangular architectures [2, 3]. Moreover, axisymmetric SAW is also used in the microfluidics such as the jetting of droplets by the focusing property of circular SAW [7, 8]. Furthermore, circular SAW devices can actuate the circular wave packets which can be used in acoustic tweezers to manipulate cells or particles [9, 10].

The research of axisymmetric surface wave was first studied by Lamb in 1904 [11], soon afterwards Lord Rayleigh discovered the planar SAW [1]. Because of the interest from the seismology,Lamb considered it as a classical elasticity problem that is to obtain the transient response to a time-harmonic load normal to the surface of the semi-infinite media and that is referred to as“Lamb's Problem” now. He transformed the wave equations of the potential function from Cartesian coordinates into cylindrical coordinates at first and then obtained the explicit expression of axisymmetric surface waves directly. Once the explicit solutions were obtained, the dynamic response can be obtained by the Fourier transformation obviously. The integral of the inverse Fourier transformation is difficult to calculate for generalized loadings, but Lamb found it can be solved approximately for normal point and line loads. After that, many other cases of different loadings were considered and other approximate approaches were developed by latter researchers. For example,Chao [12] solved a similar problem while the half-space solid has a point load that is tangential to the surface and Achenbach considered a more realistic problem with a buried point load in approximating the earthquake and solved it by the reciprocal method [13]. For more detailed description of this problem, it can be referred to popular textbooks of wave motion [14-20].

Although the explicit solutions of axisymmetric surface waves were found by Lamb and many transient response problems were studied by others, a systematic study with cylindrical coordinates and the comparison between axisymmetric surface waves and planar surface waves was not presented. Questions such as the velocity of both waves and differences of displacements are remaining to be answered. To provide detailed answers, the equations of the potential function of axisymmetric SAW in the cylindrical coordinate system were derived in a systematic manner and they were solved by the standard method which can be found in popular books on wave propagation[14-20]. After going through a standard procedure, we obtained the velocity and displacement solutions of axisymmetric SAW in a semi-infinite elastic solid with cylindrical coordinates. It is found that the axisymmetric SAW propagates with Rayleigh wave velocity, and the displacements are also decaying exponentially along the depth, proving the existence of axisymmetric SAW.

Governing equations and solutions of axisymmetric surface acoustic waves in cylindrical coordinates are derived as the beginning. We now consider that the axisymmetric SAWs propagate along radius and decay along the depth in a semi-infinite elastic solid z＞0 with cylindrical coordinates shown in Fig. 1.Owing to the axisymmetric property for this problem, the angular coordinate θ and the circumferential displacement component uθare neglected. As a result, the displacement vector can be simplified as

Using Helmholtz decomposition, we can introduce a scalar potential Φ and a vector potentialto simplify the problem [14]. With Eq. (1), we only need to retain component Hθin H, so the displacements can be decomposed into

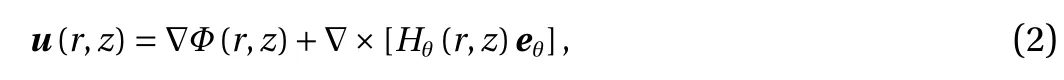
and Eq. (3) are simplified to

Equation (5) are the governing differential equation of axisymmetric surface waves. To obtain solutions, we also have the surface free boundary conditions

where the stress components are

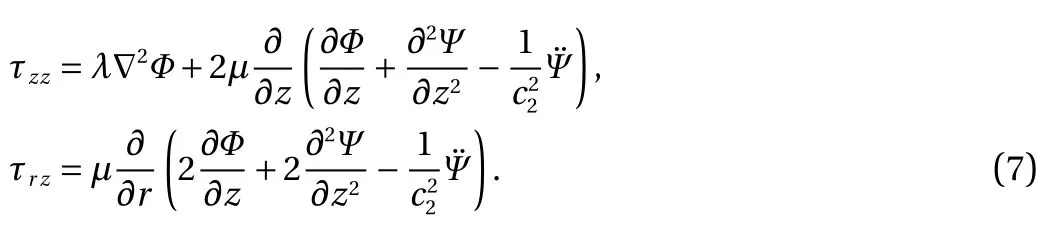
For convenience, the displacements of axisymmetric surface waves are also expressed by the potentials Φ and Ψ as

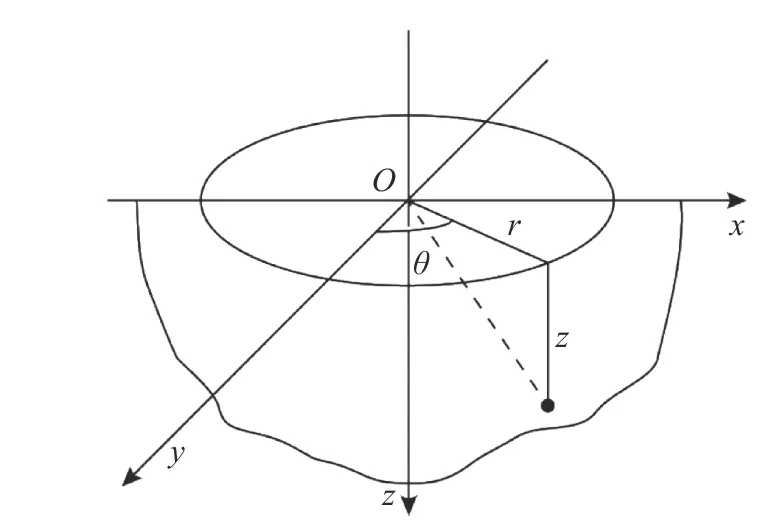
Fig. 1. A semi-infinite substrate with cylindrical coordinate.

Since the two equations in Eq. (5) are the same, we only need to solve one equation. With the method of separation of variables, we retained the following solution

where A is the undetermined constant, ω is angular frequency, α is decaying constant, and ξ is the wavenumber. Moreover, these three variables satisfy the relationis the zeroth-order Bessel function of the first kind. The zeroth-order Bessel function of the second kind Y0(ξr) is neglected because of its singularity at r =0, and the exponential function eαzis neglected because it is unbounded at z =∞. Similarly, we have

where B is the undetermined constant and β is decaying constant satisfying the relation

With these solutions, we can use the relationships between potentials, stresses, and displacements with the standard procedure for wave velocity and modes.

Then, the velocity and displacements of the axisymmetric surface waves are discussed. The substitution of Eqs. (9) and (10)into boundary condition (6) with the stresses expressed by Eq.(7) leads to

which is the same as Eq. (121) in Lamb's paper [11]. UsingEq. (12) becomes

which are the same as the Eq. (6.1.83) of surface acoustic waves in Cartesian coordinates from Graff [14] if one substitutes iξB with B in Eq. (13). The vanishing of the coefficient determinant in Eq. (13) gives the frequency equation for surface acoustic waves as

It is exactly the wave velocity Eq. (6.1.86) of surface acoustic waves, or Rayleigh waves, in Cartesian coordinates as given by Graff [14]. In other words, these two types of waves in different coordinate systems and waveforms travel with exactly the same velocity in the semi-infinite elastic solid.

Then we can compare the displacements of axisymmetric surface acoustic waves with the Cartesian coordinate solutions also. The amplitude rations of Eq. (13)

and the displacements become

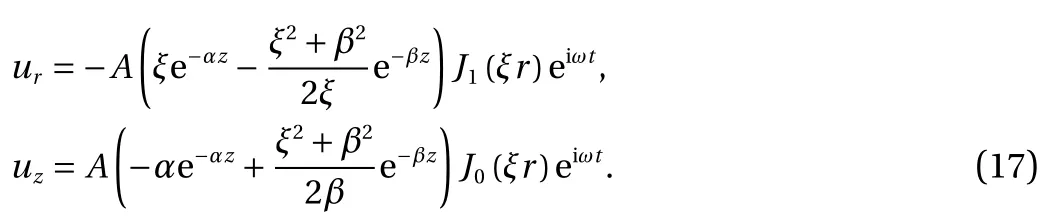
Introducing the wavelength λRby noting λR=2π/ξ and taking the real part of the displacements, we have the displacements in dimensionless form as

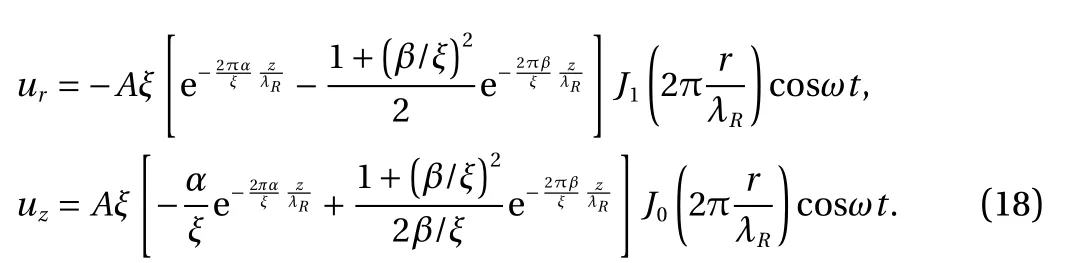
Now we calculate the displacements with ξ=2π, Aξ=1, and the Poisson's ratio ν=0.25. The displacements of Eq. (18) are shown in Figs. 2 and 3.

On the surface of the solid at z=0, Eq. (18) is reduced to

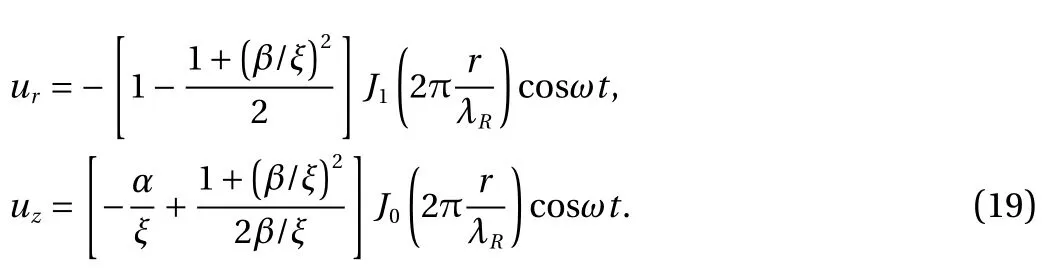
The envelops of the surface waves, which are constituted by two curves of Eq. (19) at ωt=0 and ωt=π, are plotted in Fig. 4 with a few curves in between. Different from the surface waves in Cartesian coordinates, the axisymmetric surface waves decay along the radial direction with Bessel functions. Furthermore,the orbit of a particle on the surface, which can be obtained by eliminating time in Eq. (19), is

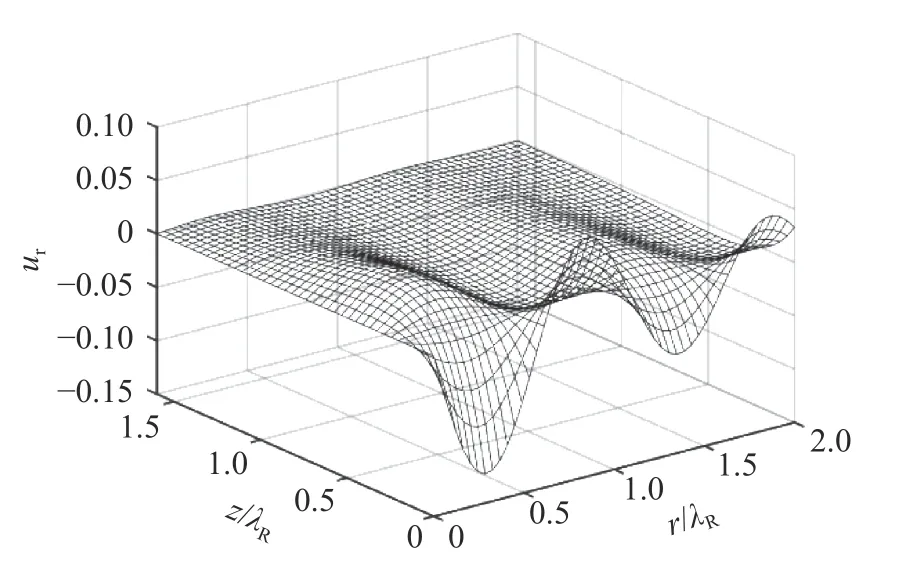
Fig. 2. Displacement ur vs. the normalized coordinate r/λR and z/λR.

where k is a function of r and z. With the time factor through cosωt, the trajectory of the particle on the surface is no longer a perfect ellipse, showing a notable difference between the two types of surface waves. Each particle now moves from one endpoint to another endpoint and then back to the original endpoint again along the line at different time, as shown in Fig.4. We now calculate the displacements along the depth at r/λR=5/4, resulting equation (18) reduced to

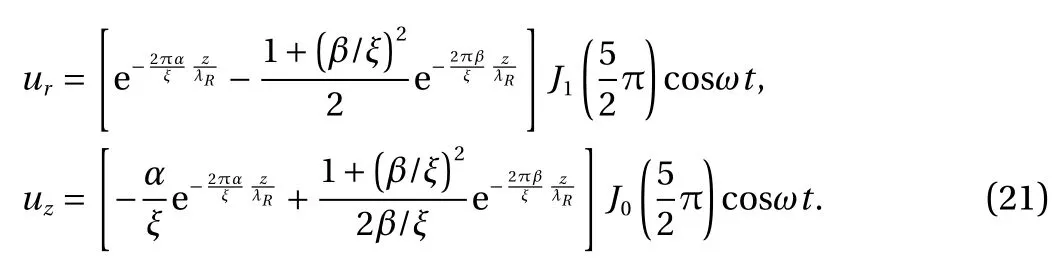
To compare the results with a similar case in Cartesian coordinates, normalized displacements with two Poisson's ratios ν=0.25 and ν=0.34 are plotted in Fig. 5. It is the same as shown by Graff [14], indicating that the displacements along the depth are the same for two types of surface waves. The displacement modes of the surface waves along the depth are shown in Fig. 6 with different time, and the displacements decaying along the depth signify the feature of surface acoustic waves. However, the particle orbit of the axisymmetric surface waves is still a line,which again differs from the surface waves in Cartesian coordinates.

Finally, we studied the axisymmetric surface waves in the far field. Strictly speaking, the wave velocity can be defined only by the function in the form of f (ξ(r－ct)). We can see clearly that displacements in Eq. (18) do not satisfy this condition. However,for the large radius r, Bessel functions can be expressed in the following asymptotic form

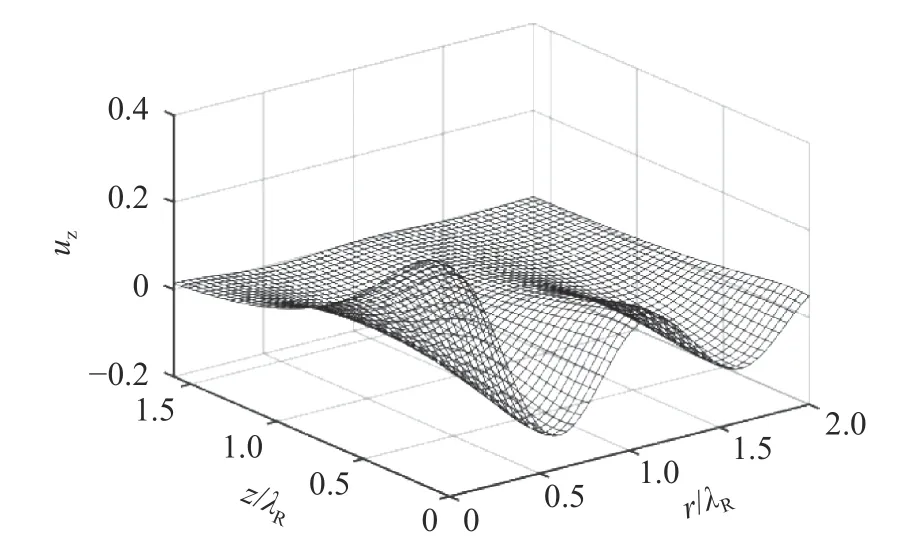
Fig. 3. Displacement uz vs. the normalized coordinate r/λR and z/λR.

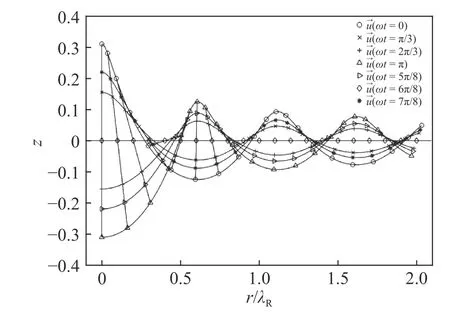
Fig. 4. The total displacement of surface waves at z=0 and the orbit of particles.

With this, we have

where

Using the basic identities of trigonometric functions, Eq. (18)become

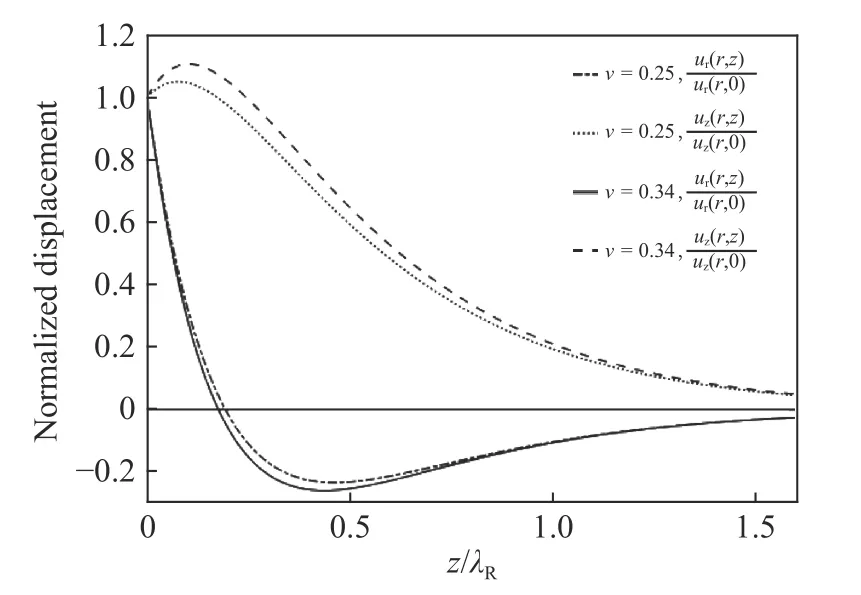
Fig. 5. Normalized displacements along the direction of depth.

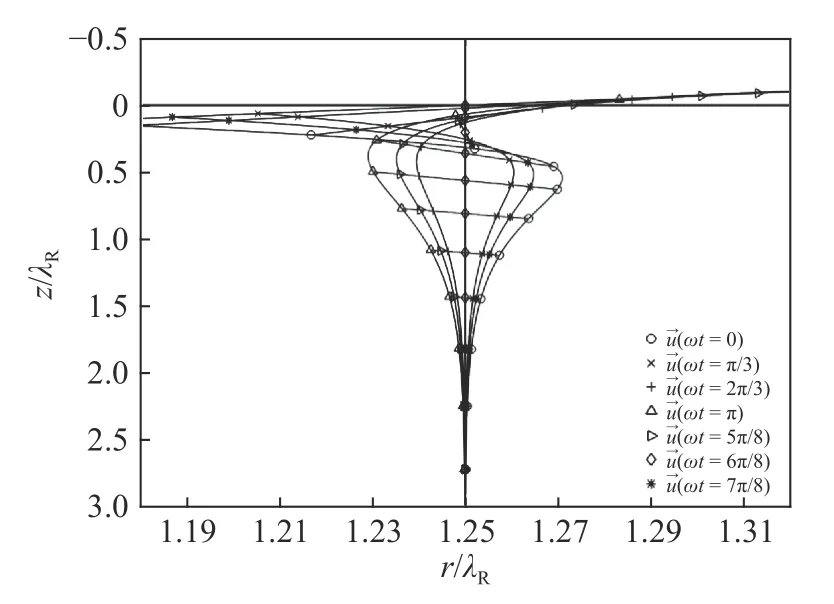
Fig. 6. The displacement of surface waves at and the orbit of particles.

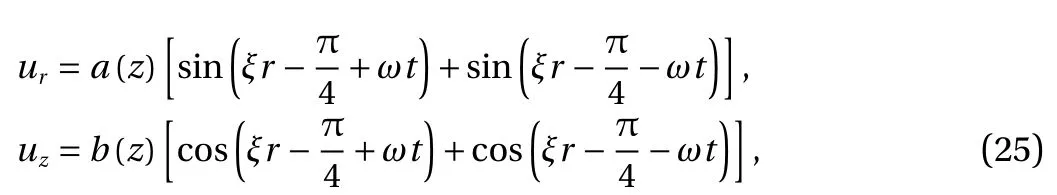
which are in the waveform of f (ξ(r－ct)) and are the superposition of one forward travelling wave with the one backward traveling wave with the wave velocity c=ω/ξ.Therefore, the axisymmetric surface waves exhibit the property of travelling waves. Furthermore, the displacements in the far field exhibit a r-1/2decaying, while it is an invariant in Cartesian coordinates. In fact, it can be explained from the density of the energy. When the axisymmetric surface waves travel from the source, the energy is distributed on the cylindrical surface where each finite area possesses the energy proportional to 1 /(2πr).Because displacements are proportional to the square root of energy, the displacements are proportional to r-1/2naturally. For a large radius, the axisymmetric surface waves can be considered as planar surface waves in a small range. This explains that we can use planar surface waves to approximate the axisymmetric surface waves in far field.

In summary, governing equations of axisymmetric surface waves were established by introducing two potential functions in cylindrical coordinates. Using the method of separation of variables, the equations were solved with traction-free surface boundary conditions. We have obtained the algebraic equation of the wave velocity which is same as that of Rayleigh waves in Cartesian coordinates. The displacements functions of axisymmetric surface waves were also obtained and the properties are examined. The displacements exhibit the exponential decaying along the depth as they are in Cartesian coordinates. However,the displacements of axisymmetric SAW also decay along the radius, implying the dilution of energy in the propagation. Furthermore, orbits of particles of axisymmetric surface waves are straight lines, which notably differ from the ellipses in Cartesian coordinates. Finally, the axisymmetric surface waves in far field were examined, which are the superposition of two travelling waves propagatng in opposite directions. Moreover, the displacements along radius are proportional to r-1/2in far field because of the increasing of the area of the wavefront and the axisymmetric surface waves are planar surface waves in far-field approximately.

Acknowledgement

This work was supported by the National Natural Science Foundation of China (JW: 11672142; HZ: 11972354 and 11772394), the National Key Research Initiative on Additive Printing (2017YFB1102900), and the K. C. Wong Magana Fund of Ningbo University.