Frame-indifference of cross products, rotations, and the permutation tensor
2020-06-06MaolinDu
Maolin Du*
Department of Civil Engineering, Sanjiang University, Nanjing 210012, China
Keywords:Pseudovector Cross product Improper transformation Handed coefficient Permutation tensor
ABSTRACT Under improper transformations, the traditional transformation laws for cross products, the permutation tensor, and rotations are incorrect. For a cross product, using a counter-example the left-hand rule is proved wrong. The unique rule for a cross product is the right-hand rule.Coordinate systems have handedness, while a cross product is frame-indifference. Since the permutation tensor is defined as a triple product including a cross product, the law for the permutation tensor is false. For a rotation, its pseudovector representation is incorrect, because the mirror is an auxiliary device to produce the virtual image rather than a new coordinate system or reference frame.
For complicated problems, coordinate transformations are helpful to simplify the analyses. There are two classes of orthogonal transformations. One is a proper transformation in which two coordinate systems have the same handedness. The other is an improper transformation in which the two coordinate systems have different handedness [1]. Since the transformation law for a cross product was different from the law for an ordinary vector, a cross product was defined as a pseudovector [2, 3].Similarly, the permutation tensor was defined as a pseudotensor. Rotating quantities such as angular velocities were also pseudovectors under mirror transformations. On many occasions, the "pseudo-" was omitted without caveats.Rigorously, the "pseudo-" was clearly stated, for example, moments or torques [4], angular velocities [5, 6], angular momentums [7-9], angular momentum densities [10, 11], vorticity vectors [12], Berry curvatures [13, 14], magnetic fields [15, 16],anapoles [17], effective spin-orbit couplings [18], and magnetooptic effects [19].
However, we find that the transformation law in traditional theory for a cross product is wrong; accordingly, a cross product is not a pseudovector and the permutation tensor is not a pseudotensor. For related problems, we demonstrate that the left-hand rule for cross products is incorrect and a rotation quantity is not a pseudovector.
Firstly, we prove the incorrectness of the traditional law.
Two rectangular coordinate systems, C and C′, have bases( e1, e2, e3) and (), respectively. If C and C′have different handedness, in traditional theory, the transformation law for the cross product of two vectors a and b was incorrectly in the form of (see for example in Ref. [1], p125)

where a repeated index denotes summation over all values of that index, i.e., the Einstein summation convention is used (the same below). Since Eq. (1) is different from the transformation law for an ordinary vector, a cross product was wrongly defined as a pseudovector.
We derive the correct transformation law as follows.
Theorem 1. Let ( e1, e2, e3) be the basis of a rectangular coordinate system C, and () the basis of a new rectangular coordinate system C′. The transformation for the cross product of two vectors a and b is

Proof. Assuming that v is an arbitrary vector, we have [20]


Equation (2) holds under both proper and improper transformations. Consequently, the traditional theory Eq. (1) does not hold.
Secondly, using a counter-example, we prove that the lefthand rule for cross products is incorrect.
In a left-handed rectangular coordinate system of basis ( e1,e2, e3), a left-hand rule [21, 22] for a cross product was specified as

where i , j, k is a cyclic permutation of 1, 2, 3. Due to the false rule Eq. (6) in left-handed coordinate systems, the incorrect formula for the cross product of two vectors a and b was

where a=a1e1+a2e2+a3e3, and b=b1e1+b2e2+b3e3. The component form of Eq. (7) is

Fig. 1. Counterexample. A left-handed coordinate system has basis(). The moment of a force about point O is,which is frame-indifference. However, if the left-hand rule Eq. (6) is used, a wrong value, , is obtained

where i, j, k is a cyclic permutation of 1, 2, and 3.
Using a counter example, the incorrectness of the left-hand rule Eq. (6) can be proved. Physical quantities, such as angular velocities, the moments of a forces, angular momentums, magnetic fields, are frame-indifference. However, these quantities were mistaken for pseudovectors. Let a left-handed coordinate system have basis ( e1, e2, e3), as shown in Fig. 1. Consider a force F=e1acting on point A as shown in Fig. 1. Let r =e2be a vector directed from point O to point A. By using the left-hand rule for cross products Eq. (6), the moment of a force F about point O is
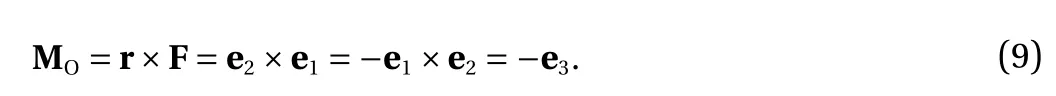
Physically, the moment of force F about point O is e3/=-e3.Consequently, the left-hand rule for cross products in a lefthanded coordinate system does not hold. The reason behind the incorrectness is that the cross product is objective and frame-indifference.
The incorrectness of Eq. (7) can also be proved by the above example.
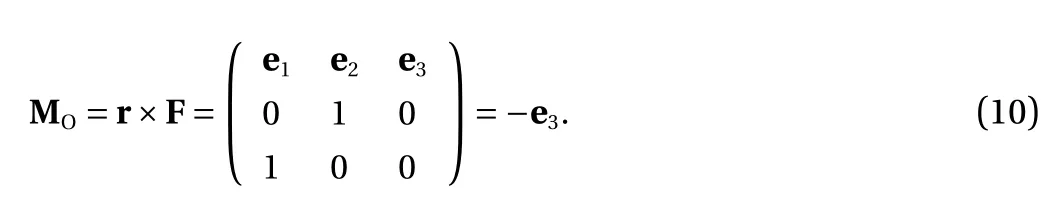
Equation (10) shows that the left-hand rule for cross products is wrong. Therefore, the right-hand rule is the unique rule for a cross product.
Thirdly, under the unique rule, we derive the correct formula for vector products. For convenience, we define a handed coefficient for a rectangular coordinate system

With the handed coefficient, a cross product can be determined correctly as follows.
Theorem 2. Assuming that ( e1, e2, e3) is the basis of a rectangular coordinate system, the cross product of two vectors a and b is obtained by
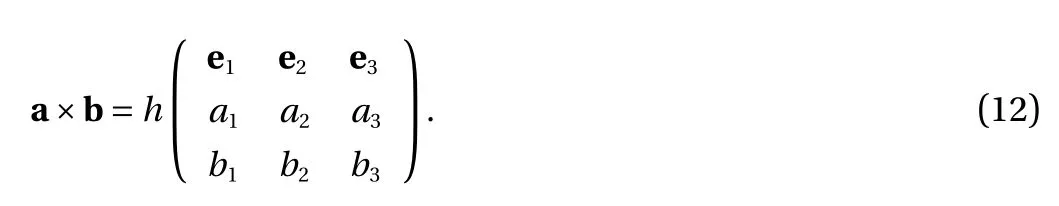
Proof. Using Eq. (11), we have
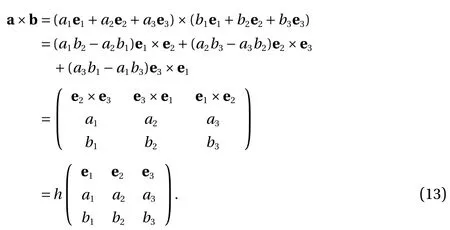
Fourthly, we consider the permutation tensor including a cross products. The permutation tensor is defined as [1]

The permutation tensor is also called permutation symbol,alternating symbol, Levi-Civita symbol, and antisymmetrical tensor [1,23].
Theorem 3.The permutation tensor is an ordinary tensor
Proof.

Equation (15) shows that the permutation tensor is an ordinary tensor. Since the permutation tensor includes a cross product, it was incorrectly represented by

Corresponding to Eq. (12), the following theorem gives the correct representation of the permutation tensor.
Theorem 4.
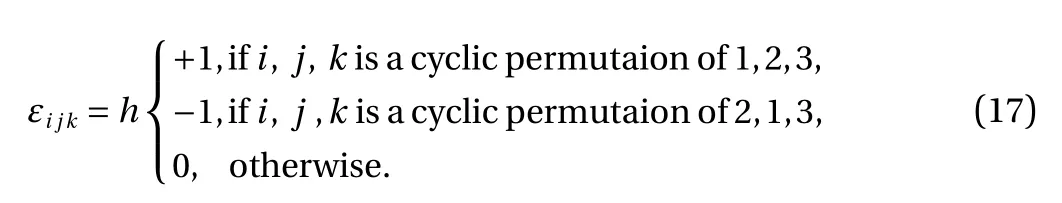
Proof. By using Eqs. (12) and (14), Eq. (17) is proved.
Finally, we consider the representation of a rotation. As shown in Fig. 2, according to the right-hand rule the rotations R and R′are represented by vectors V and V′, respectively. If R′is a mirror image of R, the corresponding vector V′is not the image of V. For this reason, the vector representing a rotation was wrongly defined as a pseudovector based on a mirror transformation by mistake.
We illustrate that a mirror is not a coordinate system or observer. In fact, the mirror is an auxiliary device to create the image R′. If the image R′and the mirror are replaced with a real rotation R′, the same picture of two objects R and R′can be taken by a camera before and after the replacement. The camera is the only observer or coordinate system.
A coordinate transformation means that only one object is considered in two coordinate systems. For example, the rotation R is in coordinate systems, xyz (righthanded) and XYZ (lefthanded), as shown in Fig. 3.
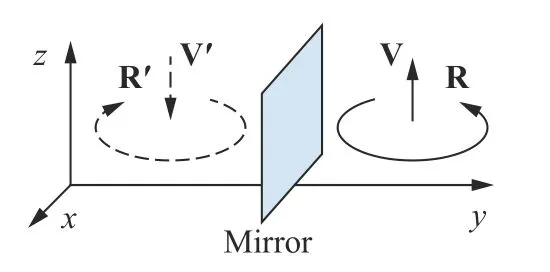
Fig. 2. Two symmetric objects and in one coordinate system
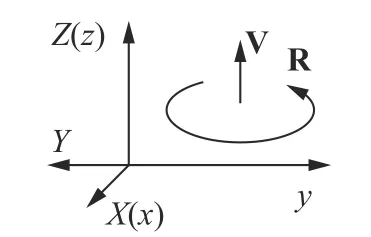
Fig. 3. One object, rotation, is in two coordinate systems. XYZ and xyz are left-handed and right-handed coordinate systems, respectively
In summary coordinate systems have handedness, while a cross product is frame-indifference. Coordinate systems are conveniently characterized by a handed coefficient. The traditional transformational law for cross products under improper transformations was wrongly derived, because the left-hand rule for cross products is incorrect. The right-hand rule is the unique rule for cross products. Consequently, a cross product is an ordinary vector rather than a pseudovector. Since the permutation tensor is defined as the triple products including a cross product,the permutation tensor is an ordinary tensor.
In representing a rotation by a pseudovector, a mirror was confounded with a coordinate system before. In fact, the image of a rotation is a new virtual rotation, which is not the original rotation in a new coordinate system. Therefore, a vector representing a rotation is not a pseudovector.
Acknowledgement
The author is grateful to the support by the National Natural Science Foundation of China (No. 51978166) and the Research Fund of Sanjiang University (No. 2018SJKY005).
杂志排行
Theoretical & Applied Mechanics Letters的其它文章
- Editorial: Computational granular mechanics
- Construction of irregular particles with superquadric equation in DEM
- Prediction on dispersion in elastoplastic unsaturated granular media
- A block particle coupled model and its application to landslides
- Modified virtual internal bond model based on deformable Voronoi particles
- Modeling of deformation processes in rock massif in the vicinity of underground goafs considering the formation of discontinuity zones
