强度折减法在超大直径顶管群抗浮稳定分析中的应用

赵津磊， 肖 婷， 周亚军， 王海俊

(1. 江苏省水利勘测设计研究院有限公司， 扬州 225127； 2.扬州大学广陵学院， 扬州 225000)

顶管是继盾构之后发展起来的一种暗挖式施工方法，常应用于管道需穿越公路、铁路、河流的工程中。在顶管穿越河流的工程中，管道易发生上浮。这是由于顶管水下段上覆土一般较薄，在一些特殊断面还可能出现超浅覆的情况。因此，在水下顶管的设计中，进行顶管抗浮稳定验算是十分必要的[1-2]。

传统顶管抗浮稳定验算方法为一种重力分析模式，管道直径范围内上部土体和管道的自重发挥抗浮作用，两者质量之和与浮力之比作为反映结构的安全系数。该验算方法简单实用，但考虑的影响因素单一，没有考虑土体的土拱效应。另外，在对超大直径顶管群进行抗浮稳定分析时，传统算法无法考虑顶管间的相互影响及大直径顶管的尺寸效应[3-6]。

强度折减法最初由Zienkiewicz等[7]于20世纪70年代提出，并成功运用于边坡稳定研究，该方法通过折减土体的参数使土体达到极限失稳状态，可得出安全系数及潜在滑动面。在运用强度折减理论进行边坡稳定分析时，关于极限失稳的判据一直是学者们关注的热点，也是争议较多的一个问题。赵尚毅等[8]认为有限元计算的收敛性可作为边坡失稳的判据，并研究了安全系数大小与所采用屈服准则的关系。栾茂田等[9]认为以有限元计算的收敛性作为失稳判据是不合适的，分析指出广义塑性应变和塑性开展区作为失稳判据较为合理。刘金龙等[10]考查了目前常用的失稳判据，分析得出特征部位位移的突变性或塑性区的贯通性较适合作为失稳判据。

前人研究主要集中在强度折减法在边坡稳定分析中的应用情况以及关于失稳判据的讨论，而关于强度折减理论在顶管稳定分析中的应用的研究较少，相关失稳判据的讨论更鲜有报道。鉴于顶管抗浮稳定分析中，传统重力分析模式在解决群管及超大直径顶管问题中的局限性。有必要将强度折减法应用到超大直径顶管群的抗浮稳定分析中，并深入分析合理的失稳判据，以期为管道的抗浮稳定研究提供借鉴。

1 基本原理

1.1 传统管道抗浮分析方法

在传统管道抗浮分析方法中，抗浮安全系数定义为抗浮效应与上浮效应的比值。抗浮效应包括管道自重和管道直径范围内上部土体有效重力：

W管=π(R2-r2)γc

(1)

G土=2γshR

(2)

式中：γc为管道重度；R为管道外径；r为管道内径；γs为土的浮容重；h为管道埋深。

上浮效应为管道所受浮力，即管道排开水的质量：

F浮=πR2γw

(3)

式(3)中：γw为水的重度。

抗浮安全系数表示为

F=(W管+G土)/F浮

(4)

1.2 有限元强度折减法

强度折减系数定义为岩土材料所具有的最大抗剪强度与固定外荷载作用下土体内部实际剪应力之比。基本原理是将岩土材料的黏聚力c和内摩擦角φ同步进行折减，折减后的参数重新参与计算，然后进行失稳判别，若为稳定状态则继续进行折减并重新计算，若为失稳临界状态则终止计算，此时的折减系数Fs即为安全系数。岩土材料折减后的黏聚力c′和内摩擦角φ′表示为

c′=c/Fs

(5)

φ′=arctan(tanφ/Fs)

(6)

强度折减法无需事先假设破坏面的位置和形式，且可获得岩土材料动态破坏过程，可用于破坏模式和稳定性分析。

2 工程算例概况

2.1 工程概况

工程算例为位于江苏省无锡惠山区的西直湖港北枢纽，该工程中顶管需穿越京杭运河与京沪铁路。顶管采用内径为4 m的超大直径顶管，且为6根顶管平行布置，顶管间中心距为10.3 m，净距为5.62 m。顶管壁厚为0.34 m，混凝土强度等级为C50。顶管穿越的土层为软塑-可塑粉质黏土，土层的具体材料参数如表1所示。

表1 材料参数Table 1 The material parameters

2.2 分析模型

根据工程资料，选取管道埋深较浅的断面(管道中心距河底7.34 m)建立二维有限元模型如图1所示，模型宽300 m、高75 m。全面考虑管片混凝土结构与土体之间的接触特性，采用基于Coulomb摩擦定律的硬接触。分析中模型两侧施加水平位移约束，底部固定位移约束，顶面为自由面。

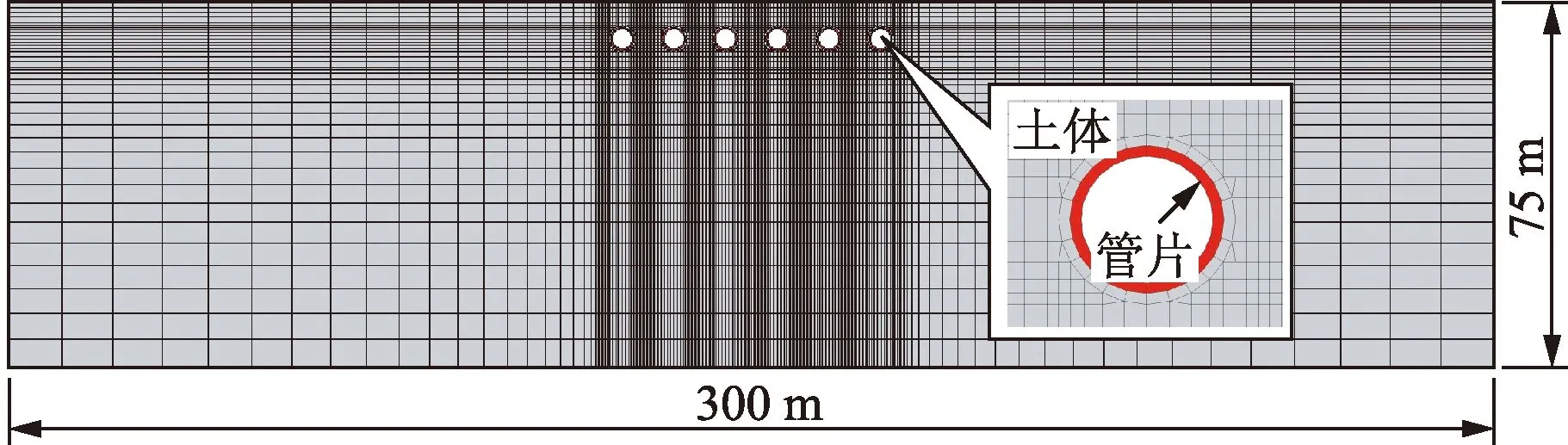
图1 有限元网格Fig.1 The finite element mesh

3 结果与分析

考虑到失稳判据在强度折减法中的重要性，为分析强度折减理论在超大直径顶管群抗浮稳定分析中应用的可行性，首先进行合理失稳判据的研究。研究将通过两种方案进行，分别是单管和六管并行。六管并行方案中管间净距首先采用5.62 m，然后进一步分析管间净距增大至11.24 m和缩小至2.81 m两种情况。

由于弹塑性有限元计算的收敛性受多种因素影响，在边坡稳定分析中，以数值计算的收敛性作为土体失稳判据的合理性受到了质疑[8]。在运用强度折减法进行顶管群抗浮稳定分析过程中，若以数值计算的收敛性作为土体失稳判据，则不同方案下得到的抗浮安全系数接近6.0，个别工况甚至超过了6.0。而运用传统算法[式(4)]分析本算例得到的抗浮安全系数为2.02。可以看出，以数值计算的收敛性作为土体失稳判据获得的抗浮安全系数明显偏大，不适合作为顶管抗浮分析中的失稳判据。因此，将重点分析塑性区贯通性和特征点位移突变性在顶管抗浮稳定分析中作为失稳判据的合理性。

3.1 单管方案

根据强度折减法的原理，强度折减系数自1.0开始逐渐增大，并利用折减后的c′、φ′值重新进行数值计算，记录不同折减系数下顶管上部地表的位移及塑性区的分布情况。

限于篇幅，仅列出了部分典型结果。图2为单管方案中，折减系数由1.90增大至2.30时地表竖向位移的分布情况。图3为折减系数分别为2.10、2.15、2.20时塑性区的分布情况。

图2 单管方案中不同折减系数下地表位移Fig.2 The surface displacement under different reduction factors in single pipe scheme

折减系数为2.10以内时，地表变形规律基本一致，具体表现为顶管中心上方地表位移最大，两侧位移逐渐变小。而且折减系数越大，地表最大竖向位移量越小，这是由于相同上浮力作用下，随着折减系数的增大，顶管顶部土体塑性区域越来越大，顶管上部土体逐渐呈现向两侧流动的趋势，而向上变形趋势变缓。当折减系数达到2.10以上时，地表竖向的变形规律发生突变，地表最大变形位置不再是顶管中心正上方，而是在顶管中心线两侧。结合图3可以看出，当折减系数为2.15时，顶管顶部土体塑性区域已接近贯通地表，折减系数为2.20时塑性区已完全贯通，塑性区贯通意味着该区域土体无法继续承受荷载，此时为失稳状态。

分析可知，单管方案中若以地表位移发生突变为失稳判据，则安全系数Fs取2.15；若以塑性区贯通为判据，则安全系数Fs取2.20。综合两种判据，从偏安全的角度Fs取2.15较为合适。相同条件下，通过式(4)获得的抗浮安全系数为2.02。传统算法获得的安全系数稍低一些，这可能是由于传统算法中抗浮效应仅考虑了管道自重和上部土重的原因。总体来看，强度折减法与传统算法获得的安全系数基本一致，这说明强度折减法可用于顶管抗浮稳定的分析。而且通过强度折减法可获得上浮力作用下，顶管失稳时，土体潜在破坏面的形式如图3所示。

3.2 六管并行方案

图4为六管并行方案中，管间净距为5.62 m时，折减系数从2.30增至2.50时地表的竖向位移情况。图5为折减系数分别为2.40和2.45时塑性区的分布情况。

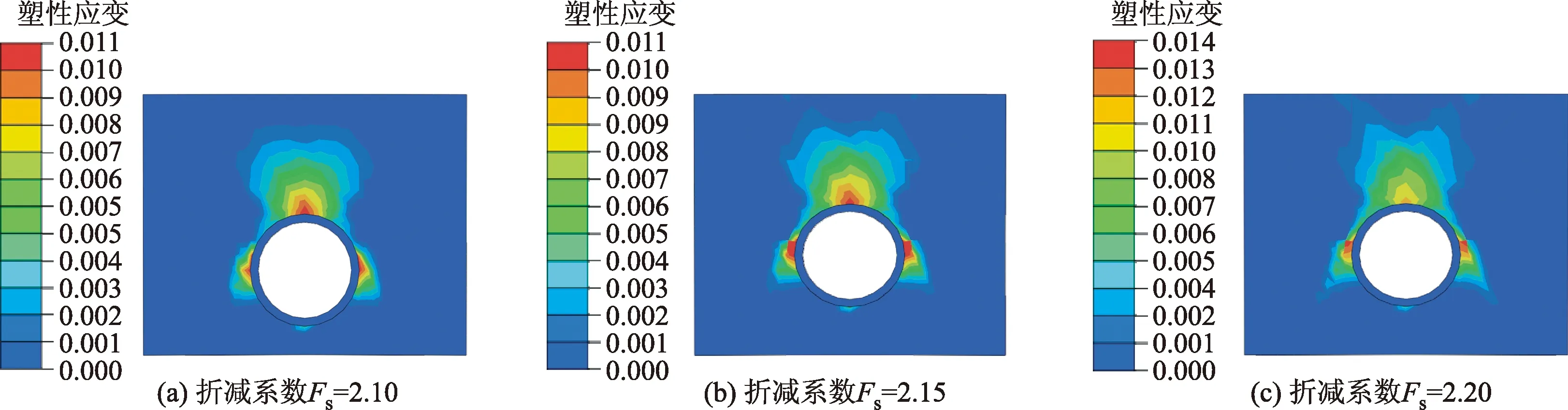
图3 单管方案的塑性应变云图Fig.3 The plastic strain nephogram in single pipe scheme

图4 六管并行方案的地表位移Fig.4 The surface displacement in six-pipe parallel scheme

不同折减系数下，地表竖向变形规律基本一致，群管中部变形最大，两侧逐渐变小。在折减系数为2.45时，群管左右最外侧顶管上部地表变形发生突变，两突变点之间的地表变形迅速增大，而两突变点外侧地表变形迅速减小，如图4(b)所示。结合图5可以看出，折减系数为2.45时，群管上部土体塑性区出现贯通地表的情况，位置为最外侧两顶管顶部，贯通带向群管中心倾斜。发生塑性贯通后，塑性贯通带内侧土体在中部群管上浮力的作用下竖向变形将突增。而且塑性贯通带外侧土体，在塑性区的隔离下，竖向变形将锐减。

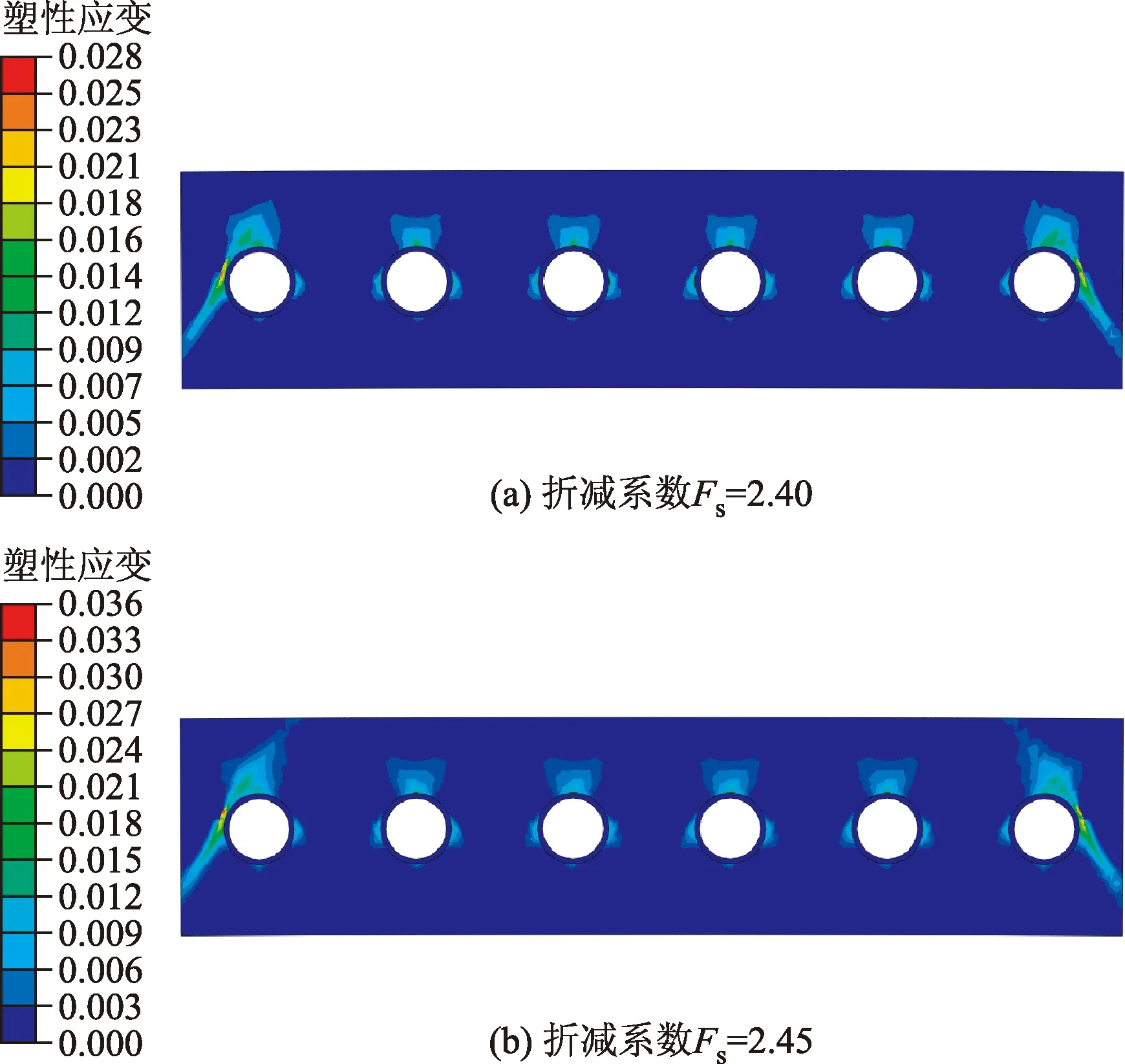
图5 六管并行方案的塑性应变云图Fig.5 The plastic strain nephogram in six-pipe parallel scheme

在该方案中，以地表位移发生突变和塑性区贯通两种判据得出的安全系数均为2.45，稍大于单管方案下的安全系数。初步分析认为，群管方案中，群管可视为一个整体，在上浮力作用下群管对上部土体形成一面积较大的力，顶管群上部土体协调变形，不易产生塑性区；而单支顶管在上浮力作用下对上部土体的作用面积小，更易使土体发生塑性变形。

3.3 群管间距的影响

利用西直湖港北枢纽中群管的设计参数，分别将群管间净距增大至11.24 m、缩小至2.81 m。同样综合运用地表位移突变性与塑性区贯通性两种判据，对群管在上浮力作用下的稳定状态进行判断。其中，群管间净距增大至11.24 m的方案，通过分析得出的群管抗浮安全系数与原设计中管间净距为5.62 m的方案基本一致，为2.45左右，并且地表位移分布规律及塑性区的发展过程也基本相同。因此，对于群管间净距增大至11.24 m的情况，这里不再作过多地讨论。值得注意的是，当群管间净距缩小至2.81 m后，综合地表变形突变及塑性区分布判断得出的安全系数仅为1.85左右，与原设计方案的安全系数相比显著减小。图6为群管间净距缩小至2.81 m后，在折减系数为1.85时，塑性区的分布情况。由图6可以看出，最先出现塑性区贯通地表情况的位置仍然为最外侧两顶管的上方，与原设计方案基本一致。不过群管间净距缩小至2.81 m后，群管之间的土体也出现了贯通的塑性区。也就是说，群管间距变小后不仅使群管整体安全系数大幅减低，同时也改变了土体潜在的破坏形式。

图6 六管并行间距缩小方案中折减系数为1.85时塑性区的分布情况Fig.6 The plastic strain zone when the reduction factor is 1.85 in six-pipe parallel scheme with spacing reduction

该工程原设计方案中，顶管外径为4.68 m，原设计方案中顶管间净距为5.62 m，顶管间净距为顶管外径的1.2倍。管间距缩小一倍后，顶管间净距为2.81 m，顶管间净距为顶管外径的0.6倍。根据上述分析可知，从群管抗浮稳定角度，原设计方案中群管间距是较为合理的，顶管间净距不易小于顶管外径。

4 结论

以江苏省西直湖港北枢纽为工程背景，深入研究了强度折减法在分析群管抗浮稳定中的可行性以及合理的失稳判据。得出的以下结论。

(1)强度折减法用于群管抗浮稳定分析是可行的，综合分析群管上方地表的位移以及塑性区分布情况可得出合理的安全系数，而以数值计算收敛性作为判据得出的安全系数明显偏大。

(2)与传统方法相比，运用强度折减法不仅可得到合理的安全系数值，而且可直观得到群管上方土体的变形以及塑性区分布情况，由塑性区分布可知，群管方案中易最先发生失稳破坏的位置为群管两端。

(3)群管间距过小不仅会使群管抗浮安全系数大幅降低，而且会改变土体潜在的破坏形式，具体工程中合适的群管间距应根据顶管尺寸及地质条件综合判断。

以上结论均基于平面应变情况下的二维分析结果，所得出的结论在三维情况下的适用性还有待于更进一步的研究。