城市浅埋小净距隧道合理净距研究

唐启童， 胡运春， 陈文宇， 晏启祥

(1. 西南交通大学交通隧道工程教育部重点实验室， 四川成都 610031； 2. 中铁隆工程集团有限公司， 四川成都 610045)

小净距隧道是指两隧道之间夹岩的最小宽度小于分离式隧道最小净距值，该最小净距与围岩等级有关[1]。与分离式隧道不同，小净距隧道中某一洞室的开挖都将改变另一洞室附近的应力场，即双洞施工存在相互影响[2]。在一般情况下，这种影响处于都较低水平，只有当净距小于某特定值后，这种影响才会迅速增大，使围岩的稳定性大幅降低，给施工过程带来巨大风险，通常将该特定值称为合理净距。

围绕小净距隧道的合理净距已有不少的研究成果[3-6]，但这些研究都是将开挖后的支护效应考虑在内，使开挖后的围岩应力仅部分释放，双洞开挖的相互影响无法达到最大，使得到合理净距欠缺一定的安全性。本文将以济南市玉函路城市小净距隧道为研究背景，建立三维有限元数值模型，仅考虑隧道开挖效应，对成洞后的地层应力、位移结果进行对比分析，提出该城市浅埋小净距隧道合理净距的取值方案，为类似小净距隧道的设计施工提供参考依据。

1 工程概况

济南市玉函路隧道工程北起顺河高架路南端南至英雄山路高架路北端，全长3.26km，是济南市快速路网规划系统的重要组成部分。该隧道分为明挖段和暗挖段，暗挖段贯穿城市繁华地区，采用小净距双隧道设计，两隧道间距3～5m，埋深8～11m，为五心圆断面，是浅埋小净距隧道。地层属Ⅴ级围岩，从上至下依次为填土、坡洪积成因的湿陷性黄土、黏性土及碎石，下伏奥陶系石灰岩，地质条件较差。地下水类型有第四系松散岩类孔隙水、灰岩岩溶裂隙水，但水位较低，均处于结构下方。本文将基于该城市小净距工程，通过研究不同净距下开挖形成毛洞后引起的地表沉降、洞周水平位移及Mises等效应力的变化规律，提出合理净距的取值方案。

2 数值模型

2.1 模型尺寸

玉函路小净距隧道断面形式为五心圆，最大跨度B为9.732m，高度H为8.21m，埋深为10m。为减小边界效应的影响，隧道外轮廓与模型左、右、下边界的净距均取为3B(即30m)，整体模型总宽度将随隧道间净距不同而发生变化，模型高度为48.21m，长度为40m，横截面尺寸见图1。

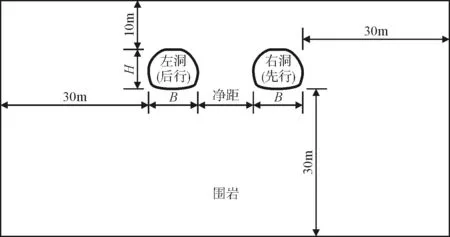
图1 模型横断面尺寸(单位:m)

2.2 参数选取及边界条件

围岩设置为单一围岩，采用D-P塑性本构，用三维实体单元模拟，围岩相关参数的取值见表1。由于本文仅对隧洞开挖后围岩的二次应力状态进行分析，因此未考虑支护结构的作用。模型的整体网格如图2所示。模型上边界设置为自由边界，其余边界分别约束其法向位移。

表1 模型材料参数

2.3 施工过程模拟

施工方法采用台阶法，上台阶高度为2m。利用单元的钝化功能，模拟掌子面前方土体的开挖，每次开挖进尺为2m，每个隧道共分成20个施工进尺。该模型中右洞先行开挖，而左洞掌子面落后右洞6m(即三个进尺长度)距离(图3)。

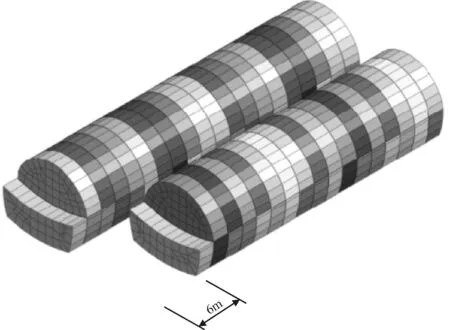
图3 掌子面范围内土体开挖示意

2.4 模型工况

考虑最大跨度B与隧道净距的关系，本模型中隧道净距共选取了5种工况：0.2B、0.4B、0.6B、0.8B和1.2B，并添加仅单洞开挖的工况。通过将五种小净距工况和单洞开挖的工况进行综合对比分析，保证提出净距方案的合理性。

2.5 监测断面及洞周测点布置

考虑到边界效应的存在，选取模型隧道段1/2位置处的横断面作为监测断面。在隧道开挖全部完成后，对该断面上的地表竖向位移以及洞周位移、应力的分布情况进行对比分析，其中左右洞洞周测点依照图4进行布置。单洞开挖时，洞周测点排列顺序与左洞相同。

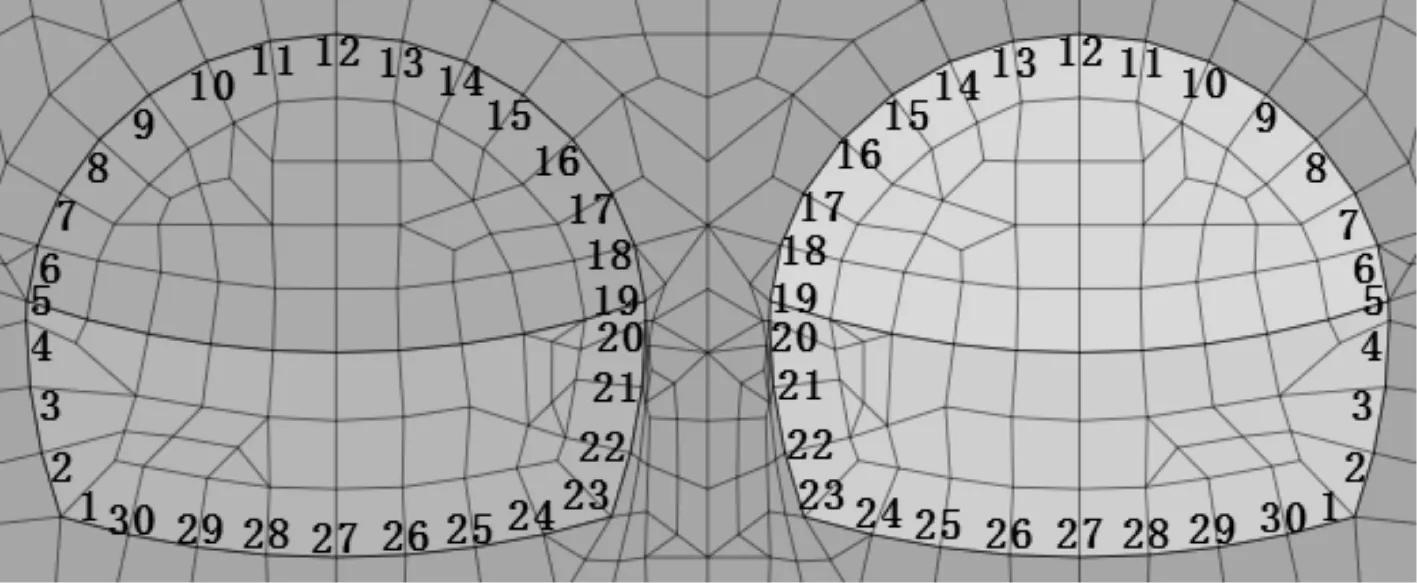
图4 洞周测点分布

3 计算结果分析

3.1 地表竖向位移

城市浅埋隧道通常下穿城市繁华地段，对于施工期间地表沉降的控制有着严格的要求。不同净距下的地表沉降计算结果见图5。

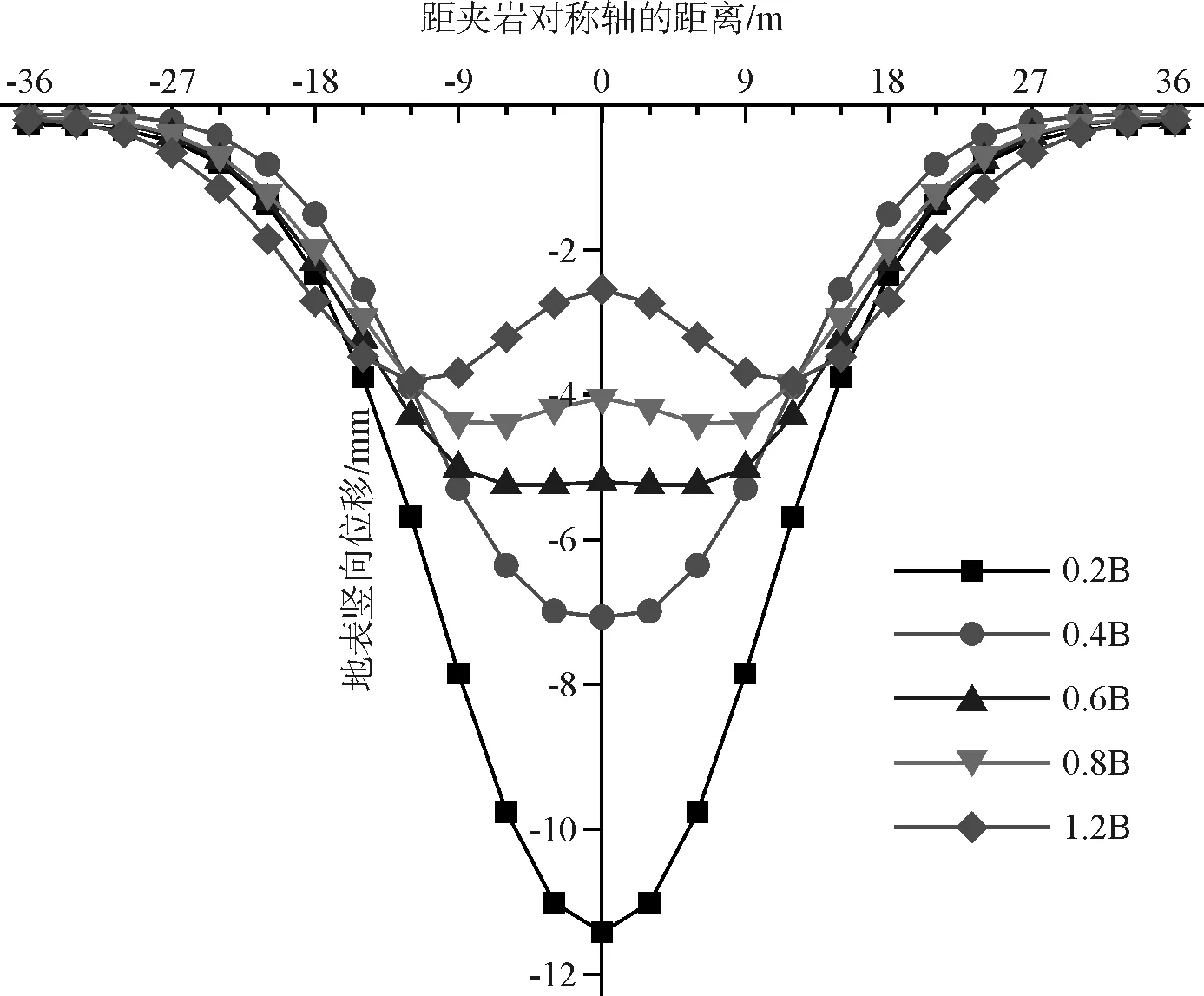
图5 不同净距下的地表沉降曲线

从图5可以看出，地表沉降曲线的形状满足左右对称；随着两隧道之间净距的增大，地表沉降值总体上呈减小趋势。当净距大于0.6B时，地表沉降曲线表现为“双槽形”，最大沉降发生在两隧道中心在地表的投影处；反之，则最大地表沉降发生在夹岩对称轴处，地表沉降曲线为单一的沉降槽。

为更清晰地说明地表沉降与净距的关系，绘制了地表最大沉降-净距关系曲线(图6)。根据图6的曲线能够看到，地表最大沉降随着净距的增大逐渐减小且趋于平缓。当净距与跨度之比超过0.6时，地表最大沉降随净距的变化非常缓慢，沉降值的大小也接近单洞开挖的结果，可以认为此时两隧道之间的相互作用已处于较低水平。当净距达到1.2B时，开挖产生的地表最大沉降与单洞开挖的结果几乎一致。

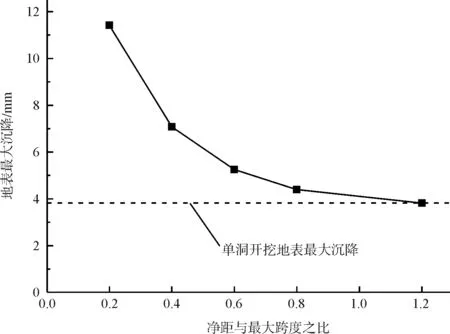
图6 地表最大沉降与净距的关系

3.2 洞周水平位移

玉函路隧道是水平方向上的小净距隧道，左右洞的先后开挖对洞周位移的影响将主要集中在水平方向上。对不同净距下左右洞洞周各测点上水平位移曲线(以向夹岩处移动为正)见图7、图8。

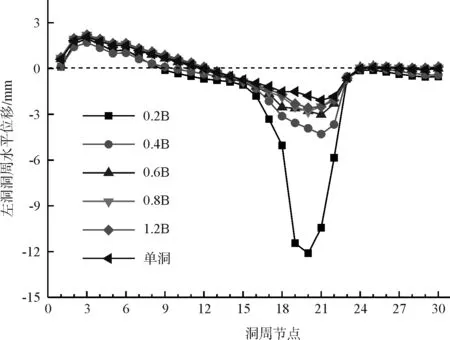
图7 不同净距下左洞洞周水平位移

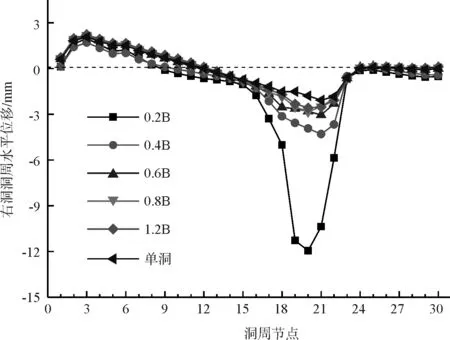
图8 不同净距下右洞洞周水平位移

由图7、图8可知，左右洞洞周在同一测点处水平位移相差不大，最大仅相差0.2mm；净距改变对洞周水平位移的影响范围主要集中在17～22号测点，其余各测点的水平位移随净距的改变几乎不发生变化；在净距从0.2B增大至0.6B的过程中，17～22号测点的水平位移迅速减小，当净距超过0.6B后，净距变化对17～22号测点的水平位移的影响已非常微小，且此时洞周水平位移曲线与单洞开挖的结果基本一致。

结合图4可以看出，17～22号测点均位于夹岩附近，其中变化最大的19～21号测点更是集中在夹岩中部。由此可见，当净距小于0.6B时，净距的改变对洞周水平位移的影响部位主要集中在夹岩中部附近；净距超过0.6B后，随着净距继续增加，夹岩的水平位移基本保持不变。

3.3 洞周Mises等效应力

Mises等效应力是判断材料是否达到塑性的指标，当材料某点处的Mises等效应力超过某规定值时，该点便进入塑性状态。对于隧道开挖过程，围岩Mises等效应力过大将使其达到屈服，自承能力大幅降低，严重时可能引起围岩失稳，对施工作业的安全造成极大影响。不同净距下左右洞洞周各测点上Mises等效应力曲线，见图9、图10。

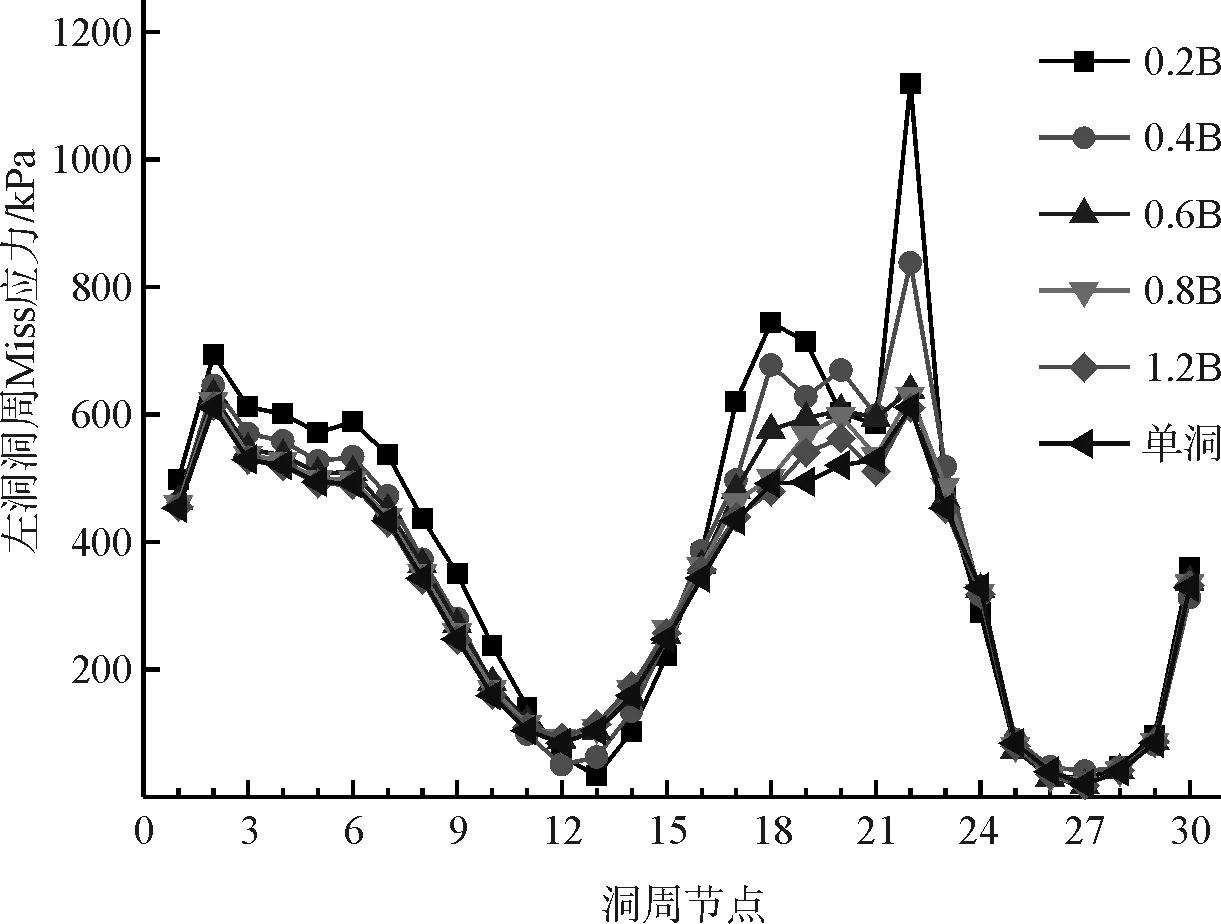
图9 不同净距下左洞洞周Mises应力

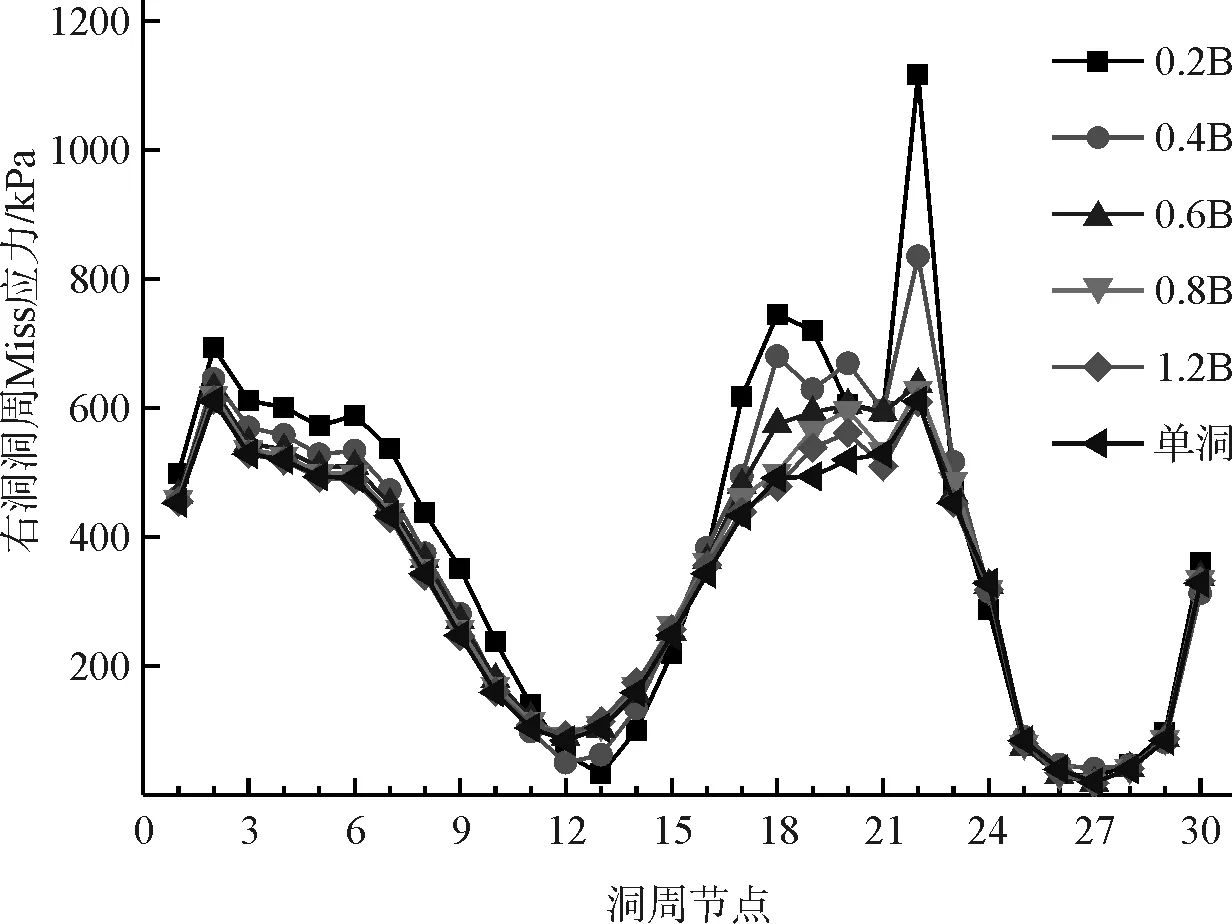
图10 不同净距下右洞洞周Mises等效应力

由图9、图10可知，左右洞洞周在同一测点处的Mises等效应力值相差不大，最大仅相差不到3 %；洞周Mises等效应力最大位置均发生在22号测点；净距改变对洞周Mises等效应力的影响范围主要集中在17～22号测点，其余各测点的Mises等效应力随净距的改变几乎不发生变化；净距从0.2B增加至0.6B的过程中，17～19号以及22号测点处的Mises等效应力迅速减小，当净距超过0.6B后，变化速率明显放缓，净距变化对上述测点Mises等效应力的影响已非常微小，且此时净距与单洞开挖的Mises等效应力曲线基本一致。

根据上述分析可知，当净距小于0.6B时，净距的改变主要影响夹岩附近的应力状态，且此时靠近拱脚处夹岩的Mises等效应力最大，是洞周最易出现屈服破坏的位置；当净距超过0.6B后，净距对洞周Mises等效应力的影响很小，可忽略不计。此外，发现20号、21号测点与净距无明显规律，这可能是净距改变过程中夹岩附近应力重分布的结果。

4 结束语

本文依托济南玉函路隧道工程，采用数值模拟的研究方法，分别对不同净距条件下毛洞开挖后的地表沉降、洞周水平位移、洞周Mises等效应力的计算结果进行了对比分析，得到以下结论：

(1)对比地表沉降的计算结果可知，净距较小时，夹岩对称轴处的地表沉降最大，沉降曲线为单一沉降槽；净距继续增大超过0.6B后，地表最大沉降位置将变为隧道中心在地表的投影处，沉降曲线呈“双槽形”，同时地表最大沉降变化也趋于平缓。

(2)对比洞周水平位移的结果可知，净距对洞周水平位移的影响范围主要集中在夹岩中部附近，净距较小时，水平位移随净距的变化非常敏感；净距增加超过0.6B后，洞周水平位移将几乎不受净距的影响。

(3)对比洞周Mises等效应力的结果可知，净距的改变主要影响夹岩附近的应力状态，拱脚附近的夹岩的Mises等效应力最大，是洞周最易出现屈服破坏的位置；净距超过0.6B后，净距对洞周Mises等效应力的影响很小，可忽略不计。

(4)综合本文的分析结果，对于类似的城市浅埋小净距隧道，可将0.6倍隧道跨度作为合理净距的参考依据。