相控阵雷达宽带干扰秩估计与干扰抑制
2020-06-06安瑞雪王晓林陈舒文
安瑞雪, 王晓林, 陈舒文, 张 伟
(1.电子科技大学信息与通信工程学院, 四川成都 611731; 2.北京控制与电子技术研究所, 北京 100038;3.中国航空工业集团公司雷华电子技术研究所, 江苏无锡 214063)
0 引言
宽带相控阵雷达因拥有更高的信号增益、角度分辨率、波束指向可控制性以及自适应抗干扰能力而被广泛使用[1]。宽带干扰时,抑制窄带干扰所需的自由度已经无法抑制宽带干扰,因此需要增加自由度。空时自适应干扰抑制是宽带波束形成的一个重要方法,克服了纯空域干扰抑制的缺点[2],大大增加了自由度。
杂波秩的估计对于空时自适应算法至关重要,文献[3-5]都探讨了杂波秩估计的方法,Klemm最早提出杂波子空间的秩约为N+L(N表示阵元个数,L表示脉冲数,也即时间采样数)。文献[6]研究了窄带干扰的秩估计但是并没有研究宽带干扰时的杂波秩估计的量化问题。
本文将量化分析宽带干扰的秩,利用宽带干扰信号的角度与频率之间存在的等效转换机制,然后采用椭球波函数可分解的正交函数的个数[7]来推导单宽带干扰时的秩,推广至两个及以上的多宽带干扰的秩估计。同时将研究宽带干扰秩和空时自由度之间的关系对分子阵宽带波束抗干扰性能的影响,干扰秩估计理论可作为设计自适应空时干扰结构的约束条件,在不失抗干扰性能的同时降低系统自由度的冗余。
1 相控阵干扰信号模型
若相控阵发射窄带信号,信号的带宽远小于载波频率,即B≪f0,对于阵元数为M的一个均匀线阵,其接收的窄带干扰回波信号的复基带离散信号表达式为
x(n)=a(θ)sp(n)+v(n)
(1)
式中:n表示快拍时间采样;sp(n)为参考阵元接收的干扰复信号;a(θ)=[1 ej2πf0dsinθ/c… ej2πf0(M-1)dsinθ/c]T∈CM×1为阵列的导向矢量,与干扰信号的载波频率f0、阵元间距d以及干扰信号入射角θ有关;c为光速;v(n)为噪声信号向量,且v(n)=[v0(n) …vM-1(n)]T∈CM×1。干扰回波信号的协方差矩阵为
(2)
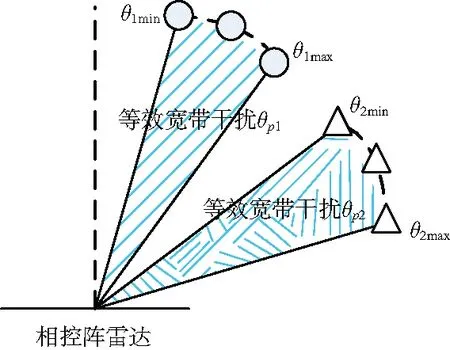
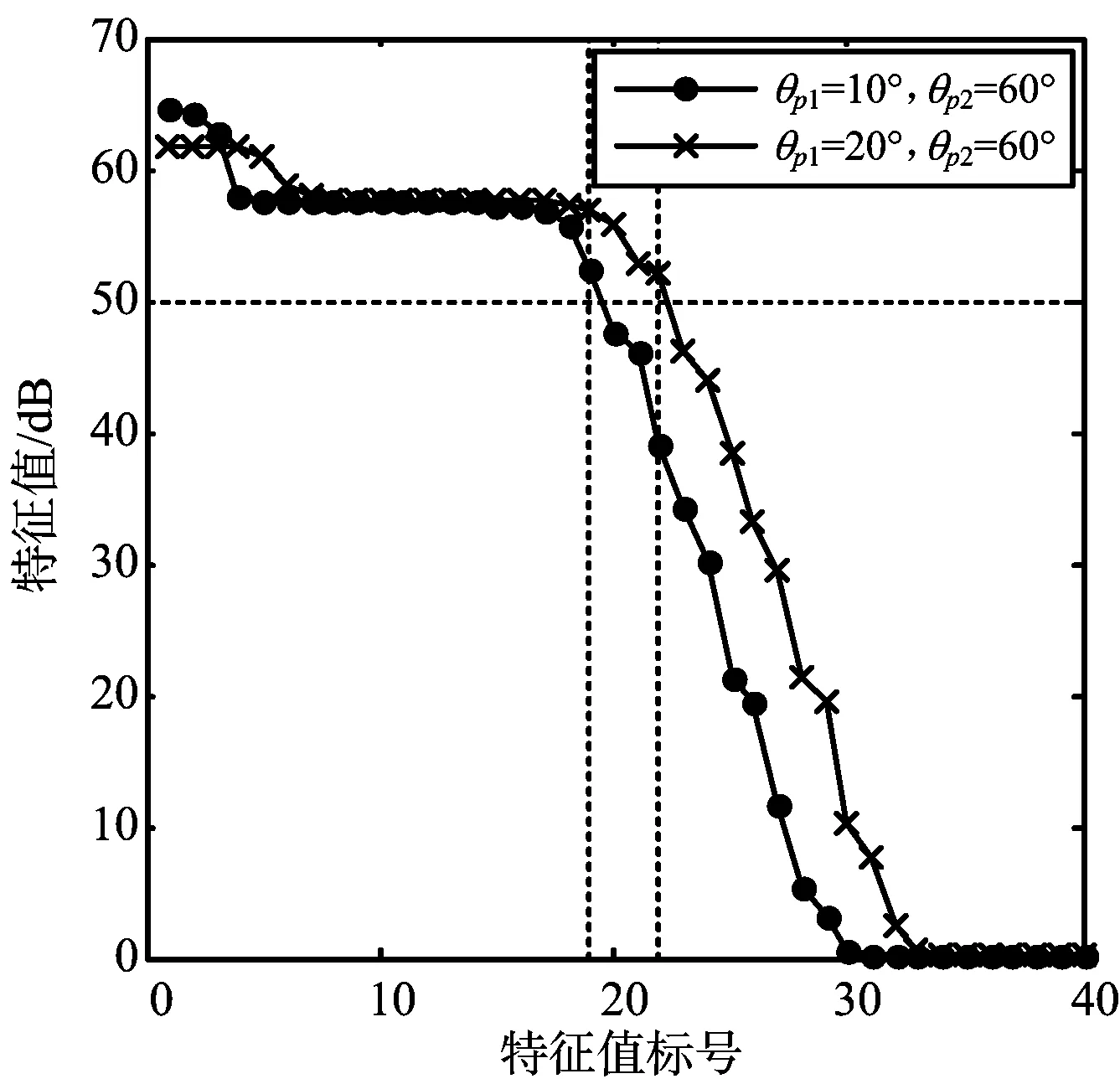
若有K(K x(n)=a(θ1)sp1(n)+a(θ2)sp2(n)+…+ a(θK)spK(n)+v(n) (3) 设sp(n)=[sp1(n)sp2(n) …spK(n)]T∈CK×1,A=[a(θ1)a(θ2) …a(θK)]∈CM×K,则可以写成矩阵形式: x(n)=Asp(n)+v(n) (4) 则K(K 宽带干扰信号不满足B≪f0这个条件,信号频率f∈[f0-B/2,f0+B/2],不能用载波频率f0来近似表示,故导向矢量与干扰角度θ和频率有关,表示为 a(θ,f)=[1 ej2πfdsinθ/c… ej2πf(M-1)dsinθ/c]T (5) 宽带干扰信号导向矢量张成的子空间的维度不为1,其自由度会随着带宽的增加而增加,所以常采用宽带波束形成算法来抑制宽带干扰信号,即通过空时处理的Frost结构[8]来增加时间自由度以抑制干扰。 Frost结构的核心思想是在每一个阵元后增加时域抽头以补偿因频率变化形成的相位差,在实际相控阵雷达系统中,为了达到波束主瓣宽度、信噪比和实时处理等需求,通常采用划分子阵的方式来降低系统的复杂度和自适应算法的维度。 分子阵的空时自适应波束形成器结构如图1所示,设总阵元数为M,阵元均匀划分且子阵间互不重叠。每个子阵均有J个阵元,一般M的值是J的整数倍,则一共有L=M/J个子阵。每个子阵内根据波束指向确定固定权值w0,… ,wJ-1,进行固定波束合成,子阵间则进行Frost空时自适应波束合成,即在每个子阵后均连接一个长度为N的抽头延迟线,共有LN个自适应权值{wl,n},l∈[0 1 …L-1],n∈[0 1 …N-1]。自适应权值可通过线性约束最小方差准则(LCMV)或者最小方差无失真响应准则(MVDR)求取。 图1 分子阵空时自适应波束形成器 单宽带干扰时,设带宽内的任一频率为f1∈[f0-B/2,f0+B/2],干扰信号入射角度为θp∈[0,π/2),为简化研究,进行如下等价转换: (6) 带宽内的任一频率f1变换为载波频率f0的过程中,与之对应的干扰角度需从θp等效为θ1,它们之间的关系为 (7) 若将带宽内的全部频率f都统一变换成载波频率f0,则有 (8) 式中,fmin=f0-B/2,fmax=f0+B/2。 如图2所示,转换之后的单宽带干扰信号可以看作由频率为f0,干扰角度范围为θ∈[θmin,θmax]的单频信号所构成,此为宽带干扰信号频率与角度之间存在的转换机制。 文献[7]提出如式(9)表示的椭球波函数: (9) 在时宽带宽积为一定值的情况下,该椭球波函数可表达为「2WT+1⎤个正交函数的线性组合。其中,W代表的是单边信号的带宽,「·⎤代表的是向上取整函数。 图2 单宽带干扰频率与角度等效转换机制 导向矢量亦可看成是椭球波函数,即把式(6)导向矢量中的变量m∈[0,M-1]看作式(9)中椭球波函数的变量t,因此式(9)中的T=M-1。将整体dsinθ1f0/c看成是式(9)中的f。其中θ1为转换之后的角度范围,不妨设为θmin≤θ1≤θmax,所以等效带宽为 (10) 干扰角度范围为θp∈(-π/2,0]时,进行同样的推导过程可得W=-dsinθpB/2λ0f0。所以综上,干扰角度为θp∈(-π/2,π/2)时,等效带宽为 (11) 通常情况下d=λ0/2,得到单宽带干扰信号的干扰秩表达式为 (12) 从式(12)可以看出,阵列的阵元数M、宽带干扰信号的干扰角度θp和带宽载波频率之比B/f0都会影响干扰的秩。反观窄带干扰的秩,因为B≪f0,故B/f0≈0,代入式(12),得到单个窄带干扰信号的秩是1,这与之前的结论是相吻合的。 在图2所示的等效转换机制基础上,根据这两个干扰信号等效变换后的干扰角度是否重叠分为两种情况:情况1 等效宽带干扰不重叠;情况2 等效宽带干扰重叠。 两个入射角为θp1和θp2转换后的等效宽带干扰如图3所示。若干扰角度θp1正负不同号于干扰角度θp2,此时两个等效干扰角度范围一定不存在重叠区间,为情况1。若干扰角度θp1同号于θp2,设0<|θp1|<|θp2|<π/2,则又有不重叠和重叠两种可能,若|θ2min|>|θ1max|,为情况1,如图3(a)所示;若|θ2min|<|θ1max|,则两个干扰角度区间相互重叠,为情况2,如图3(b)所示。而且sinθ2min=sinθp2fmin/f0,sinθ1max=sinθp1fmax/f0。综上可得如下定理: 定理一 两个等效干扰角度范围有重复区间的充分必要条件为宽带干扰角度θp1同号于θp2且假设|θp1|≤|θp2|时,一定有 (13) (a) 等效宽带干扰不重叠 (b) 等效宽带干扰重叠 若两个宽带干扰信号角度不重叠且其等效干扰范围为[θ1min,θ1max]∪[θ2min,θ2max],则由式(9)和式(10)可得等效带宽W为 (14) 若两个等效干扰角度存在重叠区间,等效变化区间为[θ1min,θ2max],此时等效带宽W为 (15) 若θp1和θp2符合定理一中的充分必要条件,那么干扰秩表达式为 (16) 若θp1和θp2不符合定理一中的充分必要条件,则两个单宽带干扰秩的和为其干扰秩: (17) 以此类推可得,存在多个宽带干扰N(N≥2)时,利用图3中的等效转化机制将N个宽带干扰等效转换,求取等效干扰角度的并集,得到等效带宽,最后利用式(12)计算出多干扰情况下的干扰秩。 本文共分为两组仿真实验,分别是仿真实验一:单宽带干扰信号干扰秩仿真实验和仿真实验二:两个宽带干扰信号的干扰秩仿真实验。仿真时,宽带干扰信号均选取宽带噪声干扰,设置干噪比JNR=50 dB,在图中纵坐标数值为50 dB的地方标出一条点线,因为协方差矩阵秩本质上是协方差矩阵主要特征值数目,故大于等于50 dB的特征值则被认为是宽带干扰信号的主要特征值。 仿真实验一:单宽带干扰信号干扰秩估计实验。干扰秩估计表达式(12)表明干扰秩与三种因素相关,因此需控制单一变量。其中影响因素B/f0为两个参数,为实现不同的带宽载波频率比值,保持信号带宽不改变,改变载频大小。如图4中的(a)、(b)、(c)依次为3个不同变量干扰角度θp、阵元数M和带宽载波频率比值B/f0的特征谱仿真图。 1) 不同干扰角度的特征谱仿真 仿真条件与结果分析:阵元数M=80、信号带宽B=400 MHz、载频f0=1 GHz,干扰角度θp取值为10°,30°,50°和80°。通过计算式(12)得到此仿真情况下的理论值,分别为4,9,14和17。在图4(a)中用4条虚线标出最大特征值标号,结果可以看出这些干扰角度分别对应的最大特征值标号为4,9,14和16,与推导的理论估计值基本一致。 2) 不同阵元数的特征谱仿真 仿真条件与结果分析:干扰角度为50°,信号带宽B=400 MHz,载频f0=1 GHz。阵元数取值分别为40,80,120和160,依据式(12)计算此仿真条件的估计值,干扰秩理论估计值为7,14,20和26,在图4(b)中同样用4条虚线标出最大特征值的标号,结果可以看出这些阵元数分别对应的最大特征值标号为7,14,20和26,与理论推导干扰秩估计结果也是吻合的。 3) 不同载波频率的特征谱仿真 (a) 不同干扰角度的特征谱 (b) 不同干扰角度的特征谱 (c) 不同载波频率的特征谱 仿真条件与结果分析:干扰角度为50°,阵元数M=80,保持信号带宽不变B=400 MHz,改变载频f0,取值分别为1,1.5,2和2.5 GHz,依据式(12)计算此仿真条件的估计值,分别为14,10,8和6。从图4(c)仿真结果可以看出这些不同载频分别对应的大于等于50 dB的最大特征值标号分别为14,10,8和6,亦与理论推导结果相吻合。 根据以上3个仿真条件下的结果,进一步证实了单个宽带干扰信号干扰秩估计表达式(12)的正确性。 仿真实验二:相互独立的两个宽带干扰信号干扰秩估计实验。在实验中根据等效宽带重叠与否,设置两类仿真条件来验证式(16)和式(17)中干扰秩估计的结果。阵元数M=80,信号带宽B=400 MHz,载频f0=1 GHz,所以fmax/fmin=1.5,保持两个干扰信号中较大的干扰角度不变,为θp2=60°。 从定理一易知,当sinθp1>35.3°时等效转换干扰角度重叠,当sinθp1<35.3°时不重叠。故等效宽带不重叠时选择θp1为10°和20°,不同的θp1的仿真结果如图5(a)所示;等效宽带重叠时,选择θp1分别为40°和50°,结果如图5(b)所示。 (a) 干扰等效宽带不重叠 (b) 干扰等效宽带重叠 等效角度干扰范围不重叠时,通过计算式(17)得到θp1=10°时干扰秩估计理论结果为19,θp1=20°时干扰秩估计理论结果为22,图5(a)的仿真结果可以看出θp1=10°时功率大于50 dB的最大特征值标号为19,θp1=20°时功率高于50 dB的最大特征值标号为22,与式(17)估计计算结果相吻合。 等效角度干扰范围重叠时,通过式(16)可计算得到θp1=40°时干扰秩理论估计值为22,θp1=50°时干扰秩理论估计值为18,图5(b)的仿真实验结果也可以看出θp1=40°时,功率大于50 dB的最大特征值标号为22,θp1=50°功率大于50 dB的最大特征值标号为18。 进一步观察分析图5(a)的仿真结果可知,θp1从10°增加至20°时,此时θp1依然未与θp2重叠,故秩随着干扰角度θp1的增加而增大,所以干扰秩从19增加至22;但是当sinθp1>35.3°时,等效宽带干扰便出现重叠区域,θp1越大,重叠区域会越大,秩会相应减小。在θp1从40°增加至50°时,干扰秩会从22减小至18。亦说明了理论推导的准确,等效宽带干扰并集之秩即两个宽带干扰信号的干扰秩。 设计图1的分子阵空时自适应波束形成器时,通常需要设计子阵个数L和抽头延迟线阶数N,则LN即为系统的空时自由度。分子阵空时波束形成器的抗干扰性能随着子阵数和抽头延迟线阶数的增加而提高[8]。在有限的硬件资源和实时性要求的限制条件下,不允许L和N无限度地增加。现通过研究宽带干扰秩和空时自由度之间的关系对分子阵宽带波束抗干扰性能的影响,将宽带干扰秩估计应用于L和N的设计中。 用抗干扰前后的干扰功率的比值,即对消比来作为干扰抑制的性能指标。对消比的定义如下: (18) 式中,Pjb表示抗干扰之前系统的干扰功率,Pja表示抗干扰之后系统的剩余干扰功率。 由定义可知,对消比总是非负的,且对消比越大,抗干扰能力越强,当对消比越接近时抗干扰能力越弱,且当对消比为0时,系统没有抗干扰的能力。仿真条件如下,阵元数M=120,每个子阵内阵元数J=12,一共有10个子阵,期望信号角度为0°,信噪比为0 dB,信号带宽B=400 MHz,载波频率f0=1 GHz,单个宽带噪声干扰,干扰信号带宽也为400 MHz,干噪比为50 dB。由式(12)可知,当干扰角度从0°变化到90°时,干扰秩从1增加到25,且当干扰角度为20°时,干扰秩增加到10,当干扰角度为50°时,干扰秩增加到20。 在图6中,仿真了时延抽头阶数N=1,2,3,4情况下的干扰对消比与干扰角度之间的关系。 图6 不同抽头延迟线阶数抗干扰性能与干扰角度的关系(10子阵) 当N=1时,等效于纯空域的波束形成,系统只有10个空域自由度,因此从图6中的虚线可知,当干扰角度为20°时,干扰秩增加到10,加上约束期望信号所需的一个自由度,已经超过系统的10个空域自由度,对消比急剧下降且靠近0 dB。所以在纯空域结构下在20°附近出现拐点,当超过20°时,干扰秩已经大于系统自由度,无足够自由度去抑制干扰,抗干扰性能急剧下降。 当N=2时,即每个子阵后均有一个延迟抽头,系统的空时自由度为20,从图6中的点线可知,当干扰角度为50°时,干扰秩增加到20,加上期望信号的一个自由度,超过了系统的20个空时自由度,对消比急剧下降至3 dB附近。在N=2时,对消比性能在50°附近出现拐点,当超过50°时,干扰秩大于系统的空时自由度,同样无足够自由度去抑制干扰,抗干扰性能急剧下降。 当N=3时,即图6中的实线,此时的系统空时自由度为30,由于单个宽带干扰秩在该条件下的最大值为25,因而系统有足够的自由度去抑制单个宽带干扰,系统干扰对消比不会出现性能急剧下降的拐点,且对消比稳定在30 dB以上。同理,当N=4时,即图中的虚点线,同样有足够的自由度去抑制该条件下的单个宽带干扰,因而对消比也稳定在30 dB以上。 综上所述,图6中的仿真结果在验证式(12)的单宽带干扰秩估计公式的同时,研究了干扰秩与系统自由度之间的关系对抗干扰性能的影响。其结论如下:当干扰秩大于系统自由度时,系统无足够的自由度来抑制宽带干扰,抗干扰性能急剧恶化,在空时结构中,可以通过增加时延抽头阶数N来增加空时自由度。当空时自由度大于当前条件干扰秩的最大值时,再增加抽头阶数N,对抗干扰性能改善已很小。通过以上结论,可以用来作为设计分子阵阵列的子阵个数L和抽头延迟线阶数N的一个约束条件,即先通过干扰秩公式估计该条件下的最大干扰秩,在满足LN大于最大干扰秩时,使L和N尽可能小。 本文通过一种角度与频率之间等效转换机制来转换宽带干扰信号,通过椭球波函数可分解的正交函数的个数,类推出宽带相控阵雷达中单个与两个宽带干扰秩估计的量化表达式。干扰角度、阵元数和带宽载波频率比值这三个因素影响单宽带干扰的秩。两个宽带干扰时,通过等效转换之后的等效干扰区间重叠与否,给出两种情况下的秩估计的推导,并给出判定两个等效转换后的宽带干扰区间是否重叠的充分必要条件。同时两个宽带干扰秩估计的思想可以引申推广到多宽带干扰时的干扰秩估计。本文通过仿真实验,证实了干扰秩估计表达式的准确性。通过宽带相控阵雷达中的宽带干扰秩估计,量化了宽带干扰抑制所需的自由度,研究了宽带干扰秩和空时自由度之间的关系对抗干扰性能的影响,可将此理论应用于分子阵宽带波束形成器的子阵数和抽头延迟线阶数的设计中。今后可在此基础上,对最优降维自适应波束形成器作进一步的研究。2 分子阵空时自适应波束形成器

3 宽带相控阵干扰秩估计
3.1 单宽带干扰秩估计



3.2 多宽带干扰秩估计



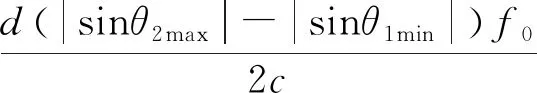

4 干扰秩估计仿真实验及其在子阵波束形成器的影响和应用
4.1 宽带相控阵干扰秩估计仿真实验




4.2 宽带干扰秩对抗干扰性能的影响及应用

5 结束语
