一类分数阶地磁系统的动力学行为研究

高忠社

（天水师范学院 数学与统计学院，甘肃 天水 741000）

分数阶微积分作为数学学科的一个重要分支，是传统整数阶微积分的推广和发展，近些年来，分数阶微积分引起了很多科学领域学者的关注和研究，分数阶微积分在描述反常扩散、粘弹性力学、流体力学、管道的边界层效应、电磁波、量子经济、分形理论等领域都有很重要的应用.另外，分数阶系统是描述很多自然现象的重要工具，很多学者提出了许多不同的分数阶系统.[1,2]

混沌是非线性动力系统在一定条件下表现出的一种运动形式，是确定性系统中出现的随机现象.分数阶系统是描述很多自然现象的有效工具.很多学者提出了不同的分数阶混沌系统，并且研究了它们的动力学行为.不同领域的学者对分数阶混沌系统的动力学行为作了广泛的研究并得到了非常重要的成果.本文将在文献[3]的基础上，研究地磁系统丰富的动力学行为.

1 预备知识

分数阶微分算子

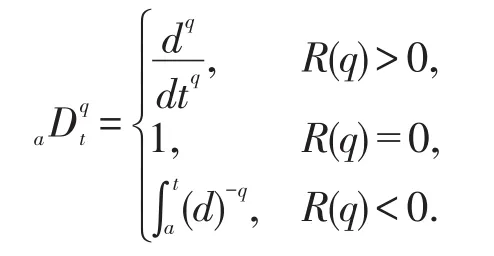
上式中，q表示分数阶，R(q)表示q的实部，实数a和t分别表示积分的上、下限.Riemann-Liouville导数和Caputo导数是目前常用的分数阶微积分的定义.

Riemann-Liouville（RL）积分算子[3]设 Γ(q)是伽玛函数，其中q＞0，定义于Lebesque空间L1[t0,t1]算子

称该算子为q阶Riemann-Liouville（RL）积分算子，.

Riemann-Liouville（RL）导数算子[3]设 Γ(q)是伽玛函数，其中q＞0且m∈N，使得m-1＜q＜m，定义于Lebesque空间L1[t0,t1]积分算子

当t0＜q＜t1时，称该算子为q阶Riemann-Liou-ville（RL）导数算子..

当t∈L1[t0,t1],q≥0,γ＞-1时有性质：

Gorenflo,R.&Mainardi,F.等人发现Riemann-Liouville（RL）导数算子使用时的诸多不便，Capu⁃to对于上述算子作了做一步的修改，得到

Caputo导数算子定义[4]

对于t∈L1[t0,t1],m∈N，使得m-1＜q＜m，t＞0，则有

其中0＜α＜1的实数，Γ(·)表示伽玛函数

对于分数阶非线性系统的数值求解，使用K.Diethelm，等人提出的预估-校正法，考虑如下方程

根据文献[6,7]可知，方程组（1）等价于下列Volterra积分方程

2 模型及分数阶系统稳定性分析

引理[5]对于分数阶系统

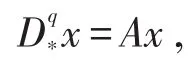
渐近稳定的充分条件是矩阵A的特征值满足如下条件

在文献[3]中，D.R.J.Chillingworth and P.J.H-olmes等，提出了一个整数阶混沌系统，方程组如下

文中分析了参数a,R,v在不同值时，在三个平衡点的不同的稳定性分析；研究了在参数R,v固定的情形下，对于参数a的分岔行为，以及研究了Hopf分岔的Lyapunov系数一阶导数.本文将在文献[3]基础上研究分数阶导数对于该系统平衡点的稳定性，及对于参数a,R,v的分岔行为，及系统阶数q的分岔情况.文中的分数阶导数使用Caputo导数，数值求解方法使用Diethelm K.等人提出的预估校正法.

是系统渐近稳定的节点.对于P±(x,y,z)，系统对应的Jacobian矩阵为

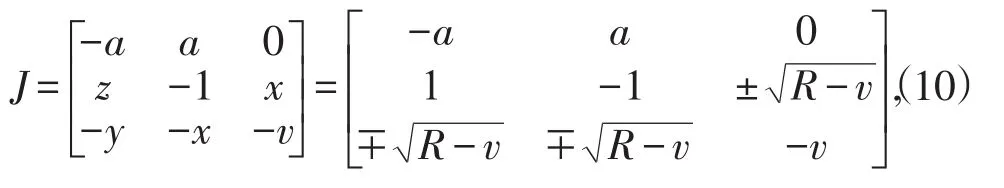
则Jacobian矩阵在R=18,a=5,v=1有相同的特征根

λ1=-7.12208;

λ2=0.0610385-4.88525i;

λ3=0.0610385+4.88525i;

其中λ1是一个负实数，且|arg(λ2,3)|=1.5593，分数阶系统（8）的阶数在0.992046≤q≤1.0范围时，该系统有两个不稳定的平衡点.

利用预估-校正法，对分数阶混沌系统（8）进行离散化处理，则有混沌系统的离散化形式为

其中αj,n+1，βj,n+1由（5）,（6）式可得，给定参数和初值，就可以得到分数阶微分方程的数值解.[6,7]

3 分数阶系统的混沌和分岔分析

文中使用文献[4,5]Diethelm K.等人提出的预估校正法fde12对系统（8）不同的参数进行仿真实验.为了研究系统（8）动力学行为，系统参数a作为分岔参数，固定系统其他系统参数和系统阶数，系统参数v=1，R=18，初值

x(0)=0.1,y(0)=0.1,z(0)=0.1，

系统阶数q=0.9981，分岔图如图1所示.

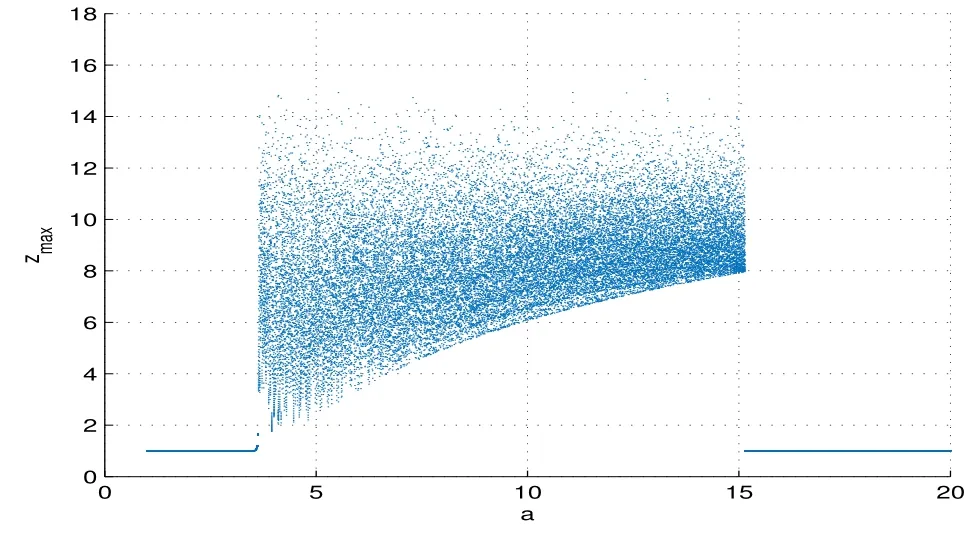
图1 当系统参数a∈(0,20)，分数阶系统（8）的分岔图

从图1观察发现，当参数a＜3.8时，系统（8）出现一系列的周期轨道，当a=3.8时，系统（8）发生了霍普夫分岔，进入混沌状态；当a＞14.5时，系统（8）从混沌状态进入了周期轨道.当对于系统不同的参数，对应不同的相图，如图2，3，4所示.

图2 当参数a=2，v=1，R=18时，系统的相图

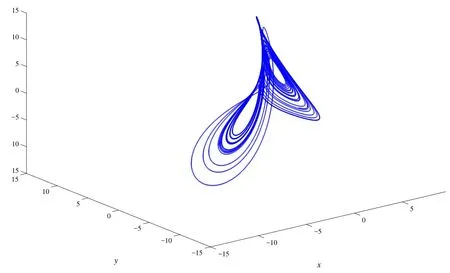
图3 当参数a=6，v=1，R=18时，系统的相图

图4 当参数a=18，v=1，R=18时，系统的相图

R作为分岔参数，固定系统参数v=1，a=6，系统初值

x(0)=0.1,y(0)=0.1,z(0)=0.1，

系统阶数q=0.9981，分岔图如图5所示.

图5 当系统参数R∈（0,35），分数阶系统（8）的分岔图

从图5观察发现，当参数R＜15.3时，系统（8）出现一系列的周期轨道，当R=15.3时，系统（8）发生了霍普夫分岔，进入混沌状态；当R＞15.3时，系统（8）从混沌状态进入了周期轨道.对于系统不同的参数.对应不同的相图，如图6，7，8所示.

图6 当参数a=6，v=1，R=10时，系统的相图

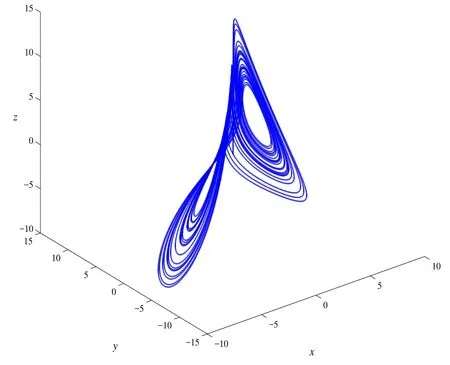
图7 当参数a=6，v=1，R=20时，系统的相图

图8 当参数a=6，v=1，R=22时，系统的相图

系统参数v作为分岔参数，固定系统参数R=18，a=6，给定初值

x(0)=0.1,y(0)=0.1,z(0)=0.1，

系统阶数q=0.9981，分岔图如图10所示.

图9 当系统参数v∈(0,2)，系统阶数（8）的分岔图

从图9观察发现，当参数v＜0.1时，系统（8）出现一系列的周期轨道，当v=0.1时，系统（8）发生了霍普夫分岔，进入混沌状态；当0.1＜v＜1.15时，系统（8）进入了混沌状态；当v=1.15时,系统（8）发生了霍普夫分岔；当v＞1.15时系统（8）从混沌状态进入了周期轨道.对于系统不同的参数，对应不同的相图，如图10，11，12所示.

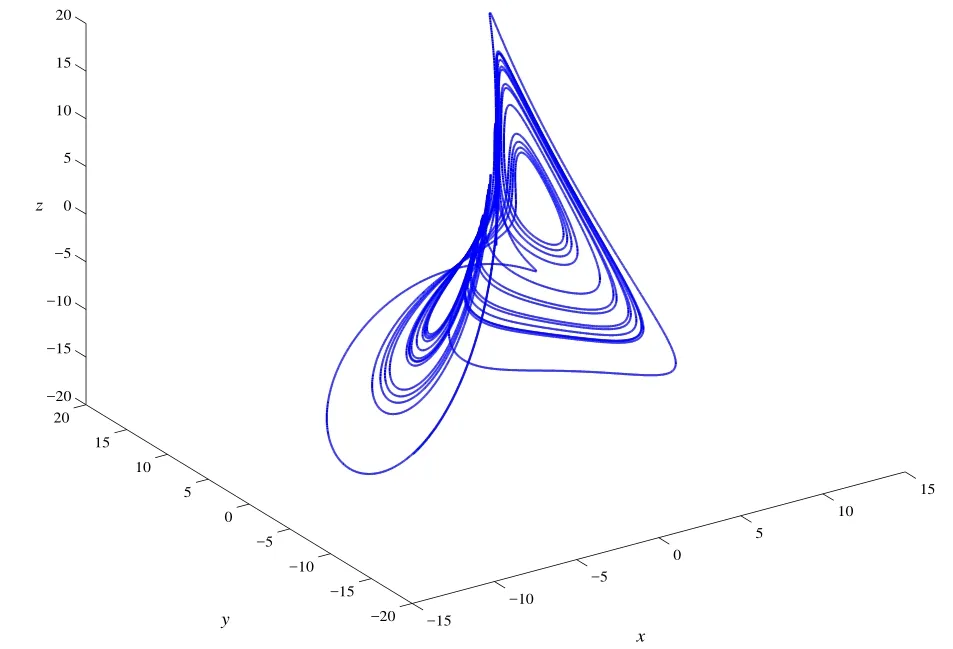
图10 当参数a=6，v=0.17，R=22时，系统的相图

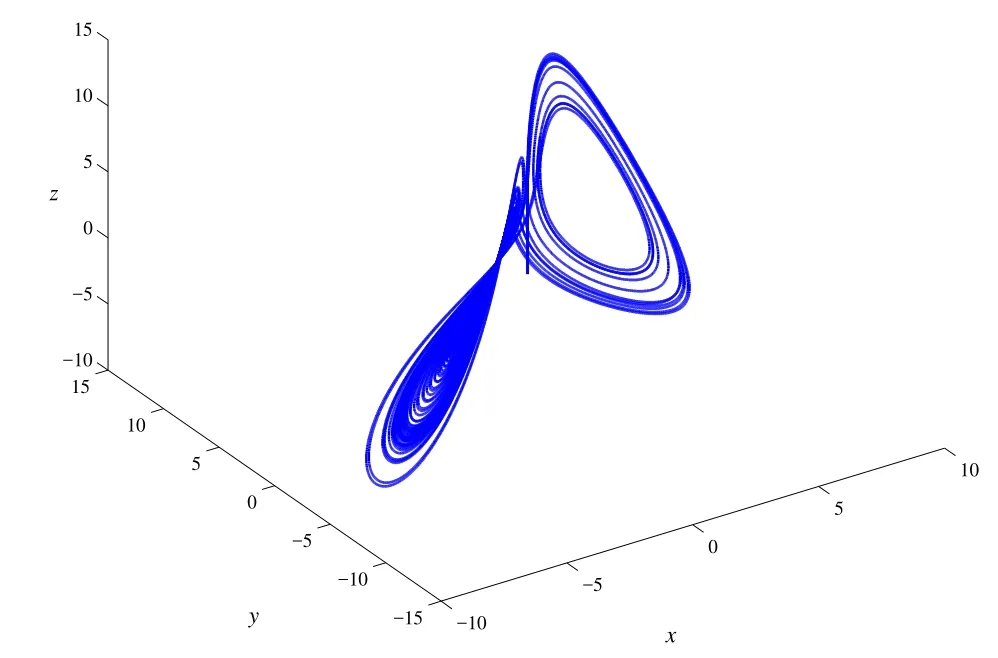
图11 当参数a=6，v=1.4，R=22时，系统的相图

图12 当参数a=6，v=1.8，R=22时，系统的相图

通过选取系统（8）不同的分岔参数，对系统（8）的动力学行为进行了详细研究，结果表明，系统的参数都对它的动力学行为产生很大的影响，系统对不同的参数，吸引子有很大的差异.

对于研究系统（8）丰富的动力学行为，系统阶数对动力学行为有重要的影响作用，系统阶数q作为分岔参数，固定系统其它系统参数，

R=18，a=6，v=1，

初值x(0)=0.1,y(0)=0.1,z(0)=0.1，分岔图如图13所示

图13 当系统参数a∈(0.984,1)时，系统(8)的分岔图

从图13观察发现，当参数q＜0.9925时，系统（2）出现一系列的周期轨道，当q=0.9925时，系统（8）发生了霍普夫分岔，进入混沌状态；当0.9925＜v＜1时，系统（8）进入了混沌状态；当对于系统不同的阶数，对应不同的相图，如图14，15，16所示.

图14 当阶数α=0.95时，系统的相图

图15 当阶数α=0.98时，系统的相图

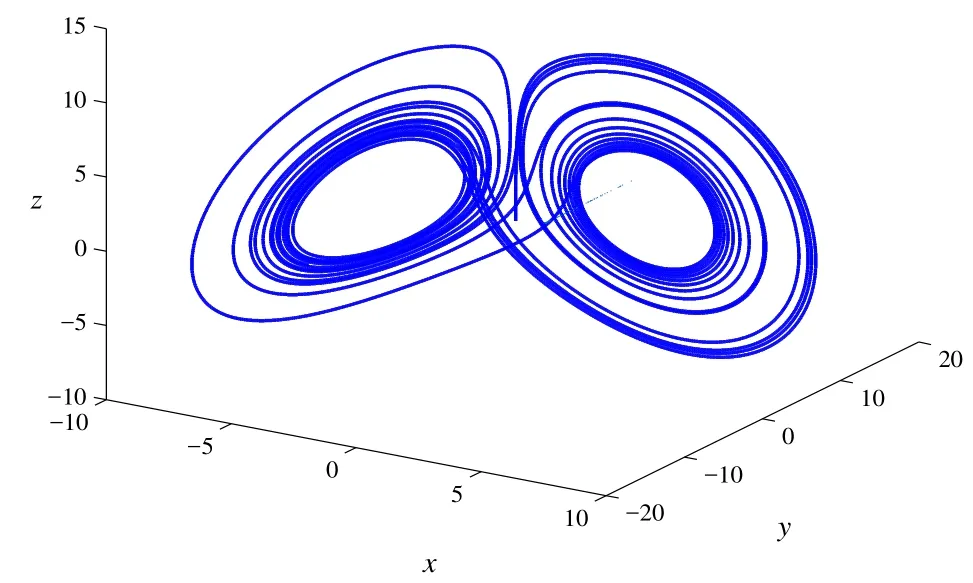
图16 当阶数α=0.99时，系统的相图

通过选取系统（8）不同的阶数，对系统（8）的动力学行为进行了详细分析，结果表明，系统的阶数都对它的动力学行为产生很大的影响，系统对不同的阶数，吸引子有很大的差异.

4 结语

本文研究了分数阶地磁系统动力学行为，首先，从理论上研究了该系统的一些基本特征，平衡点、特征值以及系统阶数.其次，使用预估-校正法，借助数学软件MATLAB进行数值仿真，通过对于系统每个参数分岔图分析研究，对于系统阶数和参数的调整，得到系统在不同条件下的吸引子以及分岔图.研究结果表明，分数阶新系统有不同的分岔行为，包括霍普夫分岔及鞍结分岔等形式，及该系统有丰富的动力学行为.