局部对称拟常曲率黎曼流形中的极小子流形

李明图，裴瑞昌

（天水师范学院 数学与统计学院，甘肃 天水 741001）

设Nn+p(c)是截面曲率为常数c的n+p维黎曼流形，Mn是等距浸入在Nn+p(c)中的n维紧致子流形，σ表示其第二基本形式模长的平方，若Nn+p(c)是球面，当Mn极小时，有著名的Simons型积分不等式[1]：

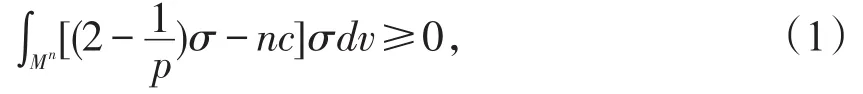
其中dv表示Mn上的体积元素.当p≥2时，李安民教授对 （1）式做了改进，得到了一个与余维数p无关的结果[2]：

白正国教授在文献[3]中对拟常曲率黎曼流形中的紧致极小子流形做了讨论.Ganchev G.和Mihova V.在文献[4]中将ξ理解为一个向量，进而考虑了拟常曲率黎曼流形的几何特征.之后，Bejian C.L.和Oproiu V.在文献[5]中从ξ是向量的角度研究了具有拟常全纯截面曲率的切丛.本文考虑了局部对称拟常曲率黎曼流形中的紧致极小子流形上的类似问题，分别在ξ∈Γ(TM)和ξ⊥Γ(TM)的情形下，得到了两个定理，推广了文献[2]中的结论.

1 准备工作

文中约定各指标的变程为：

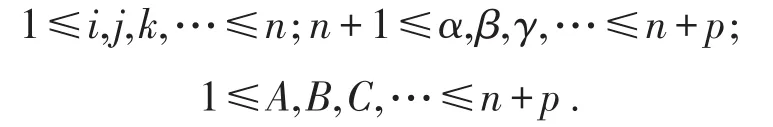
在Nn+p上选取标准正交标架场{e1,e2,…,en+p},使得限制在Mn上时，{e1,e2,…,en}与Mn相切，{en+1,en+2,…,en+p}垂直于Mn.设{ω1,ω2,…,ωp} 是其对偶标架场，则Mn的结构方程为

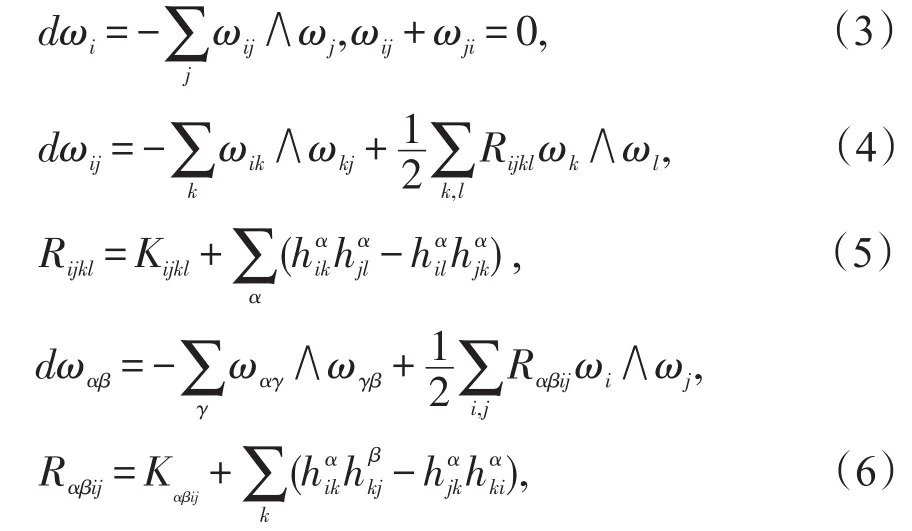
Rijkl和Rαβij分别表示Mn的黎曼曲率张量分量和法曲率张量分量.记,Hα的迹为,用h,H,σ分别表示Mn的第二基本形式，平均曲率和第二基本形式模长的平方，有

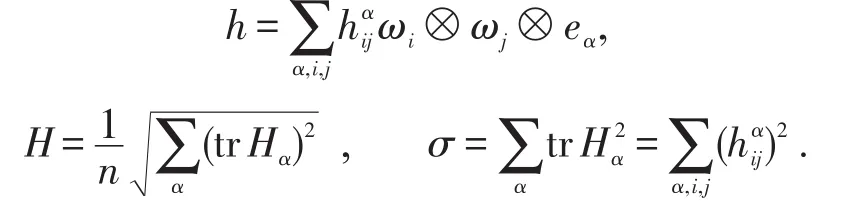
用hijk和hijkl分别表示的一阶及二阶协变导数，有

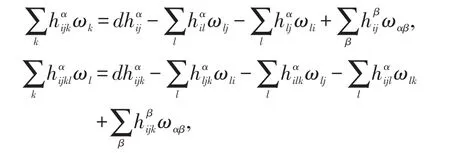
若Nn+p是局部对称的，由文献[6,7]可知：对于任意实常数λ，有

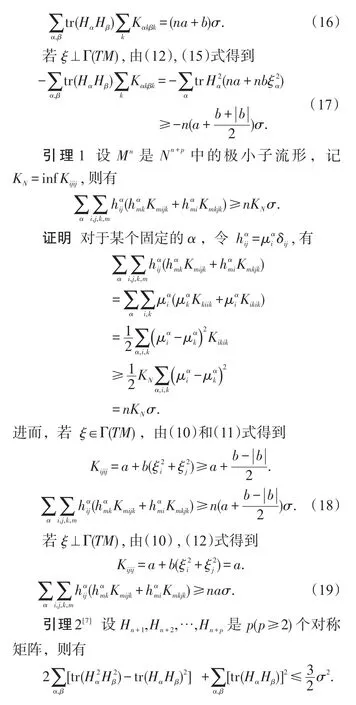
2 主要定理及其证明