一类具有年龄和病程的传染病模型的等价积分方程组
2020-06-05王天松
俞 芳,李 硕,王天松
(1.昌吉学院 数学系,新疆 昌吉 831100;2.陕西师范大学 数学与信息科学学院,陕西 西安 710119)
许多传染病的传播受年龄、病程因素的影响较大,如乙肝、艾滋病等传染病.早在20世纪80年代,李大潜在文献[1]和[2]中分别建立了同时具有年龄和病程的终身免疫型传染病模型和非终身免疫型传染病模型,从数学上将传染病的传播归结为对一类非线性双曲方程组定解问题的研究.姚勇[3]利用Banach不动点定理得到了文献[1]中的传染病模型解的适定性.除了年龄和病程因素,潜伏期也是影响传染病传播的一个重要因素,闫萍在文献[4]中利用Banach不动点定理和先验估计方法证明了一类具有潜伏期、病程和年龄的无免疫型传染病模型解的适定性,并讨论了解的正则性.对于终身免疫型的传染病,由守科和闫萍[5]证明了具有年龄、病程和潜伏期因素的SEIR传染病模型的解的适定性.俞芳和由守科等[6]对文献[5]中的SEIR模型进一步讨论,证明了无病平衡解的全局渐近吸引性.由于同时考虑年龄、病程、潜伏期因素的传染病模型结构较为复杂、研究难度较大,所以研究结果较少.
闫萍和吴昭英在文献[7]将人群分为了易感类人群和染病类人群,考虑了自然年龄、病程因素、因病死亡率和免疫性因素对疾病的影响,建立了具有年龄和病程结构的非自治传染病模型,来描述一类具有无免疫性和致命性特点的传染病.鉴于模型结构极为复杂,并没有讨论模型解的相关性质.本文主要针对无因病死亡并且出生率、感染率、治愈率仅依赖于年龄的无免疫型传染病进行研究,因此在文献[7]的模型中令因病死亡率等于零,不考虑时间和病程因素对出生率、自然死亡率、感染率、治愈率的影响,并且假设两类人群的自然死亡率相等,得到无免疫型传染病模型
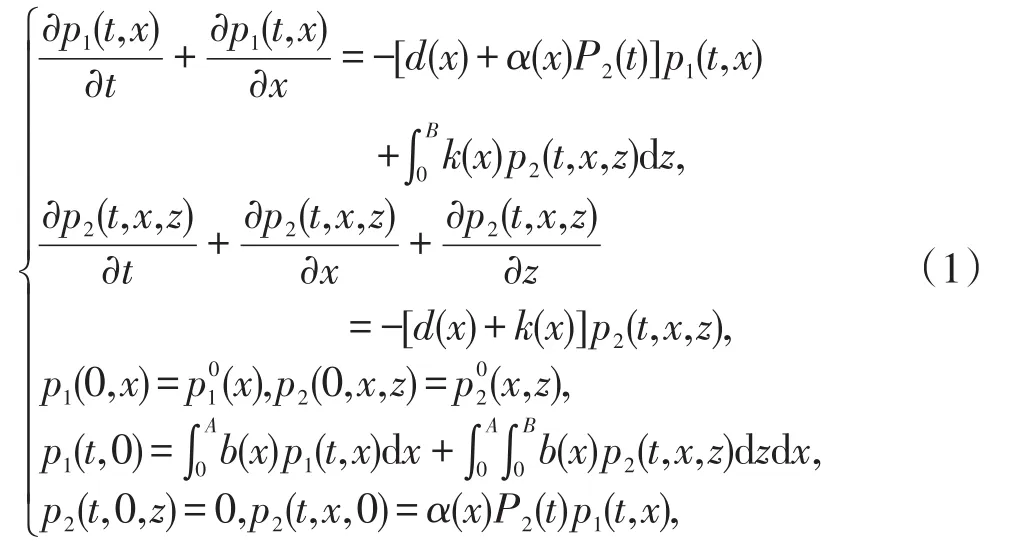
其中p1(t,x)和p2(t,x,z)分别表示易感类人群密度分布和染病类人群密度分布,变量t,x,z分别是时间、自然年龄、病程;A和B表示自然年龄上限和病程上限;根据病程不可能超过年龄的事实,当z>x时,p2(t,x,z)=0;非负连续可微函数b(x),d(x),α(x),k(x)表示出生率、自然死亡率、感染率、治愈率;
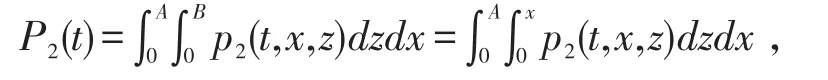
表示t时刻染病类人数.
对模型(1),由姚勇[3]的思想,利用不动点定理,证明模型(1)非负解的存在性.本文将主要利用偏微分方程的特征理论,研究模型(1)平衡解满足的积分方程.
1 模型转换
由模型(1)可知,总人口密度分布为
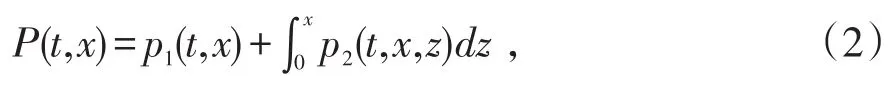

2 平衡解满足的积分方程组


