新五模类Lorenz系统的动力学行为分析及仿真

王贺元, 李 佳, 王美玉, 宋斯琦, 王晓帆, 曹婷婷

(沈阳师范大学 数学与系统科学学院, 沈阳 110034)

0 引 言

刻画流体运动的Navier-Stokes方程是经典的非线性偏微分方程,研究其解的性态有助于认识湍流的生成机理。探讨其解的稳定性及分岔问题是近些年人们普遍关注的焦点,吸引众多学者对其进行了广泛的研究。自混沌之父Lorenz[9]给出著名的Lorenz系统以来,采用降维方法讨论无穷维动力系统方面的工作层出不穷[1-8]。Valter Francechini科研团队将如下的Navier-Stokes方程

其中:u为速度场;f为外力;p为流体压强;ν为动力粘性系数。

在平面规则区域上进行有限维约化,获得了一些有限维的动力系统[1-4]。基于二维区域上的这种约化方法,Franceschini等[7]讨论了三维区域上的Navier-Stokes方程,获得了空间区域上的五模系统,后来又陆续得到了七模、十四模等有限维动力系统,并且探讨了这些有限维系统复杂的动力学性态[3]。

本文将约化二维区域上不可压缩Navier-Stokes方程,获得新五维类Lorenz系统,探讨系统吸引子的存在性,并进行全局稳定性分析,对系统动力学行为进行数值仿真。

1 Navier-Stokes方程的约化及类Lorenz系统的稳定性

对平面区域[0,2π]×[0,2π]上Navier-Stokes方程进行有限维约化,把速度场u,外力f,压强p展开为如下傅氏级数:

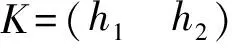
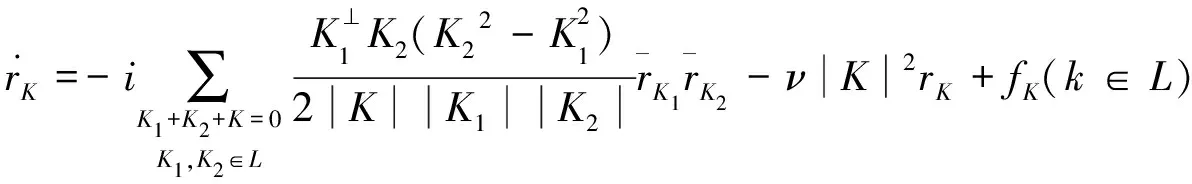
其中:ν为动力黏度系数;L为波向量集合,并且有若K∈L则-K∈L。

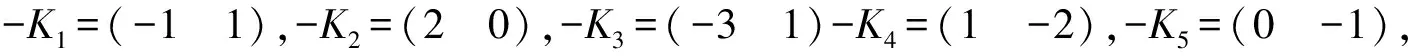
在ν=1时分别令K为K1,K2,K3,K4,K5,代入到方程组(7)经大量计算,得到如下方程组:

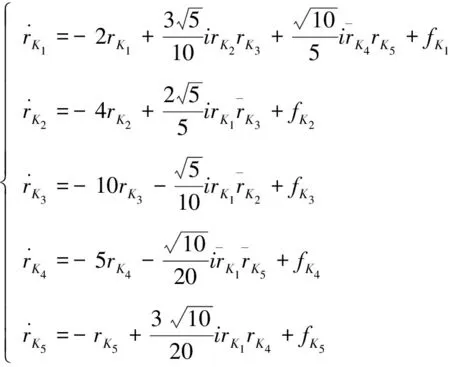
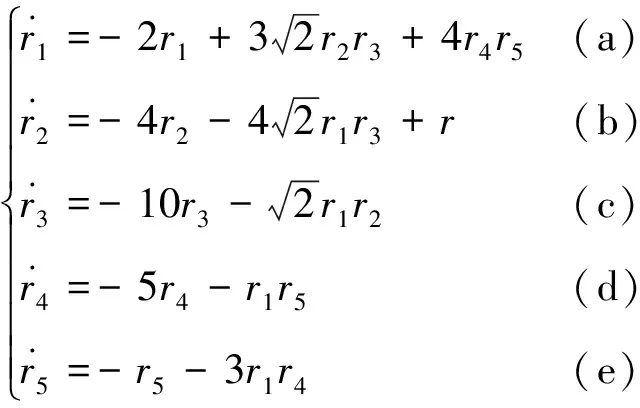
基于奇点邻域内的线性稳定性分析可以讨论非线性系统解的性态,这就是Liapunov第一方法[5]。Liapunov矩阵的特征指数是指Jacobi矩阵特征值的实部,它能较好地刻画吸引子的性质。基于奇点的Liapunov矩阵的特征指数可以分析和讨论奇点的稳定性。

令

对F(X,r)求导数得到

由F(X,r)=0求出奇点,依据Liapunov矩阵的特征指数符号判别各奇点的稳定性:

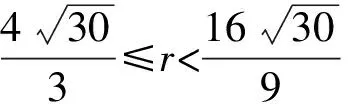
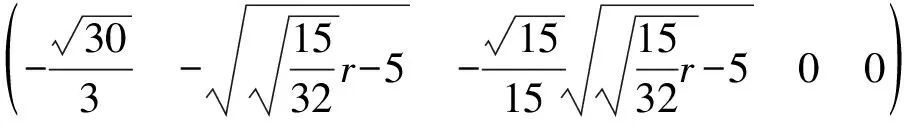
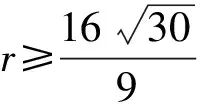
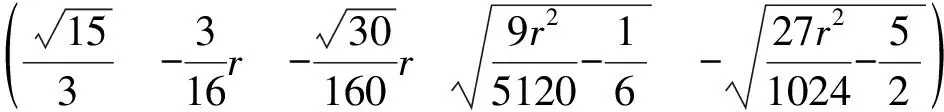
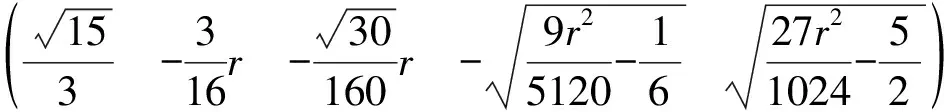
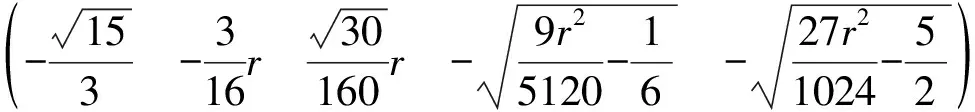
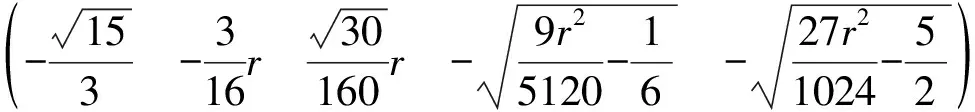
对于奇点(1)(2)(3),由于Jacobi矩阵特征值的变化而失去稳定性,奇点(4)(5)(6)(7)在r<9.737…的范围内始终是稳定的。

2 吸引子的存在性

非线性方程解的性态是极其复杂的,一般无法通过简单的推导和运算来获得。近年来,基于Sniale等的思想[8],耗散系统的混沌行为是由于存在混沌吸引子引起的,而混沌吸引子是系统所有轨道的长时间行为。混沌吸引子的复杂结构是导致系统出现混沌现象的原因。所以,探讨吸引子的存在性就显得尤为重要。下面讨论系统(9)吸引子的存在性。

对系统(9)进行运算

(a)×r1+(b)×r2+(c)×r3+(d)×r4+(e)×r5得:

因此有

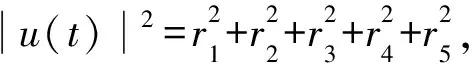
取ε=2,得

因此有

故有

当ρ充分大时,B(0,ρ)是吸引集和泛函不变集,因此存在全局吸引子。

3 全局稳定性

如果具有全局稳定性,系统的轨线所收敛的单连通闭区域称为系统的捕捉区。如果能证明捕捉区存在,也就表明无论奇点是否稳定,系统永远是全局稳定的。基于Liapunov第二方法[5],构造V函数讨论系统(9)的稳定性。

对系统(9)构造Liapunov函数:

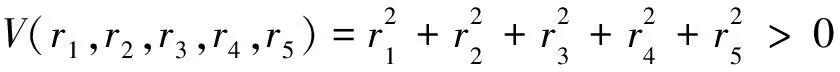
令V(r1,r2,r3,r4,r5)=K,很明显,当K是一正常数时,上式表示一球面,记为E。

求V的导数:

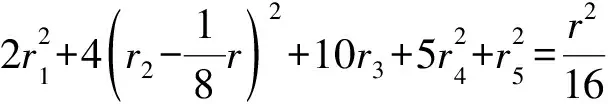
由式(14)可知:

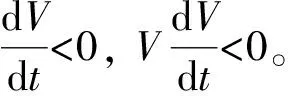
4 数值仿真

随参数r的变化,系统(9)的稳定性将发生改变, 将出现分叉和混沌等现象。如下图形均取x1,x2,x5这3个分量,其他分量可类似讨论.

1) 当r<8.3…时,轨道是稳定的螺旋线,环绕一点进行旋转,并且螺旋线越来越密集,最后变成极限环;当r>9.49…时,极限环失稳,分岔出新轨线,与原轨线形状相似,且与原轨线形成交叉环(图4)。这种现象和文献[1]中的r=28.6时是类似的。这种双轨道的情况不会立即消失,在r某一变化范围内存在。

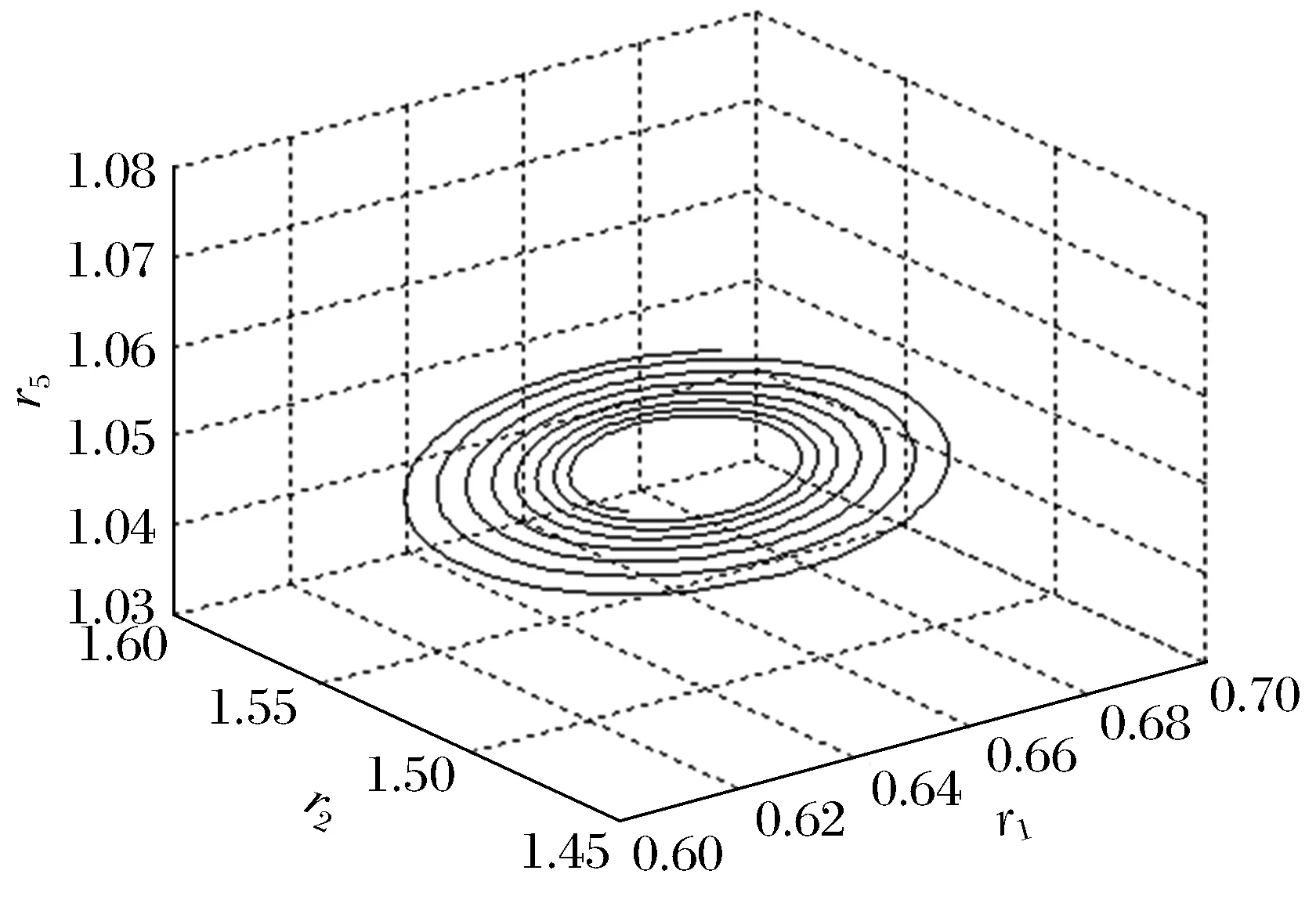
图1 (r=8.1)螺旋线Fig.1 (r=8.1)spiral

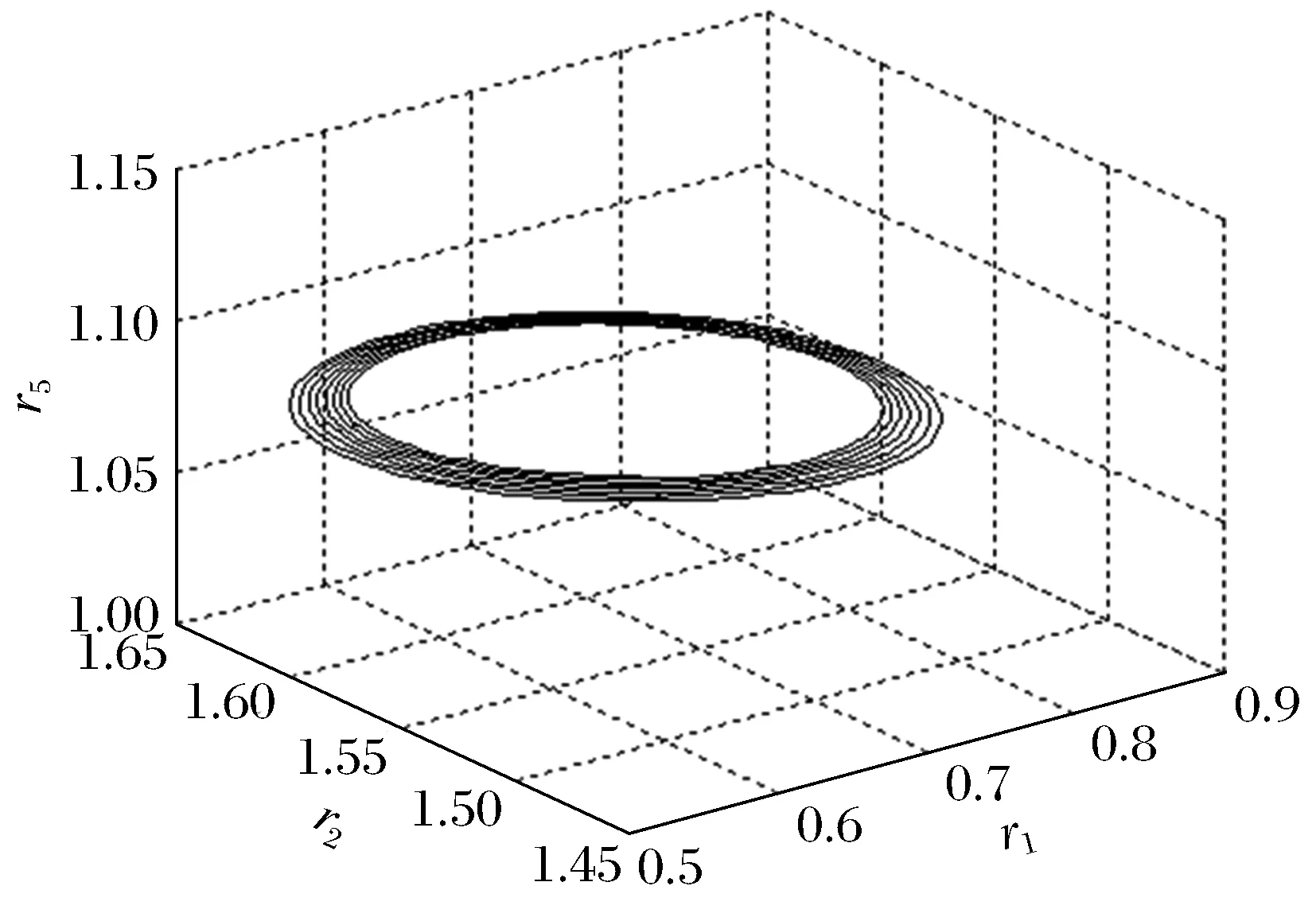
图2 (r=8.3)收缩的螺旋线Fig.2 (r=8.3)contractile spiral

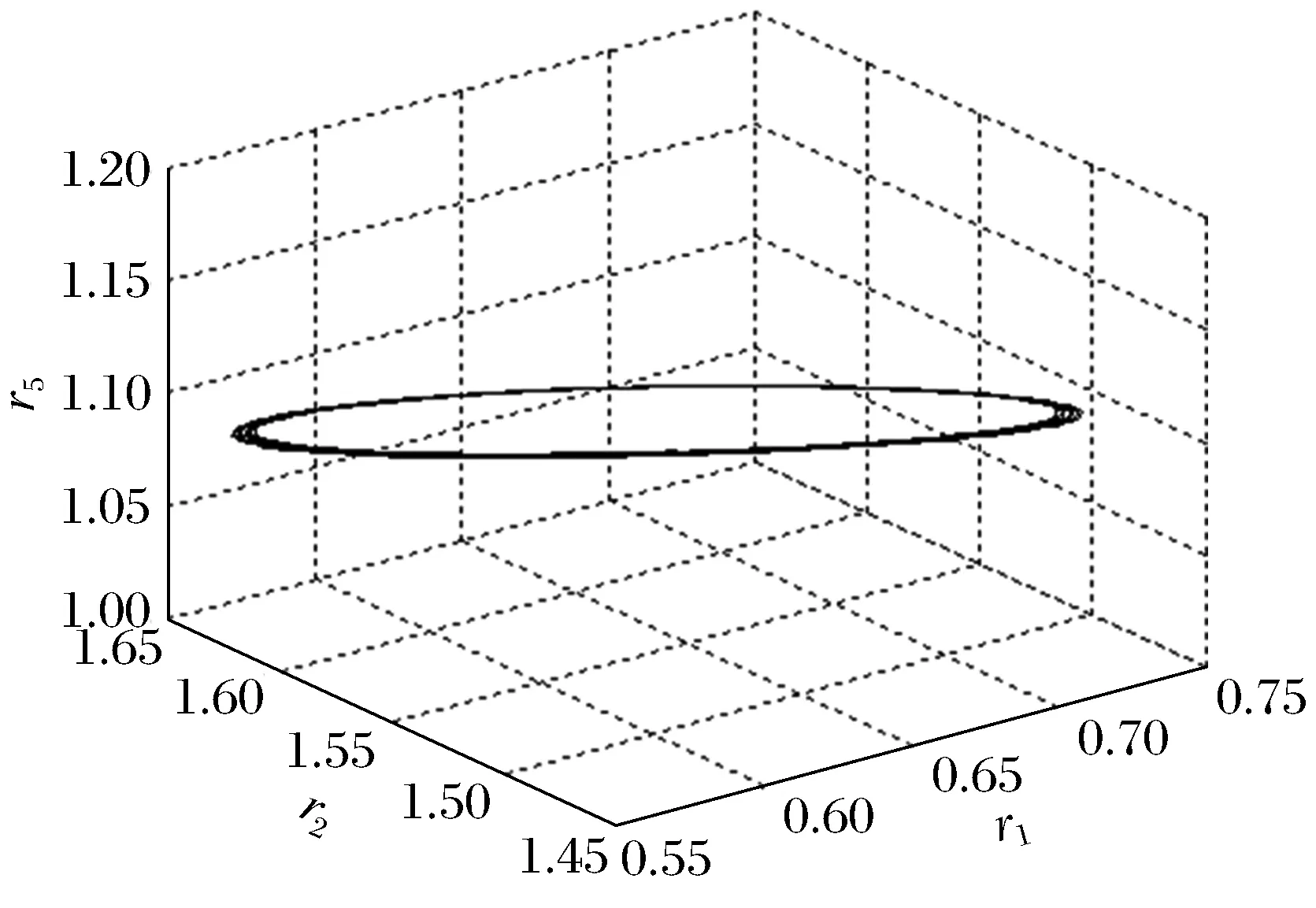
图3 (r=8.34)极限环Fig.3 (r=8.34)limit cycle

图4 (r=9.49)双螺旋轨道Fig.4 (r=9.49)double helix orbit

2) 当r=9.52…时,环形轨线出现新分支,环绕另一奇点旋转(图5)。从这以后环形轨线绕2个奇点来回环绕,产生奇怪吸引子。图6、图7、图8刻画了不同参数下奇怪吸引子的形态。

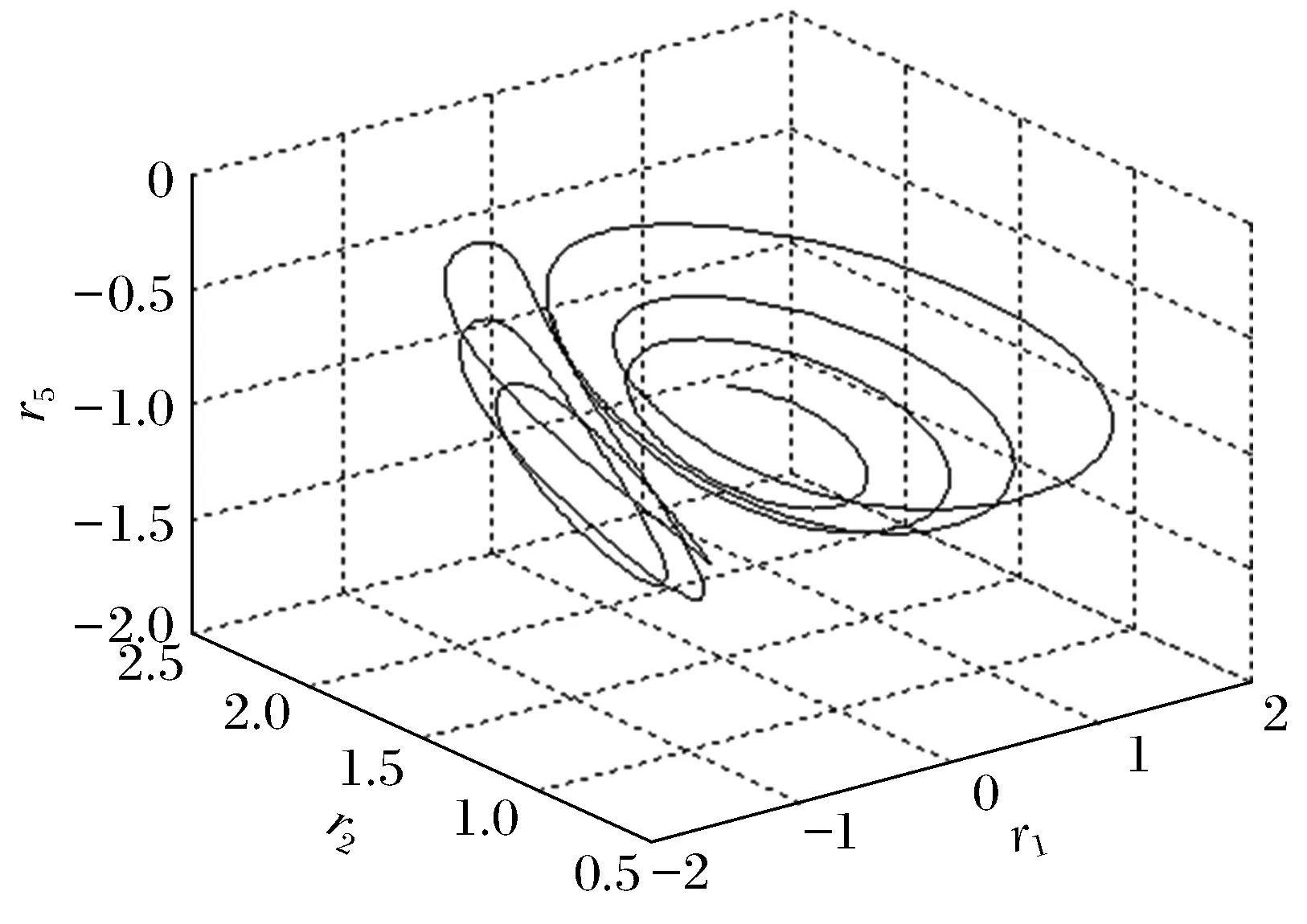
图5 (r=9.52)双螺旋轨道Fig.5 (r=9.52)double helix orbit

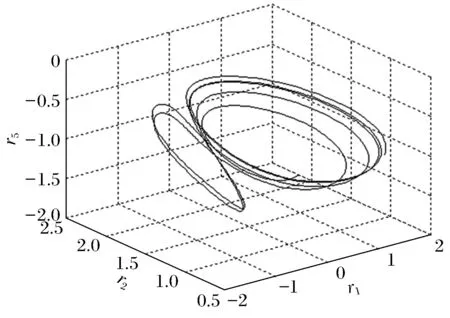
图6 (r=9.737)奇怪吸引子Fig.6 (r=9.737)strange atractor

图7 (r=9.809)奇怪吸引子Fig.7 (r=9.809)strange atractor

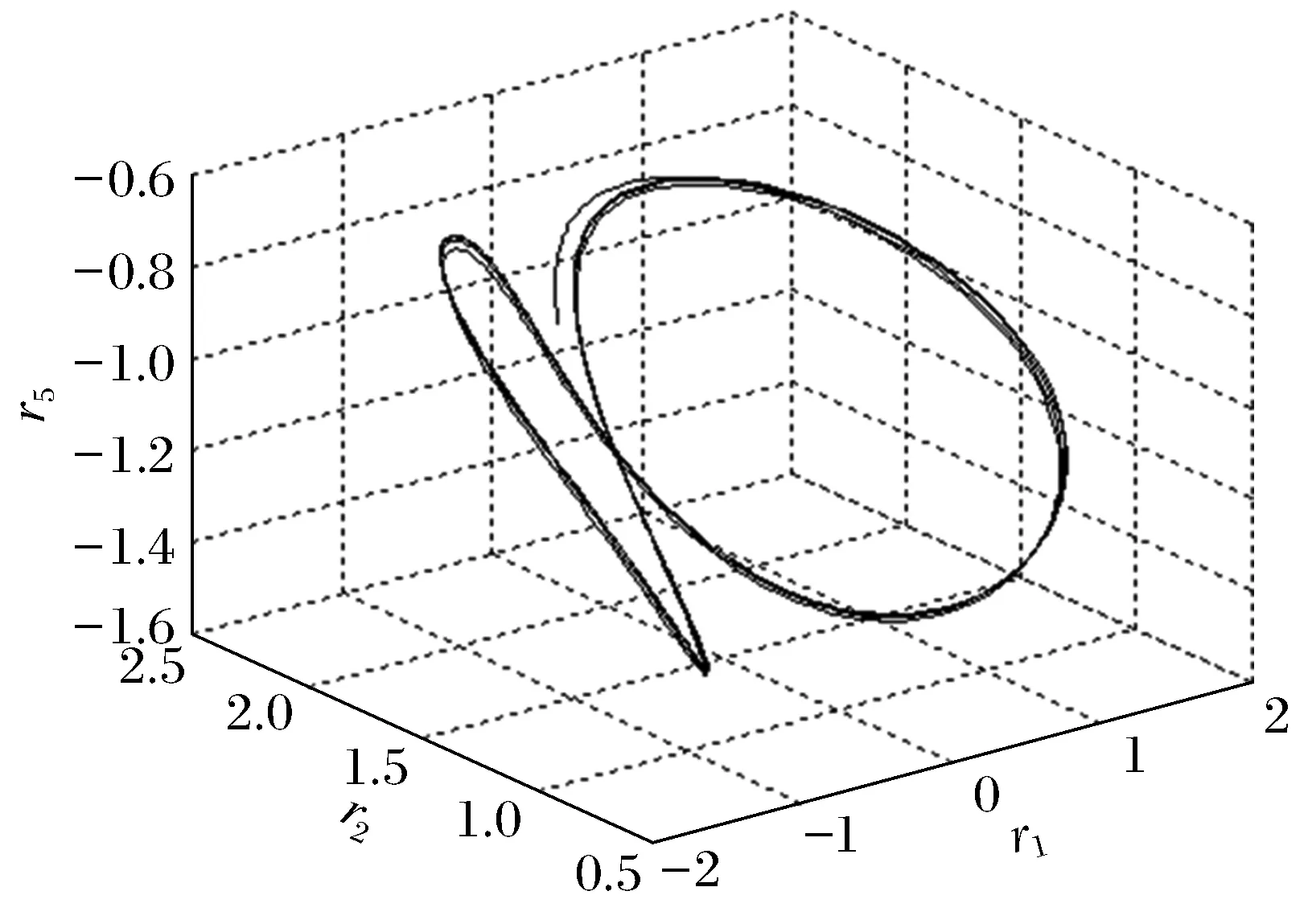
图8 (r=9.85)过渡轨线Fig.8 (r=9.85)transition trajectory

3) 当r=9.9…时,奇怪吸引子变为2个交叉极限环(图9和图10),以后保持这种状态很长一端时间,然后轨线逐渐演变为环面(图11和图12)。

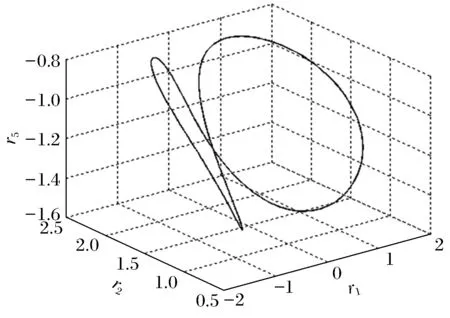
图9 (r=9.9)极限环Fig.9 (r=9.9)limit cycle

图10 (r=12)极限环Fig.10 (r=12)limit cycle

图11 (r=49)环面Fig.11 (r=49)torus

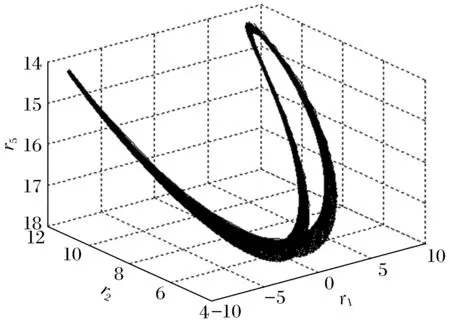
图12 (r=105)环面Fig.12 (r=105)torus

以上的仿真分析也进一步证实了混沌运动是确定性和随机性的对立统一,表明了它对初始状态的敏感依赖性。以上是无穷维系统有限维约化的一个简单例子,有兴趣的读者可进一步参考有关文献[11-15]。

5 结 论

本文对平面正方形区域上不可压缩Navier-Stokes方程进行有限维约化,得到新五维类Lorenz系统,通过稳定性分析和数值仿真,揭示了系统解的动力学行为。新约化模式及系统混沌行为的仿真具有一定的实际意义。