带有混合时滞的惯性神经网络系统的反同步控制

张国东, 龙常青

(中南民族大学 数学与统计学学院, 武汉 430074)

1987年, BABCOCK[1]首次把电感引入到神经网络中, 构造出了一种二阶惯性神经网络模型；并分析了该二阶微分方程的混沌、分岔等动力学行为.由于其在联想记忆、图像处理、信号处理、优化等领域有着十分广泛的实际应用, 近几十年受到了许多学者们的关注和研究, 并取得了许多丰硕的成果, 见文献[2]到文献[7].

另外, 由于网络系统的信号传送不是瞬时的, 并且网络系统具有分布式的空间结构, 这通常会导致时滞和分布时滞的存在, 因此把时滞和分布时滞考虑到神经网络模型中来是合理的.反同步控制, 即要求两个系统达到同步时, 它们的状态绝对值相同符号相反[8].在实际中, 如在通信系统中通过应用反同步控制在同步和反同步之间变换传输数字信号, 实现同步与反同步之间连续地传送数字信号, 加强安全和保密[9],截止目前, 神经网络的反同步控制问题已有一些研究, 如文献[8]基于Lyapunov函数和线性矩阵不等式研究了混合时滞神经网络的反同步.文献[9]基于集值映射和微分包含理论获得全局指数反同步的充分条件, 但对于带有混合时滞惯性神经网络反同步的研究很少涉及到.因此, 本文的结果将进一步补充该方面的相关研究.

1 系统模型及准备工作

令N={1,2,…,n},n,分别表示n-维欧式向量空间和实数集,([-ρ,0],n)表示在Banach空间中的所有连续函数组成的集合, 其中,ρ=max{τ,ω},∀μ=(μ1,μ2,…，μn)∈n, 定义范数([-ρ，0],n)其范数定义为：

在文献[2]的基础上, 我们考虑如下一类带有混合时滞惯性神经网络模型：

(1)

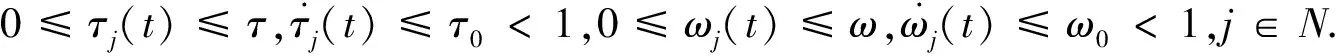
假设1 设模型(1)中的激励函数fj(·),j∈N, 是有界的奇函数, 并且满足Lipschitz条件:

|fj(s1)-fj(s2)|≤Lj|s1-s2|.

其中,s1,s2∈,Lj≥0.

(2)

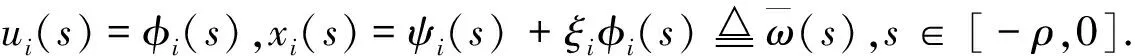
现将系统(2)作为驱动系统, 其对应的控制响应系统如下：

(3)

和初值为vi(s)=φi(s),yi(s)=ηi(s),s∈[-ρ,0],φi(s),ηi(s)∈是状态反馈控制器, 设计如下：

(4)

其中,πi≥0,ħi≥0是控制器增益常数.

现设e1i=ui(t)+vi(t),e2i=xi(t)+yi(t),i∈N结合(2)-(4)式, 则得到如下的闭环误差系统：

(5)

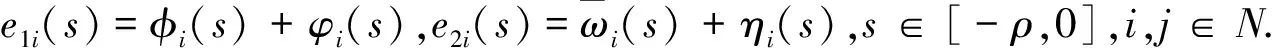
定义1驱动系统(2)和响应系统(3)称为全局指数反同步, 如果∃M≥1,0<ε<1满足：

这里i∈N,ε表示指数收敛率.

2 主要结果

1-βi+ξi-πi<0,

(6)

和

(7)

则在状态反馈控制器(4)下, 驱动系统(2)和响应系统(3)实现全局指数反同步.

证明构建如下的两个连续单调增函数

pi(ε1)=ε1+1-βi+ξi-πi,

和

qi(ε2)=ε2-ξi-ħi+|γi|+

这里,ε1和ε2是两个变量.从(6)和(7)易知pi(0)<0,qi(0)<0,i∈N, 又因为函数pi(ε1),qi(ε2)单调递增, 所以存在ε*使pi(ε*)=0和qi(ε*)=0.即∃ε∈(0,ε*), 使得下面两个不等式成立

ε+1-βi+ξi-πi<0,

(8)

和

ε-ξi-ħi+|γi|+

(9)

现在, 考虑如下的Lyapunov泛函:

(10)

计算函数V(t)沿着系统(5)解的右上Dini导数，则有

(11)

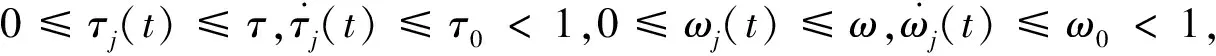
t≥0.

(12)

由(10)和(12), 可得：

|e2i(s)|]e-εt+

M(‖e1(s)‖+‖e2(s)‖)e-εt,

(13)

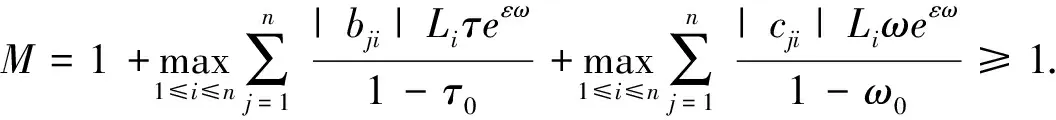
即证.

推论1假设1成立, 且τj(t)=τj>0,ωj(t)=ωj>0,j∈N, 若存在非负数ξi,πi和ħi,i∈N, 满足(6)式及下面不等式

则在状态反馈控制器(4)下, 驱动系统(2)和响应系统(3)实现全局指数反同步.

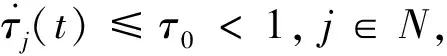
则在状态反馈控制器(4)下, 驱动系统(2)和响应系统(3)实现全局指数反同步.

3 数值仿真例子

现借助MATLAB工具, 本部分给出数值仿真来验证上述结果的有效性.

例1考虑一个二维惯性项神经网络系统如下：

(14)

其可以改写为

(15)

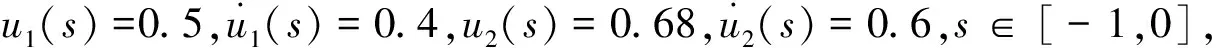
通过简单的计算易知,τ=ω=1,τ0=ω0=1/4,f1,f2满足假设1, 且L1=L2=1.将系统(15)为驱动系统, 其对应的受控响应系统是(3)式所定义.控制器(4)的增益常数取值为π1=4,π2=3,ħ1=13,ħ2=8.参数ξ1=ξ2=1, 则有

故定理1的全部条件成立, 则知驱动系统(15)和其响应系统(3)在控制器(4)下全局指数反同步.

取初值为u1(s)=0.5,x1(s)=0.6,u2(s)=0.68,x2(s)=0.6,v1(s)=0.4,y1(s)=0.8,v2(s)=0.68,y2(s)=0.6,s∈[-1,0).在控制器(4)下, 反同步误差系统状态变量趋向于零平衡点的轨道走势如图2所示.驱动系统(15)和响应系统(3)的变量u1(t),v1(t),x1(t),y1(t),u2(t),v2(t),x2(t),y2(t)曲线图分别如图3-6所示.

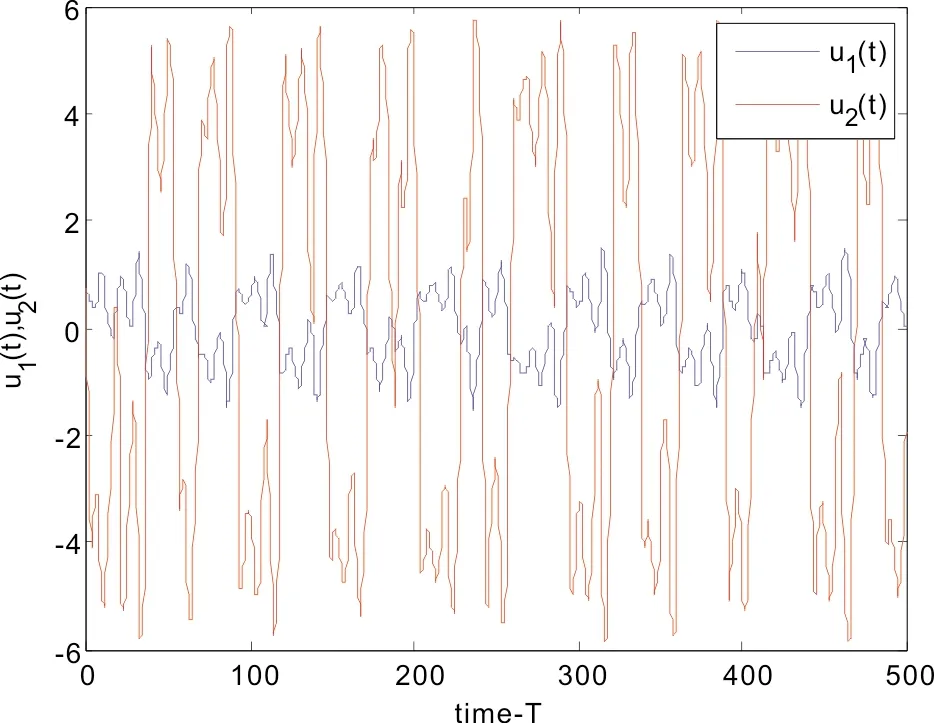
图1 无控制器下, 系统(14)状态变量u1(t)和u2(t)走势图

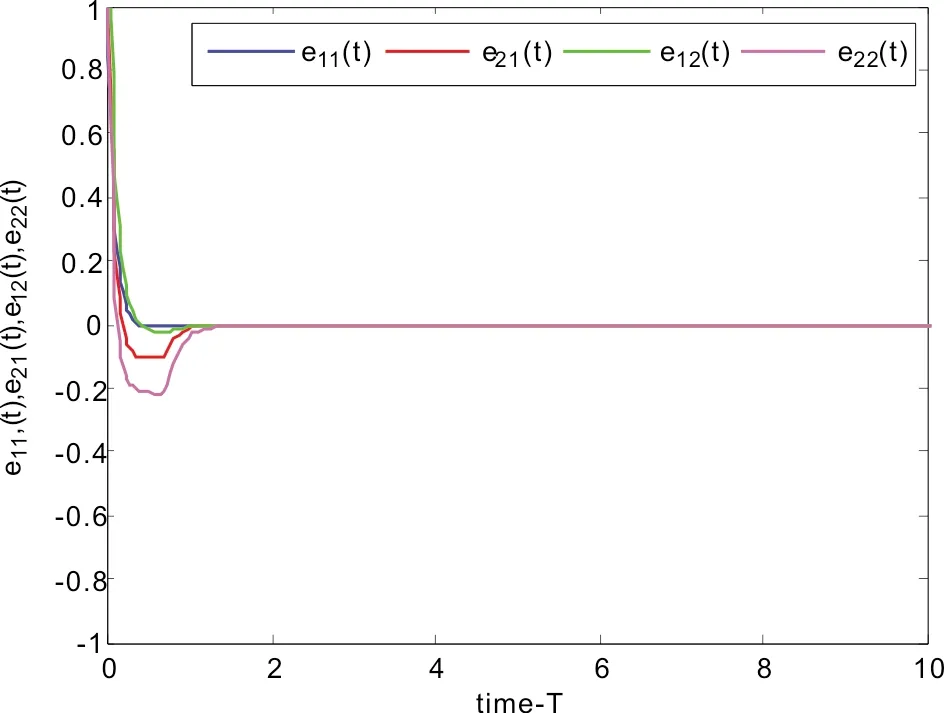
图2 在反馈控制(4)下, 反同步误差系统状态变量e11(t),e12(t),e21(t),e22(t)的走势图

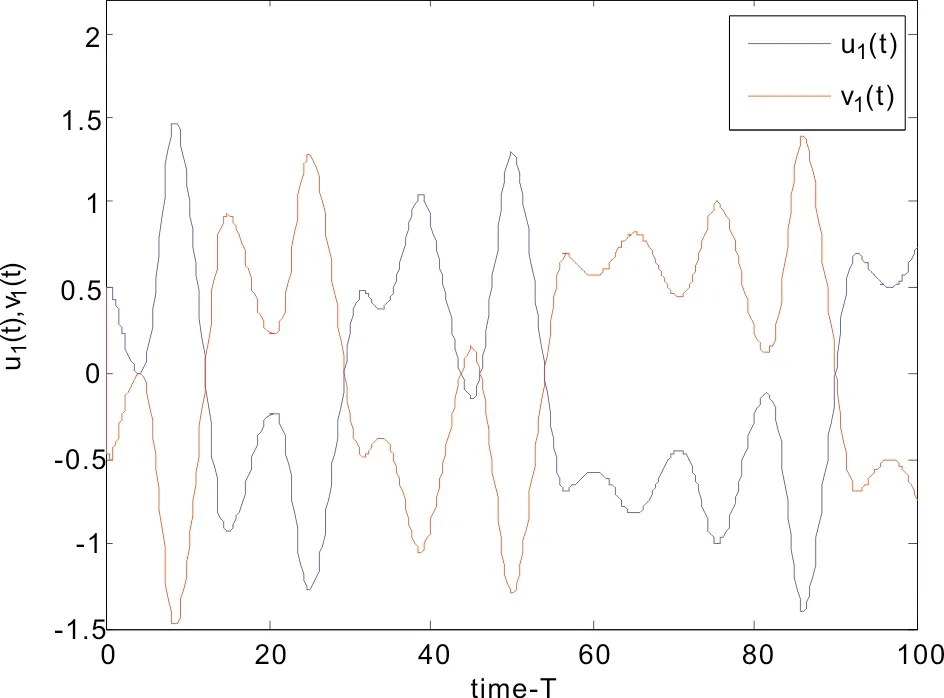
图3 在控制器(4)下, 反同步误差系统状态变量u1(t),v1(t)的曲线图

图4 在控制器(4)下, 反同步误差系统状态变量x1(t),y1(t)的曲线图

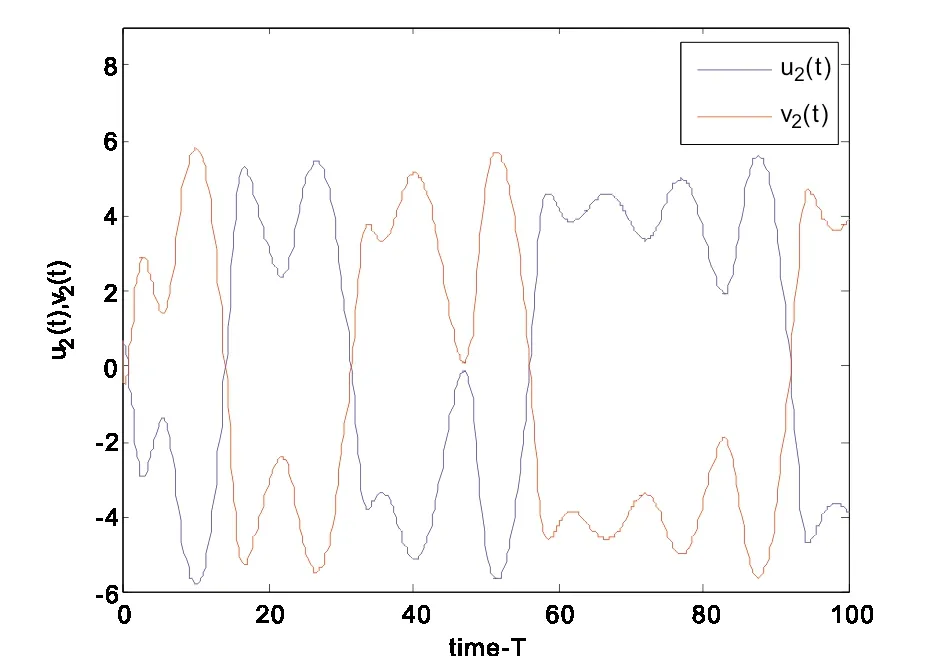
图5 在控制器(4)下, 反同步误差系统状态变量u2(t),v2(t)的曲线图

图6 在控制器(4)下, 反同步误差系统状态变量x2(t),y2(t)的曲线图

4 结论

在本文中, 利用降阶的方式和一些不等式技巧, 通过设计状态反馈控制器并恰当选择控制器增益使得具有混合时滞的二阶神经网络驱动-响应系统实现了全局指数反同步控制, 并得到了确保误差系统全局指数反同步的充分条件和几个推论.所得的结果由系统本身的参数给出, 容易验证和计算.最后, 给出了数值仿真例子验证所得结果的可行性.本文所得结果丰富了文献[2]的成果.