一类分数阶不确定奇异系统的保成本控制
2020-06-04杨占英张杰蔡明建
杨占英,张杰,蔡明建
(中南民族大学 数学与统计学学院,武汉 430074)
众所周知,分数阶系统[1-4]因其广泛的应用而备受关注.近年来,分数阶系统的保成本控制研究,取得了一些进展,如THUAN和HUONG在文[3]中研究了带时滞的分数阶神经网络的保成本控制问题;PHAT等在文[4]中给出了非线性分数阶时滞系统的保成本控制的新准则.
奇异系统(又称广义系统)由于能够同时包含状态变量之间的动态关系和代数关系,在描述更复杂的动力学模型方面有着重要应用.近几年,关于奇异系统的研究取得了丰硕的成果[5,6].对于分数阶奇异系统,也有一些文献进行了研究,如LIU等在文[7]中研究了一类分数阶非线性奇异系统的稳定性问题及其在复杂网络同步中的应用.然而,对于分数阶奇异系统的保成本控制问题,就作者所知,相关的研究目前尚未见报道.本文将研究一类分数阶不确定奇异系统的保成本控制问题.利用Lyapunov函数的性质和Schur互补引理,得到一种实现系统渐近稳定的保成本控制方案.最后通过数值仿真验证该方案的有效性.
以下使用到的符号:(X-1)T表示X-1的转置;矩阵X>0表示正定矩阵;‖·‖表示欧几里得范数,即:
1 准备知识
定义1[8]函数θ(t)的阶数为q的分数阶积分定义为:
其中q>0,Γ(·)是伽马函数,即:

定义2[8]函数f(t)∈Cn([t0,+∞),n)的阶数为q的Caputo型的分数阶导数定义为:
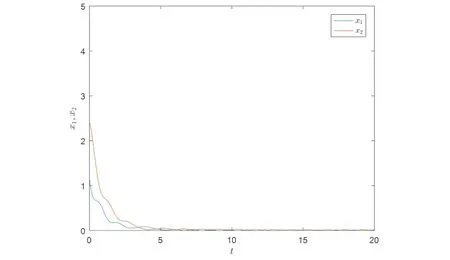
其中t≥t0,q>0,且n为正整数,满足n-1 命题2[10]设x(t)∈n是连续可导的函数.那么,对任意的t≥t0,有下列不等式成立: 其中P是正定矩阵. 下面给出一些必要的引理. 对任意满足F(t)FT(t)≤I的F(t)成立,当且仅当存在一个正常数ξ,使得: 引理2(Schurcomplementarylemma)[12]对于一个给定的实矩阵: (i)S<0; 引理3[13]设A∈n×n为复矩阵,A是非奇异的当且仅当存在非奇异矩阵X∈n×n使得: AX+XTAT<0. 考虑如下的一类分数阶不确定奇异系统: (1) 其中α∈(0,1),x(t)∈n是状态向量,n∈,u(t)∈m是控制输入,E,A∈n×n以及B∈n×m是给定的常数矩阵,且Rank(E)=r 设计如下反馈控制器: (2) 其中K1和K2是待设计的具有合适维数的矩阵. 首先考虑系统(1)的规范化. 引理4[13]不确定分数阶奇异系统(1)是可规范化的当且仅当: Rank[E,B]=n. 定理1系统(1)是可规范化的当且仅当存在非奇异矩阵V和任意矩阵H,使得下列条件成立: EV+VTET+BH+HTBT<0, (3) 在此条件下,有K2=HV-1. 证明根据引理4,易知系统(1)是可规范化的当且仅当存在增益矩阵K2使得矩阵(E+BK2)是非奇异的,再由引理3可知,(E+BK2)是非奇异的当且仅当存在一个非奇异矩阵V使得: (E+BK2)V+VT(E+BK2)T<0, (4) 取H=K2V,此时(4)式与(3)式是等价的.证毕. 下面考虑系统(1)的渐近稳定性问题. 根据定理1,系统(1)可改写为如下规范化系统: (5) 其中E1=(E+BK2)-1,A1=E1A,B1=E1B.同时,控制器可写为: u(t)=K1x(t). (6) 对于系统(5),其成本函数如下: uT(s)Ru(s)]ds,∀Tf>0, (7) 其中Q和R是给定的正定矩阵. 定义3对于系统(5),如果存在一个控制器和一个正常数J0,使得对所有的可容许不确定项,系统(5)是渐近稳定的,且成本函数(7)满足J≤J0,那么J0称为成本函数的上界,控制器(6)称为系统(5)的保成本控制. 定理2给定正定矩阵Q和R,如果存在矩阵P>0,具有合适维数的矩阵Y和正常数ε使得下列条件成立: (8) 证明令: V(t)=xT(t)P-1x(t). 显然有: λmin(P-1)‖x(t)‖2≤V(t)≤λmax(P-1)‖x(t)‖2, (9) 对V(t)求导得: xT(t)(A1+E1ΔA+B1K1)TP-1x(t)+ xT(t)p-1(A1+E1ΔA+B1K1)x(t)= (10) 成立时,可以得到: (11) 由引理1可知,存在一个正常数ε,使得(10)式等价于: (12) 在(12)式两端分别乘以PT和P,可以得到: (13) 由引理2可知,(13)式成立当且仅当: (14) 由不等式(11)可知,闭环系统是渐近稳定的.接下来讨论成本函数的上界.由不等式(10)有: (15) 在(15)式两边从0到Tf做积分,利用命题1,可以得到: V(Tf)≤V(0)-J,∀t≥0, 进一步有: J≤V(0)≤λmax(P-1)‖x(0)‖2:=J*,∀t≥0. 因此,成本函数满足J<λmax(P-1)‖x(0)‖2,且J*=λmax(P-1)‖x(0)‖2.证毕. 考虑如下不确定奇异系统: x(0)=(1.6,2.4)T. 利用Matlab LMI工具箱,易得到(3)式的解为: H=107×(-7.0496,-2.374), 由计算可得: K2=HV-1=(-0.0123,-0.4592), 因此可知系统(1)是可规范化的,进一步可以得到系统(5)的新的参数矩阵: 另一方面,(8)式的可行解为: Y=(-2.335,1.0508),ε=3.4276, 于是得到如下增益矩阵: K1=YP-1=(-2.926,0.6188), 根据定理2,系统(5)在保成本控制器u(t)=YP-1X(t)作用下是渐近稳定的,且J*=3.6338.状态变量的相关演化过程如图1和图2所示,它们反映出系统在保成本控制器作用下实现了渐近稳定. 图1 x1和x2的状态轨迹 图2 范数的状态轨迹 对于分数阶奇异系统的稳定性和控制问题,不少文献已进行了深入研究.然而,分数阶奇异系统的保成本控制问题还未得到解决.对于一类分数阶不确定奇异系统,本文基于系统规范化、Schur互补引理和Lyapunov函数的性质,设计了一种保成本控制器,得到了实现该系统渐近稳定的充分条件;最后,通过数值仿真验证了该条件的正确性和有效性.
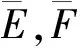

2 主要结果


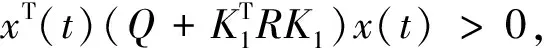
3 数值仿真
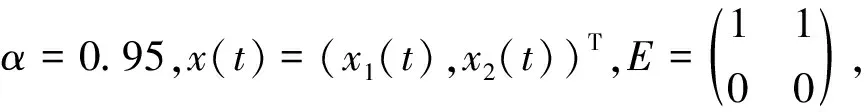



4 结论
