向思维更深处漫溯，让数学核心素养落地

胡小慧

从数学核心素养体系看，小学阶段培养学生数学思维的课程目标正是围绕数感、符号意识、空间观念、几何直观、数据分析观念、运算能力、推理能力等若干核心词展开。可以这样说，数学思维就是用数学的眼光看问题，用数学的思维想问题，用数学的表达交流问题，它是数学核心素养的内隐特质，是数学核心素养的灵魂，始终贯穿于数学核心素养的培养之中。正如郑毓信教授所指出的，“数学核心素养的基本含义就在于：我们应当通过数学教学帮助学生学会思维，并能使他们逐步学会想得更清晰、更深入、更全面、更合理”。

一、 “画图”在临界点，思维变直观

画直观图可以让复杂的问题变得简单，小学生处于直观思维向抽象思维过渡的阶段，画图的作用尤为明显。通过画图将学生内在的思维外显，进一步加深学生对知识的理解和内化。

在教学“两位数加两位数进位加法”时，教师没有让学生进行摆小棒操作活动，而是让学生根据“34+16”这个算式画小棒。

学生画完后，师生进行交流。

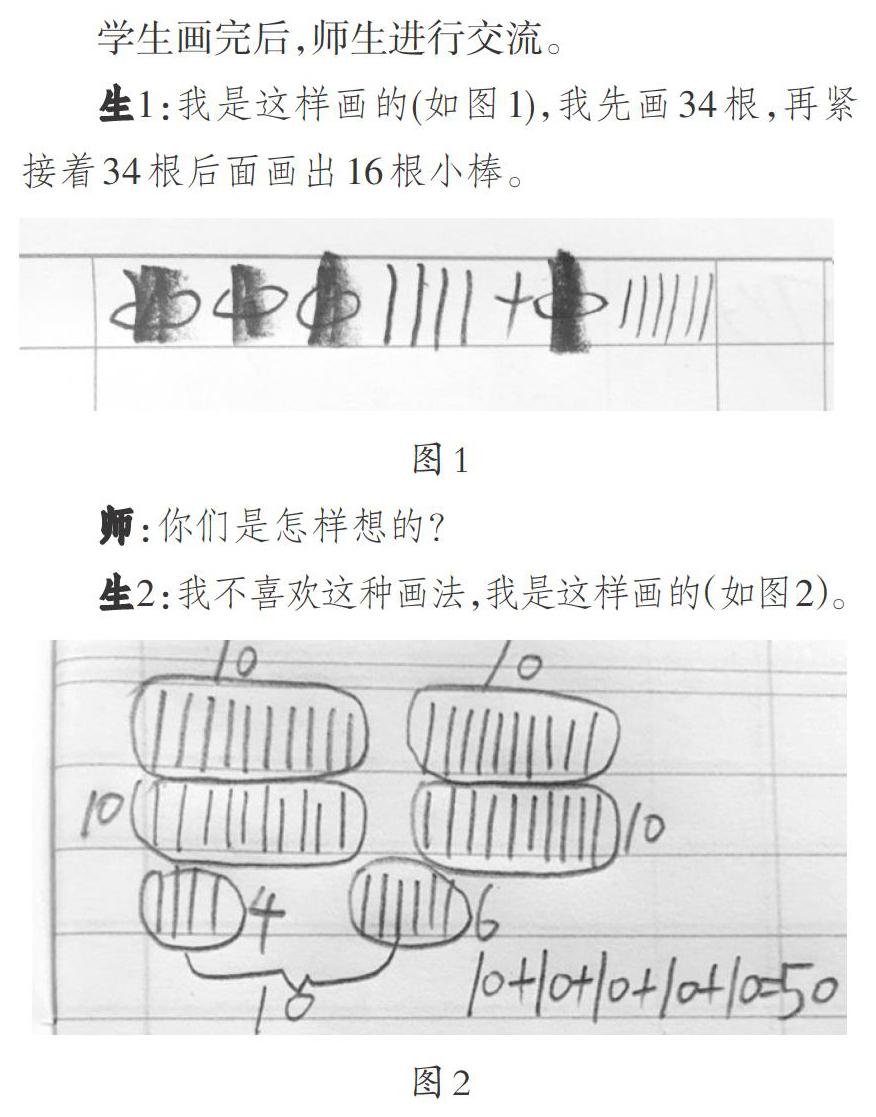
生1：我是这样画的（如图1），我先画34根，再紧接着34根后面画出16根小棒。

师：你们是怎样想的？

生2：我不喜欢这种画法，我是这样画的（如图2）。

上面是10根的，下面是单根的。4根加上6根是10根，所以合起来是50根。

生：我觉得他没有必要一根一根地画，10根就是一捆，可以一捆一捆地画。

师：有没有不同的画法？

生3：我是这样画的（如图3）。

师：这样画，你们认为怎么样？

生4：我觉得他应该整捆和整捆对齐，单根和单根对齐，我是这样画的（如图4）。这样大家一眼就能看出单根和单根合起来是10根，又可以捆成一捆。

生5：我觉得应该把捆成的一捆放到左边整捆的这边，这样一眼就看出合起来是5个10，是50。我是这样画的（如图5）。

这是学生“画”小棒引发的思考过程，展现了真实的思维活动过程，学生的表现具有差别性和多样性，有的在教师的预设之中，有的在教师的预设之外，教学中让学生与研究中的自己对话，并不断迸发思维火花，学生对两位数加两位数中“相同数位对齐”就有了更深的理解。

二、“机会”于交叉点，思维更进阶

我们要给学生提供开放的平台和载体，让学生成为“学习旅途”中丰富历练的“每一个”，从而真正让学生思维更进阶。

有这样一道题：1+2+3+4+5=（   ）×（   ），学生独立思考后交流。

生1：我是先算出它们的和1+2+3+4+5=15，所以后面括号里可以填3×5或者填5×3。

生2： 1+4=5，2+3=5，还有1个5，这样合起来是3个5，所以可以填3×5。

师：你的想法正确又快捷。

生3：还可以这样来想，1+5=6，6里面有2个3，2+4=6，也是2个3，2个3加2个3再加1个3合起来是5个3，所以可以填5×3。

学生响起了掌声，认同这种方法的合理性。

生4：我是这样想的，1+2=3，4+5=9，9里面有3个3，这样合起来是5个3。

……

学生积极思考，想出了多种不同的方法，学生的探索热情高涨，研究并未戛然而止。

师：如果题目换成1+2+3+4+5+6+7+8+9=（  ）×（   ）=（   ），你会填空吗？

学生马上报出得数：5×9=45，看来他们找到了规律。教师见机趁热打铁：你们能自己编这样类似的题目吗？自己会计算吗？

学生跃跃欲試……

一开始学生有点不知所措，经过认真思考之后才慢慢开始讨论、交流、倾听、合作，整节课学生都是在反复摸索、思考中拾级而上，原来点滴、片面的思维也渐渐完整、厚实起来。下课铃声响起时，学生仍然不舍离去。

此时，习题已经不再是一道孤立的题，而是知识间相互联系的桥梁，是激发学生思考的源泉，是推动学生能力发展的重要资源。在此基础上促使学生对数学问题的认识从表层走向深入，从单一走向多元。

三、“创意”在统合点，思维再生长

数学教学中，教师除了要重视基础知识和基本技能，使学生掌握分析问题的基本方法，更应该在知识的统合点融合各类知识，完善认知结构，形成知识体系，加强综合运用。

在教学“平均分”时，教师设计了一个创意教学环节：请你用自己喜欢的图形表示出平均分。

比如：我画了（）个图形，每（）个一份，分成了4份。

师：请同学们大胆地去想象，大胆地去创作，用彩笔记录下来。

学生积极创作，学生的一幅幅作品呈现在我们眼前。

我画了（8）个图形，每（2）个一份，分成了4份。

我画了（12）个图形，每（3）个一份，分成了4份。

我画了（20）个图形，每（5）个一份，分成了4份。

我画了（4）个图形，每（1）个一份，分成了4份。

我画了（16）个图形，每（4）个一份，分成了4份。

…………

师：观察这些作品，它们相同的地方在哪里？

生：都是把一些图形平均分成了4份。

师：它们不同的地方在哪里？

生：画的图形的个数不同，每几个一份的个数也不同。

师：如果要把这些作品排排队，你准备怎么排呢？

学生交流，学生排序……

师：你们真棒，就这样画一画，大家就创造出了这么多的有关“平均分”的作品。其实，我们的数学就是这样的神奇、这样的有趣。

这个创意教学活动注重了学生交流，让学生感受到了思维生长的每个瞬间。学生自觉地对探究、认知过程进行修正与补充，以达到对知识的深层次理解，使思维向纵深发展，提高了数学思维能力和数学素养。课堂教学的真正精彩，是学生学得精彩。教师要给学生充裕的思考时间，酝酿精彩;教师要给学生充分的交流时间，展示精彩。

四、“指导”在转折点，思维超独特

在数学学习过程中，因为个性差异，每个学生都有自己独特的思维方式。独特的思维方式能够提高洞察力和理解力，是创造性思维的重要特征。

在教学“从条件想起”时， 学生研读教材后，教师围绕“第一天30个，以后每一天比前一天多5个”这个关键条件做足文章，帮助学生理清题目意思，然后引导学生：先根据（    ）和（    ）求出（     ），再根据（   ）和（   ）求出什么，让不同层次的学生都有途径寻找解决问题的突破口，得到解决问题的机会。在交流的过程中学生明确先根据第一天的个数和第二天比第一天多5个求出第二天的个数，再根据第二天的个数和第三天比第二天多5个求出第三天的个数，以此类推求出第五天的个数。

在启发学生通过列表或列式计算的过程中，学生的思考并没有停止，通过看得数再次验证以后每一天都比前一天多5个，随后教师巧妙点拨：“你心中应该还有其他想法了吧？”有学生回答：“第五天有40+10=50个，第五天的个数比第三天多2个5。”瞧，学生的思路多清晰。教师紧接着追问：“如果是和第一天比呢？”学生回答：“30+20=50，比第一天多4个5。”从这里我们看见了学生的思维过程。

在回顾以上几种方法有什么共同的地方时，教师再次引导学生根据条件来思考，这就是解决问题的策略——从条件想起，通过问题图式化，学生自主建立解决问题的模型结构，让学生的表达更加清晰，让学生的思维看得见，让学生的思考更深刻、思维更独特。

以学生为主体的课堂，并不是教师完全放手，而是要有扶有放、扶放结合。这就要求教师要在学生疑惑、困惑、出现错误时加强指导，以有价值的问题、启发性的语言、丰富的活动等为支点引导学生思考。

就数学学习而言，教会学生用数学的方式去思维，向思维更深处漫溯，远远比数学知识本身的教学更有意义。因此，我们应当积极发展学生思维，培养学生数学核心素养。

（作者单位：江苏省丹阳市实验小学）