数形结合培养学生数学建模能力

何瑞林

著名数学教育家张奠宙先生指出：“就许多小学内容来说，本身就是一种数学模型……在这个意义上，我们每堂课都在建立数学模型。”教师在研究探索小学数学建模教学的过程中，要以具体的课例研究为载体，从学生的角度去思考，帮助学生建构数学模型和应用数学模型。

一、借助数形结合，让学生理解数学建模思维的本质

学生在学习人教版小学数学四年级上册“数学广角”的时候，他们对这一单元十分感兴趣，特别是比较聪明的学生，他们情绪高涨，而对于潜能生而言，由于教材编排的内容与生活联系较紧密，他们虽然有一定的兴趣，但建模思维难度较大，要想让这部分学生深入地思考并建立数学模型还有一定的难度，基于此，教师可利用数形结合的方法，让学生理解建立数学模型的本质。如例2“烙饼问题”教学：

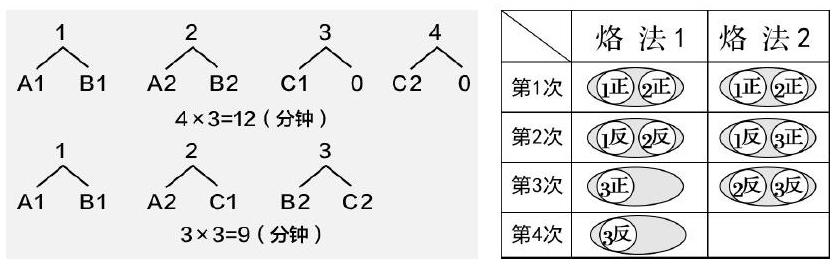
在这节课的教学过程中，教师让学生解决了“3 张饼”的最佳烙法这个问题后，再次提出时间到底节省在哪里？学生对于这个问题大多数的回答是次数减少了，时间就节省了，很多老师也觉得问到了这一步就是抓住了问题的本质，我认为有些偏差，那么怎样才能抓住问题的本质呢？我在教学中运用数形结合的方法，学生能比较容易地看出次数的多少和时间的关系，再让学生进行分析和对比，不仅让学生从次数的维度上进行考虑，而且能够更直观地从空间的维度进行更深一步的挖掘。（如图）

这样设计，学生能够从视觉上更加理解时间真正减少的原因是空间上的充分利用，这才是时间节省的真正本质。

二、利用数形结合，让学生经历数学建模思维的过程

如例1“沏茶问题”教学：

笔者多次参与县教研室组织的示范观摩课活动，而在例1“沏茶问题”的教学中，教师注意培养了学生的数学思维能力的发展，并注重了数学模型的建立，但过于强调的是数学模型的构建，忽视经历数学建模思维的过程，导致学生“知其然，却不知其所以然”。在这节课教学设计时，教师可以依据新课标所倡导的教学理念，让学生通过“经历”和“体验”数学思想和模型建构的形成过程，以学生平时帮家里做家务，有一定的生活经验作为教学的起点，利用数形结合的方法，把学生熟悉的“沏茶”作引例，通过自己设计沏茶活动的时间，再通过与同学交流，使学生初步体会不仅要考虑事情的安排顺序还要考虑可以“同时做”这两个思维的角度。先出示4道工序，让学生摆出沏茶的流程图，初步让学生感受事情的先后顺序和同时制作的方法，体会到同时做事情可以节省时间的理念。接水、烧水（烧水的过程中可以找茶叶、洗茶杯）、沏茶，让学生考虑有序地同时做事情。（如图）

在此基础上又出示“喝茶和洗茶杯各2分钟”，让工序增加到5步，让学生思考“为什么同样增加一件事情，一种方案的时间不变，而另一种方案的时间变了呢？”让学生就这个问题进行观察和比较，讨论自己是怎么安排的。

通过观察比较，进一步让学生体会事情发展的顺序和同时做的两种思维角度的不同，所以时间也会有所不同。这一次通过纵向的比较分析，让学生进一步明白同时可以完成的事情越多，那么越节省时间的道理。

学生在学习活动中不仅要思考怎样安排，而且要知道这样安排的原因，并动手画流程图，学生在设计的过程中自然地涌现出很多新奇的想法，通过自我经历—自觉生成—自我发现，进一步体验合理安排，体验运筹思想在日常生活中的应用，并建构出直观的数学模型流程图。在学生具备了一定的知识和方法的基础上，我出了这样一道题：妈妈下班回家做家务，淘米3分钟，煮饭15分鐘，烧水10分钟，洗拖把2分钟，拖地8分钟，如果只有一个炉子，妈妈做好家务至少要多久？我给学生创设了一个尝试、应用的空间，让学生在参与小组商议，探讨最佳方案的过程中感悟到合理安排时间做事，不仅要考虑时间，还要学会运用数形结合解决问题。

这个环节既是对前面学习的巩固，又引发了学生新的思考，让学生利用数形结合的方法，经历数学建模过程，带给学生的是探索中体验、创新中尝试、实践中会学，进而培养学生数学建模的能力。

总之，教师通过有目标、有层次地引领学生建构数学模型，在教与学的活动中，根据课例特点，利用数形结合的方法设计和指导，帮助学生经历数学建模过程。在体验学习中，教师还应结合课例采取形式多样、方法灵活的策略，让学生通过不断地自我构建，积累学数学、用数学的经验，使学生在体验、感知、讨论、合作、比较中灵活理解、掌握知识，由“学会”到“会学”，达到培养学生数学建模能力的目的。

（作者单位：河南省罗山县东铺中心校 ）