建构数学模型，搭建知识与运用之桥

鲁家宝

《数学课程标准》（2011年版）明确指出：“模型思想的建立是学生体会和理解数学与外部世界联系的基本途径。”数学是自然科学的基础，要想学好数学就要靠建模。小学数学是数学建模的基础，小学是数学学习建模的初始阶段，所以小学数学课堂教学要引导、帮助学生建构数学模型，这有利于促进数学教学观念、教学方法的改革。数学建模的本质是应用建构的数学模型来解决实际问题，是数学学习的一种新方式，它不仅关系到学生的学习，也关系到学生的终身发展。

一、“两次转译”是基本方法

数学模型是数学基础知识与数学应用之间的桥梁，建构和处理数学模型的过程，就是将数学理论知识应用于实际问题的过程。在建构数学模型的过程中，学生能体会到从实际情境中发展数学，获得再创造数学的好机会，进而形成新的数学知识。在小学数学教学中，让学生从现实问题情境中学数学、做数学、用数学，应该成为我们的一种共识，只有这样，数学教学中的“问题解决”才有了相应的环境与氛围。

“两次转译”基本方法可以帮助小学生自主建构数学模型，即把生活语言转译为数学语言，把数学语言转译为数学符号。数学建模活动的载体是数学建模素材——数学语言，选好建模素材，关系到整个建模的质量。数学来源于生活，又服务于生活，要将现实生活中发生的、与数学学习有关的素材及时引入课堂，将教材上的内容通过生活中熟悉的事例，以情境的方式在课堂上展示给学生，描述数学问题产生的背景，这样就能激发学生自己观察、发现、分析，把生活语言转译为数学语言，进而提出数学问题，为解决问题铺路架桥。数学建模是解决问题的一部分，也是解决问题的一种策略，它是对问题的分析、假设、抽象的数学加工过程，也是数学工具、方法、模型的选择与使用的过程，更是模型求解、验证、再分析、再改进、再求解的过程。数学建模需要数学概念、数学符号、数学运算等知识，数学建模就是使用数学符号、式子及数量关系对现实原型简化的本质描述，数学建模通过建立数学模型来解决问题。数学模型不仅为数学表达和交流提供有效途径，也为解决现实问题提供重要工具，可以帮助学生准确、清晰地认识、理解数学的意义，把数学语言用数学符号表示出来，进而解答问题。

二、“三步走”夯实建模基础

创设教学情境，提供建模信息。著名数学家华罗庚说过：“唯一推动我学习的力量，就是兴趣。”数学是充满乐趣的学科，教师要选准新知识的切入点，将抽象的数学融入一定的情境中，从现实生活的事例引出研究内容，这不但可以激发学生自主建模的兴趣，而且可以增强学生用数学的眼光观察生活、事物，用已有的知识解决实际问题的意识。让学生从数学的角度去思考，以此发现丰富的数学信息，为学生步入互动生成的课堂并乐于建构数学模型打好基础。

分析数量关系，形成建模过程。只有搞清楚数量关系才能根据四则运算的意义恰当地选择算法，把数学问题转化成数学式子。分析数量关系是帮助学生建立数学模型的关键。数学建模是对数学思想方法的提炼与概括，也是对数学知识梳理的过程，数学知识的掌握不是教出来的，而是自己动手实践总结出来的。数学建模正好是一个学数学、用数学的过程，它体现了学与用的统一。

运用四则运算的意义，构建数学模型。小学数学四则运算的意义是解决问题、构建数学模型的基础。学生在建构数学模型的过程中，运用四则运算的意义，联系数学猜想、推理论证、综合分析、概括抽象、实验操作、综合提升等思维，增强了科学探究的能力。教师在这一过程中引导学生自主建构，让学生在学习过程中形成构建数学模型的意识，用数学符号建立方程、不等式、函数等表示数学问题中的数量关系和变化规律涉及的符号意识、代换意识、方程思想、函数思想等，不仅帮助学生打开解题思路，培养他们的发散思维，开发不同学生的潜能，而且促使学生自觉地运用数学知识去思考和处理日常生活、生产中所遇到的问题，从而养成良好的思维习惯。

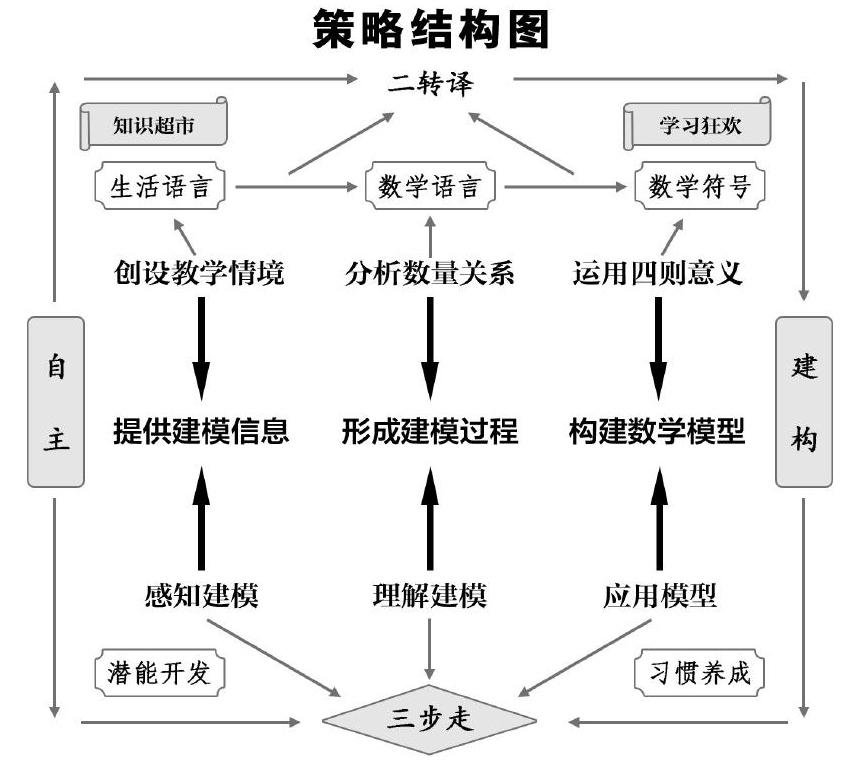
三、构建策略结构图

在小学数学教学中，学生的数学建模意识与核心素养培养相辅相成、密不可分。这就要求教师系统性地把“两次转译”“三步走”基本策略结合在一起，巧妙、灵活地依据教材内容，联系学生的认知水平有效设计教与学的过程。

综观策略结构图，不难看出，数学建模就是使用数学符号、式子及数量關系对现实原型简化的本质描述，数学建模就是通过建立数学模型来解决问题的方法，帮助学生准确、清晰地认识理解数学的意义。学生只有经历自主构建过程，数学思想、方法才能沉积、凝聚，从而使知识具有更大的智慧价值。

在教与学的过程中，教师尊重学生的个性，营造一种自主建构、合作交流的氛围，让学生在建构与交流中，开启心智，启迪智慧潜能。建立模型是创造，设计模型也是创造，而模仿模型、应用模型则是快速完善、快速发展的需要。数学模型是数学基础知识与数学应用之间的桥梁，建构和处理数学模型的过程，就是将数学理论知识应用于实际问题的过程。建立模型思想是学生体会和理解数学与外部世界联系的基本途径，也是学生深化、掌握和发展数学与外部世界联系的基本方法，是学生学习数学、学会数学、会学数学、应用数学的基础。

（作者单位：河南省罗山县教育体育局教学教研室）