变难为易，化繁为简

黄冰冰

【摘要】在小学数学教学中，教师要有目的地注意渗透数学思想方法。本文结合教学实践，从转化的基本模式入手，分从新知到旧知、从不等量到等量、从两个变量到一个变量三部分，就如何在小学数学低年级的教学中渗透转化的思想方法进行简单讨论。

【关键词】低年级 数学教学 数学思想 转化方法

数学思想是对数学内容和方法的本质认识和进一步抽象概况，它既是在具体教学内容中提炼上升的数学观点，也是在具体的数学活动中解决问题的根本看法，是建立数学、发展数学和应用数学解决问题的指导思想。数学方法是从数学的角度提出问题、分析问题、解决问题所采用的各种方式、手段和途径的总和。数学思想和数学方法都是以一定的数学知识为基础，反过来又促进学生对数学知识的理解和数学能力的发展。当前世界小学数学教育发展的趋势之一就是数学思想方法的渗透，做好这一工作，不仅可以使学生更好地理解数学知识，提高数学素养，也能为其将来解决社会中可能面临的实际问题打好基础。

在小学数学教学中，教师要有目的地注意渗透转化、分类、数形结合、归纳、方程等数学思想方法。本文旨在结合教学实践，就如何在小学数学低年级教学中渗透转化的思想方法进行简单讨论。转化的思想方法也叫化归的思想方法，其基本思想是用联系、运动和发展的观点去看问题，通过变换问题形式，把未解决的或复杂的问题归结到已经能解决的或简单的问题中，从而获得对原问题的解决。掌握转化的数学思想方法，对于小学生的数学学习和发展具有十分重要的作用。

在小学数学教学中渗透转化的思想方法，首先要了解转化的基本模式，在刘加霞主编的《小学数学课堂的有效教学》一书中对转化的基本模式做出如下解释：

在此模式下，教师要注重引导学生分析新问题中无法解决的困难，并相应运用策略将新问题转化为已经能够解决的旧问题，在解决旧问题的基础上解答新问题。通过学生学习经验的积累，使学生在探索解决问题的实践过程中，逐步认识理解转化这一抽象的数学思想方法。下面，就从几个教学案例中谈谈如何在小学数学低年级教学中渗透转化这一数学思想方法。

一、从新知到旧知转化

在苏教版小学数学二年级上册的除法运算的教学中，利用乘法口诀求商这一运算方法体现了转化的数学思想方法，即将学生面临的新问题——除法求商，通过转化，变为能够运用学生已经学习过的乘法知识解决的问题。但是，由于数学思想方法通常较为抽象，因此在教学中，教师很难通过语言讲清楚，更多的还是要通过学生经历一个数学学习的过程，在学习过程中感悟转化的数学思想方法。

例如，在教学口诀求商的时候，教师可以在学生探索计算方法前，先复习乘法口诀表，然后再出示复习题“2×（  ）=8”

“3×（  ）=15”和“（  ）x4=28”。通过乘法口诀的复习，让学生对已经学习的乘法口诀进一步熟悉。在非常熟悉乘法口诀之后，引导学生利用乘法口诀，解决在已知一个乘数和积的情况下，求另一个乘数是多少的问题。当学生已经能够很好地解决这一类问题后，再遇到除法中要求计算商是多少的问题时，就能将这一问题，通过理解，转化成求乘法口诀中另一个乘数是多少的问题，进而通过想乘法口诀来求商。比如，在计算9÷3=（）时，就是要算3个几是9，学生就可以想乘法口诀“三（）得九，商是（）”来计算。这一过程，虽然学生很难将整个思考活动用语言表述清晰，但学生所经历的算法学习的过程，就是运用转化这一数学思想方法解决问题的过程，只要教师注重引导，积极建立新旧知识之间的联系，就能帮助学生感悟转化这一思想方法的本质。

二、从两个变量到一个变量的转化

△+0 =12

△=0+0+0

那么△= （  ），0=（  ）。

这是一道一年级的数学思考题，学生在解题的过程中，遇到的问题主要是两个等式无法直接进行计算。这时，可以通过将两个变量转化为一个变量的方法，求解两个图形分别代表的数是多少。在师生共同探究的过程中，教师首先提问：“第一个算式能计算出三角形和圆是多少吗？”学生很自然地表示无法计算，因为既不知道三角形是多少，也不知道圆是多少。这时，教师进一步追问学生：“如果知道三角形是多少，或者圆是多少，是不是就能求出另一个图形表示的数是多少了呢？”在学生表示认同后，最后提示“仔细观察第二个算式你能知道什么”，这时数学学习能力强的学生已经可以思考得出，1个三角形等于3个圆，所以1个三角形加1个圆也就相当于4个圆，是12。这样一来，就将这一新问题转化为“4个几相加得12”的旧问题，学生在解决时自然就不存在困难，通过计算最终得出1个圆等于3，1个三角形就等于9。

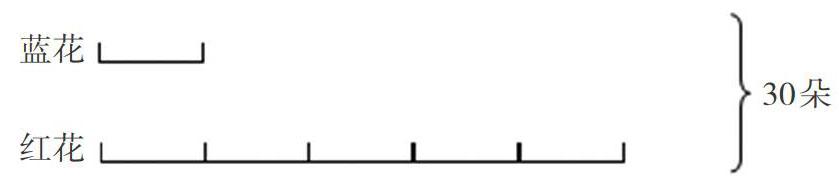
再如，学生学习“认识倍”以后，经常会遇到类似这样的问题：红花的朵数是蓝花的5倍，红花和蓝花一共有30朵，红花和蓝花各有多少朵？这种类型的“和倍问题”实际上就是运用转化的思想，将两个变量转化为一个变量进行计算。为了让低年级的学生更直观地理解解题的方法，还可以利用线段图辅佐讲解。（如下图）

在解决这道问题时，学生其实也是面临两个变量都不知道的情况，只有将其中一个变量進行转化，使得题目最终只剩下一个变量的时候，才能根据条件“30朵”计算出结果。根据倍的知识，学生可以看出将蓝花看作1份，红花有这样的5份，合起来就是6份，是30朵。这样一来，这一问题就可转化为“6个几相加得30”，学生根据以往的学习经验，可以顺利求得l份就是5朵，蓝花即5朵;5份就是25朵，红花即25朵。

这两题分别出现于一年级和二年级，但从解题的思路上看，都是利用了将两个量转化为一个量的策略，由此也可看出，转化这一数学思想方法是贯穿于小学数学各个年级的学习中的。

三、从不等量到等量的转化

将新问题转化为已知的旧问题的第三种模式——从不等量到等量的转化，在多种类型的问题中常会运用，即等量代换，上文所提及的两道例题也可看作是从不等量到等量的转化。此外，除了将两个量通过等量代换转化为一个量，还可以进一步在三个量、四个量等多个量之间进行代换，从而将复杂的问题转化为简单的问题进而解决。

例如，在解决问题“2只鸡的重量等于1只兔的重量，1只兔的重量等于4只鸭的重量，1只鸡的重量等于几只鸭的重量”时，可以利用等量代换的方法，将题目中的三个量相互联系起来。在解题时，教师可通过一系列的追问，引导学生主动思考，在解题的过程中体会转化的数学思想。以下是当时的教学片段：

师：第一个条件告诉我们什么？

生：2只鸡的重量等于1只兔的重量。

师：问题要求1只鸡的重量等于几只鸭的重量，那把兔换成鸭就好了！

生：可以换啊！ 1只兔的重量等于4只鸭的。

师：那第一个条件就可以替换成什么呢？

生：2只鸡的重量等于4只鸭（的重量）。

在这样的条件替换后，题目就转化成了“2只鸡的重量等于4只鸭的重量，1只鸡的重量等于几只鸭的重量”。通过这样的转化，解题思路也就跃然纸上了——鸡与鸭的数量同时除以2，1只鸡的重量等于2只鸭的重量。

以上，是笔者在小学数学低学段教学中对于渗透转化这一数学思想方法的一点思考。利用好每一道练习题，注重在解题过程中渗透相应的数学思想方法，可以为学生中高年级学习掌握“解决问题的策略”这一内容打下基础。从低年级开始，逐步渗透数学思想方法，也有利于学生整个小学学习阶段数学素养的提高。