回转齿轮箱故障特征提取的CMF-EEMD方法分析

魏香林

(广东创新科技职业学院机电工程系，广东 东莞 523960)

小波分解算法是一种分析故障振动信号的常用方法，其运算量较大，直接影响故障信号处理效率。小波分解算法具有传统小波算法的时频局部特点，可以体现振动冲击的周期性变化规律[1-3]。例如，当轴承表面由于腐蚀或应力破坏而产生凹坑时，会在齿轮传动系统运行过程中对齿面造成冲击，而这种冲击间隔刚好与轴承故障的周期相对应[4-6]。

为了克服小波分解算法在故障分析方面的缺陷，本文设计了一种由CMF-EEMD共同组成的带通滤波器。组合模式函数(composite mode function, CMF)其实是对滤波器的重新组合及分类，从而使原始信号被分解为高频与低频部分。以CMF作为集合经验模态(ensemble empirical mode decomposition, EEMD)前端滤波器，并通过适当调节白噪声幅值的方法来提升EEMD分解精度[7-8]。本文首先利用CMF将相邻的有限个本征模函数(intrinsic mode function，IMF)叠加，然后通过EEMD对循环自相关函数进行解调分析。采用CMF-EEMD信号处理方法诊断风电齿轮箱故障时还能够高效分离出不同状态下对应的故障特征频率。

1 CMF-EEMD基本原理

1.1 CMF

信号经EEMD分解得到C1,C2,…,Cm，包含了从高到低不同的频带，CMF将相邻的IMF叠加组成高频Ch和低频Cl。

Ch=C1+C2+…+Cm

(1)

Cl=C1+m+C2+m+…+Cn+m

(2)

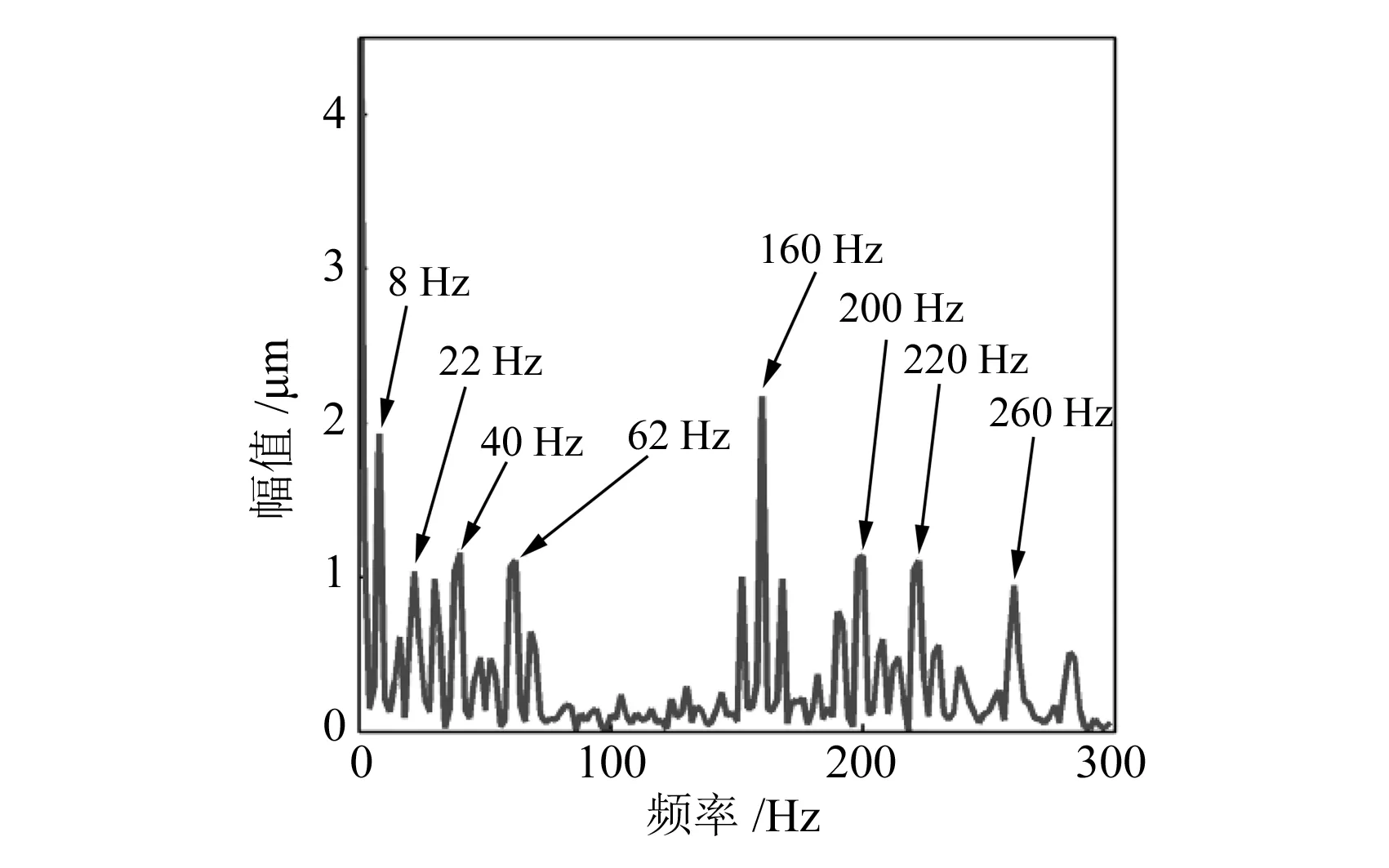
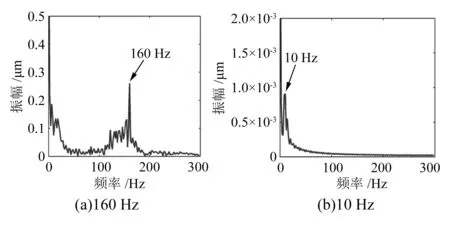
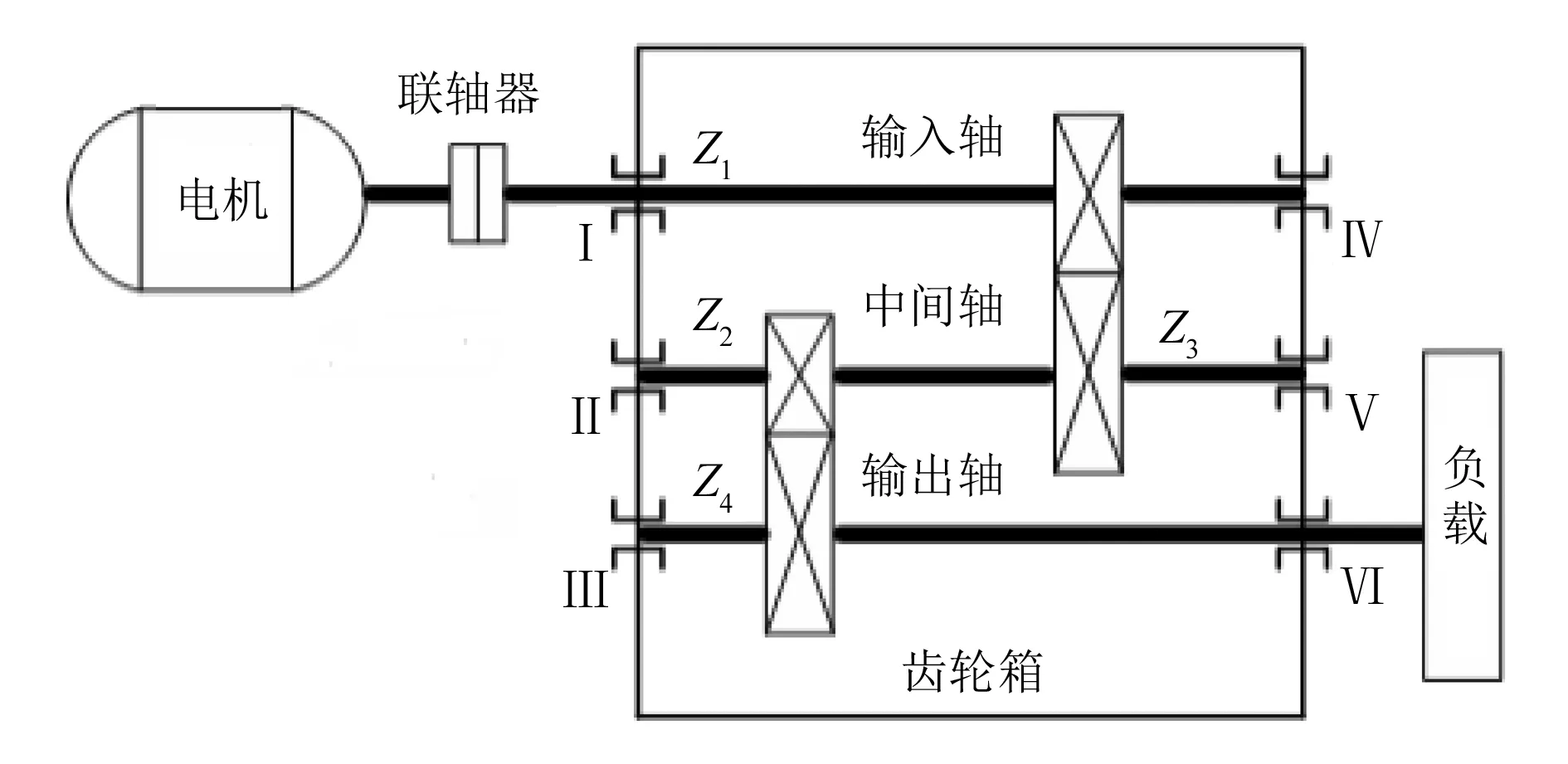
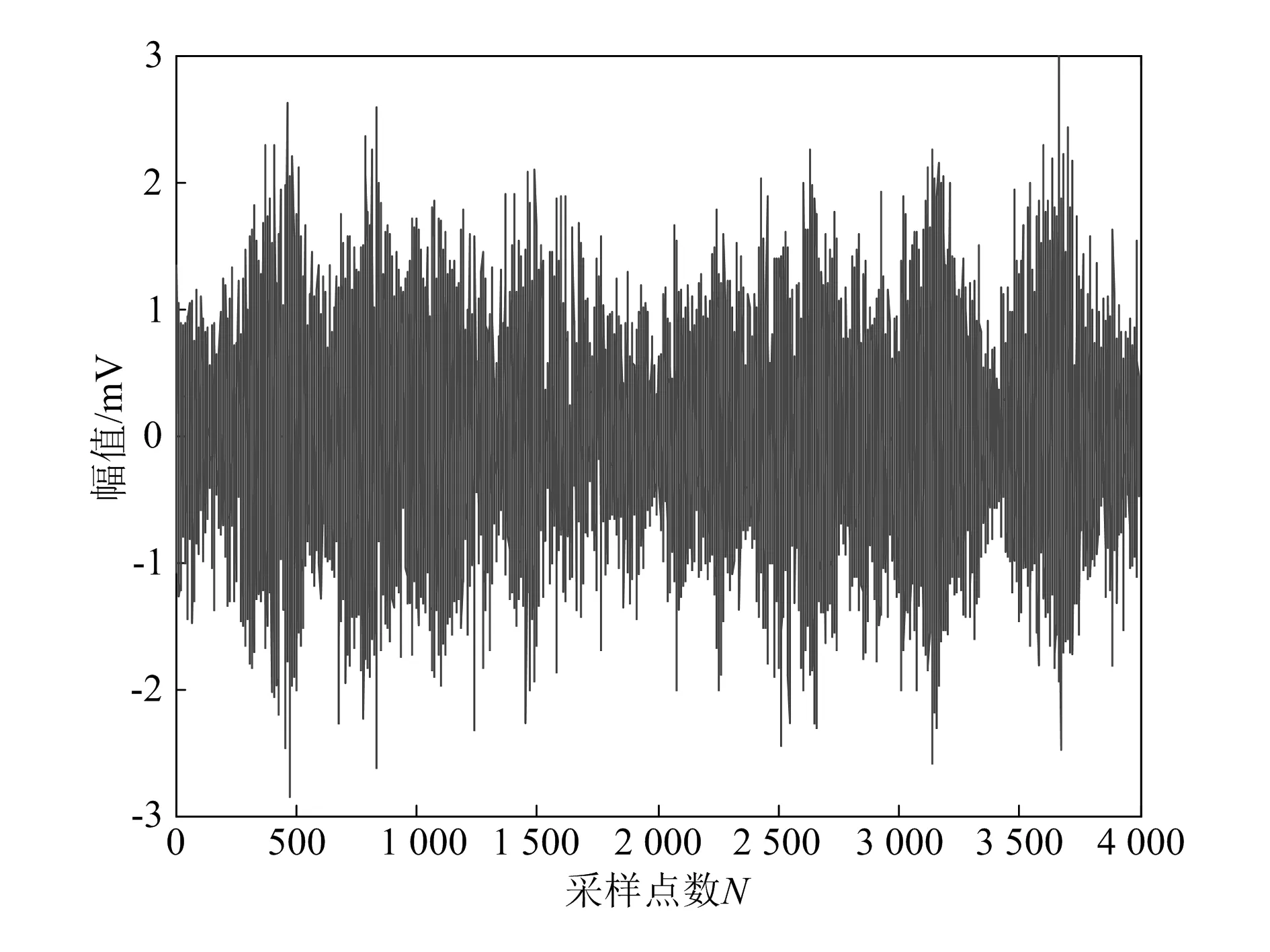
式中：m为含有高频IMF的最大层数；m

1.2 EEMD

EEMD中由于极值点分布不均导致模态发生混叠，EEMD的计算步骤如下：

1)给定一个原始信号x(t)，加入均值为零、幅值标准差为常数的白噪声nj(t)，j=1,2,3,…,M，M为样本数，则测试信号xj(t)与原始信号的关系为：

xj(t)=x(t)+nj(t)

(3)

2)用EMD分解xj(t)得到I个Ci,j，其中Ci,j为第j次加入白噪声幅值后分解得到的第i个IMF。

3)如果j

4)将上述IMF进行总体平均运算，则平均频带参数Ci计算公式如下：

(4)

5)输出Ci(i=1,2,3,…,I),得到的第i个IMF。

2 仿真实验分析

为了获取回转齿轮箱的故障信号特征，需对其进行解调分析。比如，先设定一个由多调制源以及多载波频率组成的仿真信号x1(t)，该信号共包含1 024个采样点，采样频率fs=600 Hz，调制频率fn1=8 Hz，fn2=15 Hz，fn3=10 Hz，fn4=12 Hz，载波频率fz1=80 Hz，fz2=130 Hz。

x1(t)=2[1+cos(2πfn1t)+cos(2πfn2t)]· cos(2πfz1t)+2[1+cos(2πfn3t)+cos(2πfn4t)]· cos(2πfz2t)+0.7noise(t)

(5)

式中：noise(t)为白噪声变化函数。

图1为仿真信号时域波形，图2为循环自相关函数的解调结果，可以明显看到循环频率fn1=8 Hz与2fz1=160 Hz属于主频部分，而高频段的2fz2=260 Hz未形成明显谱峰，但形成了200 Hz与260 Hz交叉项；低频部分fn3+fn4=22 Hz、2(fn1+fn4)=40 Hz、2(fn2+fn3) +fn4=62 Hz依次对应调制频率相加的结果。

图1 仿真信号时域波形

图2 循环自相关函数的解调结果

为了能够对特征频率进行精确提取，对信号调制系数c=0.2情况下的仿真信号EEMD进行分解，并实施快速傅里叶变换(fast Fourier transform, FFT)，处理结果显示前两层属于高频部分，包含了多种复杂频率并且分辨率较低。之后对相关性强的高频段频率以及低频段频率实施了循环自相关解调，结果如图3所示。其中高频区160 Hz属于仿真信号的载波频率，低频段区10 Hz属于原始信号调制频率。可以明显发现，经过FFT处理后仿真信号显著优于原始信号。同时还可以看到，在160 Hz的高频段仿真信号并未分解。

对图3中EEMD分解信号进一步进行高低频解调分析，可以得到如图4所示的结果，其中高频区为160 Hz,低频区为10 Hz。可以将上述结果作为提取实测信号特征的重要参考依据。

3 工程应用

为了测试齿轮箱的保持架故障信号，进行了故障信号提取实验。实验在齿轮箱故障诊断测试平台上完成，图5给出了齿轮箱故障诊断测试平台的具体结构。首先对输入轴部位的轴承保持架设定故障并完成安装。将齿轮箱转速设定为1 200 r/min，同时加载所需的载荷。然后将振动传感器放置在齿轮箱I处，通过多功能数据采集系统(LMS)采集此处的振动数据，设定采样频率为4 000 Hz，采样间隔为100 s。轴承参数见表1 ，此轴承故障特征频率为13 Hz。

图3 仿真信EEMD分解结果

图4 160 Hz和10 Hz的信号解调分析结果

图5 齿轮箱故障诊断测试平台的具体结构

表1 轴承参数表

图6给出了保持架故障信号时域图。由图中的振动信号可以发现，齿轮箱在运行阶段形成的振动冲击信号幅值发生了明显变化，可以初步判断该齿轮箱发生了故障。不过只对振动信号时域波形图进行分析还无法得到故障类型，这就要求对该信号继续深入分析，通过提升小波算法分析振动信号的特征并确定故障类型。共选择3种不同的提升小波方法对故障振动信号实施降噪处理，得到图7所示的信号时域波形。

图6 保持架故障信号时域图

图7 降噪后信号时域波形图

由图7可知，按照阈值设定的方法对故障振动信号实施降噪处理可以获得良好的效果，同时还可以清晰地反馈故障振动信号冲击幅值改变情况。从高频分量中能够明显分辨出齿轮箱保持架的故障信息，同时还可以清楚地看到振动信号冲击幅值明显减小。

4 结束语

本文针对旋转机械多故障难以诊断问题，提出了CMF-EEMD方法。通过添加不同的白噪声幅值，不仅克服了EMD的模态混叠现象，也提高了EEMD分解的精度；通过多载波频率仿真信号验证了该方法的可靠性；通过人为制造故障，在强载荷作用下，成功提取了故障特征。本文的研究给强背景噪声环境下旋转机械多故障共存的故障特征识别提供了一种新方法。