覆盖型岩溶塌陷动态演化数值模型研究

熊启华，高 旭，徐 庆，王芮琼，李祖春，陶 良

(1.湖北省地质环境总站，湖北 武汉 430039;2.中国地质大学(武汉)工程学院，湖北 武汉 430074;3.武汉市测绘研究院，湖北 武汉 430022)

覆盖型岩溶塌陷具有表观突发性和内部渐进性的特点，塌陷的发生是在覆盖层内土洞逐渐演化扩展至极限尺寸后，顶板强度不足以支撑其自重而突然失稳垮塌。因此，预测不同水动力环境下岩溶覆盖层土洞的发育规模和极限规模尺寸对于评价覆盖层稳定性意义重大。然而受制于土洞发育的隐蔽性和物探解译的多解性，直接通过技术手段查明土洞发育尺寸的难度较大或精度不高。鉴于此，从土洞发育物理力学机理出发来建立一种定量预测土洞发育规模和稳定性评价的数值模型(即覆盖型岩溶塌陷动态演化数值模型)并加以验证是本文的研究目标。

目前，以地下水变动为主要诱发因素的岩溶覆盖层中土洞发育的机理主要有潜蚀论和真空吸蚀论两种[1]。潜蚀论认为在岩溶溶隙开口附近的水力梯度超过覆盖层土体临界水力梯度而发生潜蚀或剥蚀，形成土洞并逐渐扩展；真空吸蚀论认为地下水水位在覆盖层与溶腔开口交界处上下波动或快速抽吸岩溶水形成负压而使土层剥蚀扩洞。

而目前针对覆盖型岩溶塌陷机理的研究方法主要有解析法、物理模型试验法和数值模拟法。其中，解析法多是基于普氏平衡拱理论探索临界土洞的规模大小[2]或采用极限平衡理论分析给定几何尺寸下土洞顶板的稳定性状态[3]。虽然利用物理模型试验方法来研究覆盖型岩溶塌陷机理的学者较多[4-5]，但定量研究土洞动态发育特征的物理模型试验较少，仅见有：吴庆华等[6]采用恒压取样技术获取岩溶塌陷物理模型试验过程中砂土漏失质量，用来定量评估土洞的发育过程；张少波等[7]通过在物理模型土层中间隔一定距离布设孔隙水压力自动监测点，通过监测土洞发育过程中造成的不同位置处孔隙水压力变化的差异来判定土洞的发育阶段。然而，目前物理模型试验很难判定不同发育阶段土洞所对应的稳定性状态。鉴于此，部分学者利用数值模拟手段来评估土洞的稳定性，如：孙金辉[8]结合物理模型试验并基于FLAC3D建立了不同规模尺寸土洞开挖数值模型，探索覆盖层地表沉降和内部应力-应变过程；陈冬琴等[9]建立了岩溶塌陷地下水-力学耦合数值模型，并基于此对土-岩交界处溶洞塌陷进行了地下水水位升降及降雨入渗作用对岩溶塌陷的影响分析。

上述研究基本都是人为设定土洞尺寸再进行数值模拟，并不是自适应的土洞扩展演化过程。鉴于此，本文以潜蚀论为基本出发点，建立了覆盖型岩溶塌陷动态演化数值模型，并用于土洞发育规模预测。首先，以武汉市烽火村岩溶塌陷实例为分析对象，概化其岩溶塌陷工程地质模型，并建立渗流-力学单向耦合控制方程，同时结合土洞剥蚀判据编制覆盖型岩溶塌陷动态演化计算程序；然后，基于此程序预测在不同水动力环境条件下覆盖层中潜在土洞的发育规模，并提出临界致塌水位差和极限土洞尺寸；最后，基于普氏平衡拱理论对预测结果进行验证分析。

1 覆盖型岩溶塌陷动态演化数值模型

1.1 覆盖型岩溶塌陷工程地质模型概化

图1 烽火村覆盖型岩溶塌陷地质剖面图

据此，将烽火村覆盖型岩溶塌陷概化为如图2所示的工程地质模型，其覆盖层总厚度为30 m，黏砂层厚度比为1∶5，模型尺寸为100 m×35 m，其中基岩厚度为5 m，网格剖分为1 m×1 m单元。

图2 烽火村覆盖型岩溶塌陷工程地质概化模型

该岩溶塌陷是长期人工抽取地下水诱发的，定性分析认为覆盖层中孔隙水位常常高于岩溶水位，导致存在孔隙水向岩溶水补给渗流过程中当水力梯度超过某一临界值时出现砂土潜蚀或剥蚀现象。土洞剥蚀类似地下工程开挖卸荷，必然伴随着洞周应力重分布、地表沉降、塑性区发展等一系列力学响应；加之，地下水渗流场的存在不仅是土洞剥蚀的直接动力源，同时也造成对土洞的渗流荷载。因此，在渗流荷载与卸荷荷载联合作用下，当土洞的应力、应变超过其极限状态时则产生岩溶塌陷。

鉴于此，覆盖型岩溶塌陷动态演化数值模型就是建立起能够描述地下水流场中土洞扩展的渗流-力学单向耦合控制方程(此处单向耦合是指岩土体的应力-应变不改变其渗透性质，而只有渗透力的单方面力学作用)，且通过土洞剥蚀判据和土洞应力-应变状态来控制土洞扩展演化进程。下面阐述渗流-力学单向耦合控制方程式及其所用参数和边界条件，以及土洞动态演化的计算流程。

1.2 渗流-力学单向耦合控制方程式及其边界条件

数值模型不考虑剥离后土体的运动状态，且假定剥离前土洞岩土体介质处于小变形状态，故采用二维等效连续介质有限元数值模型模拟基岩和覆盖层地下水流场，以及在地下水渗流作用下土洞剥蚀过程中变形和塑性区的发展过程，故模型的力平衡方程如下：

(1)

(2)

式中：γg为岩土层重度(kN/m3)；VA为被剥蚀单元体积(m3)；[B]为关于应变与位移之间关系的几何矩阵；[N]为典型四节点等参单元形函数。

另一方面，作用于非剥蚀单元节点上的渗透力则是与地下水渗流梯度有关[10]，其渗流荷载的数学表达式为

(3)

式中：γw为地下水的单位重度(kN/m3)，取10 kN/m3；Ω为土洞外渗流区域；H表示总水头(m)，其与压力水头p(m)的关系式为H=Z+p，其中Z表示节点竖向高度(m)。

一方面，考虑到研究区覆盖层内土洞埋深一般在30 m以浅，所处围压环境较小，岩土体材料一般不会出现应变硬化特性，但由于采用岩土体应变软化弹塑性本构模型来描述其达到峰值强度后应力-应变关系的参数难以测定，故综合考虑采用岩土体屈服极限不随应力状态改变而改变的理想弹塑性模型来描述土洞的非线性应力-应变过程；另一方面，考虑到岩土体材料属于摩擦型材料，故采用最常用的Mohr-Coulomb屈服准则。本模型不考虑岩土体塑性变形过程中的剪胀效应，因此采用非关联流动法则来描述单元进入塑性状态后的应变规律，其塑性势函数中的剪胀角参数设为0。

为了展示土洞演化中存在的塑性区分布情况，定义塑性应变不变量为[11]

(4)

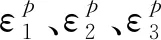
考虑到孔隙水位以上土层处于非饱和状态，采用变饱和地下水稳定流控制方程来统一描述整个模型中的渗流场：

(5)

式中:p为压力水头(m)；K(p)为岩土层渗透系数(m/d)，对处于饱和状态(p≥0)的岩土层渗透系数取饱和渗透系数，而对处于孔隙水位以上的非饱和岩土层渗透系数则是压力水头的函数，采用最简单的指数型模型表征为

(6)

式中：Ks为岩土层饱和渗透系数(m/d)；αm为孔隙尺寸分布参数(m-1)。

如图2所示，模型力学边界条件设置为左右边界约束水平位移；而底边界同时约束水平和垂直位移；上边界为自由边界。对于水力边界条件，BC段和DE段设置为总水头H1的定水头边界，代表弱承压的孔隙含水层水位；而AB段、AF段、EF段则设置为代表岩溶水位H2的可变定水头边界，即通过同时调整此三段水头来模拟不同的岩溶水动力环境条件；上边界CD段为零流量边界。

据文献[14]可知，能使类似地层土洞出现剥蚀的临界水力梯度(Ibs)取0.5。通过归纳总结相关文献[15]和《武汉市岩溶塌陷调查子项目成果报告》(编号为1212011220189)确定数值模型所用的渗流和力学计算参数，见表1。

表1 数值模型所用的计算参数

上述公式(5)和(6)所代表的渗流场计算则采用变饱和渗流计算程序vsaft2[16]，得出的水头场根据公式(3)计算出作用在节点上的渗透荷载;然后修改文献[17]中第6.4.5节关于组装节点荷载的子程序LOADPS，将渗透荷载和根据公式(2)计算的土洞剥蚀后卸荷荷载组装成总体荷载矢量；最后由文献[17]提供的非线性弹塑性力学计算程序完成计算。

1.3 土洞演化的计算流程

结合岩溶塌陷工程地质概化模型和渗流-应力单向耦合控制方程，可得到土洞动态演化计算流程(见图3)如下：

图3 土洞动态演化的计算流程

(1) 首先，在溶隙开口部位设置一个几何较小的初始土洞，土洞和溶隙内都填充扰动土，而其他各岩土层都按原生地层几何参数赋值。

(2) 在给定的水力边界条件下按照公式(5)求解渗流场，进而得到水力梯度空间分布。一方面，利用该水力梯度空间分布情况来搜索出与土洞紧邻的土层单元中水力梯度I大于或等于临界水力梯度Ibs(即I≥Ibs)的单元，并纳入到下一次渗流场计算中的扰动土单元，同时作为下一次应力场计算的剥蚀单元；另一方面，基于水力梯度空间分布，即可根据公式(3)计算出作用在模型中每个单元的渗透力，并结合土洞单元剥蚀卸荷作用，计算模型的力学响应(包括变形和塑性区等)。

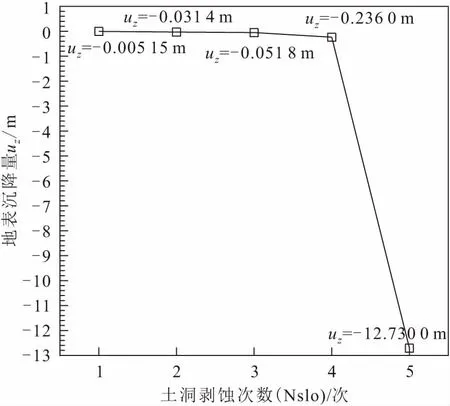
(3) 根据新形成的土洞再次进行渗流场和应力场的计算，并重复上述步骤，直到满足如下两个终止条件之一：①紧邻土洞的土层单元水力梯度I全都小于临界水力梯度Ibs(即I

2 不同水动力环境下土洞发育规模预测

本文设置模型孔隙水位H1=32 m用于模拟覆盖层的承压水环境且保持不变，而通过降低岩溶水位H2用于模拟孔隙水位与岩溶水位之差ΔH(见图2)稳定在4 m、6 m、8 m、10 m、12 m、14 m、16 m这七种水动力环境，借以探索不同水位差环境持续作用下覆盖层中潜在的稳定土洞发育规模，以及临界致塌水位差和极限土洞规模。

先分析在ΔH=16 m水动力环境持续作用下土洞逐渐扩展过程中模型渗流场、水力梯度、塑性区以及位移场情况。设置地表沉降监测点位于如图2所示蓝色圆点处，并记录在ΔH=16 m水动力环境持续作用下土洞演化过程中地表监测沉降量，见图4。

图4 ΔH=16 m水动力环境持续作用下土洞演化过程中地表监测沉降量(uz)变化曲线

由图4可见，土洞在剥蚀次数(Nslo)从第4次到第5次时，地表监测沉降量出现剧烈突变，说明在第5次土洞剥蚀后覆盖层出现地面塌陷，而第4次土洞剥蚀后形成的土洞接近极限土洞规模大小。鉴于此，本次只展示前4次土洞演化过程中渗流场和力学响应的变化规律,见图5和图6。

由图5可见：土洞演化过程中渗流场的流线主要向土洞中心汇聚，孔隙水向岩溶水补给，随着土洞逐渐扩展演化，越靠近土洞总水头越低[见图5(a)]；土洞演化过程中水力梯度小于临界水力梯度的范围基本不变(即覆盖层中半圆形红色圈定范围)，说明孔隙水位与岩溶水位之差ΔH一旦固定时，土洞扩展范围也基本确定[见图5(b)]。

图5 ΔH=16 m水动力环境持续作用下土洞演化过程中渗流场和水力梯度的变化规律

由图6可以进一步地直观看出：土洞剥蚀后规模大小由最初的洞高1 m和洞宽3 m演变为洞高5 m和洞宽9 m的极限土洞规模，且随着土洞的扩展演化，土洞周围砂土层中塑性区范围和塑性应变量逐渐增大，直到第4次剥蚀后塑性区扩展到砂土层顶部，即代表此时覆盖层出现大面积塑性破坏[见图6(a)]；初始土洞形成后无论地表还是土洞周围位移都较小，而当土洞逐渐扩展，地表和土洞周边位移都显著增大[见图6(b)]，但从图6(b)中代表位移矢量方向的红色箭头线可知，地表主要以水平位移为主，而土洞中心线附近则以垂直位移为主,这能够较好地解释实际塌陷坑周边出现拉裂缝且塌陷坑中心竖直沉降量最大这一现象。

图6 ΔH=16 m水动力环境持续作用下土洞演化过程中塑性区和位移场的变化规律

以上仅从ΔH=16 m水动力环境条件下土洞演化过程及塌陷机理进行阐述，而在不同水位差水动力环境下土洞演化过程如图7所示，图中仅展示了模型x=40 m到x=60 m、z=3 m到z=13 m的局部塑性区发展情况[见图7(a)至图7(l)]及其对应稳定土洞规模和地表监测沉降曲线[见图7(m)]。其中,w代表土洞洞宽(m);h代表土洞洞高(m);uz代表地表中心监测沉降量(m)。

图7 不同水位差水动力环境下土洞演化过程中塑性区及其对应稳定土洞规模和地表监测沉降曲线

由图7(a)至图7(l)可见:当水位差ΔH在4～8 m时，土洞保持初始土洞大小并未扩展，说明在此水动力环境下砂性土层水力梯度I超过临界水力梯度(Ibs=0.5)的范围较小，没有土层单元被剥蚀；而当水位差ΔH稳定在10 m时，土洞发生剥蚀而扩展至洞高3 m和洞宽5 m，塑性变形也有所增加;同样地，当水位差ΔH稳定在12 m和14 m时，土洞剥蚀后形成的稳定土洞规模相应变大；当水位差ΔH为14 m水动力环境下土洞最终并未出现塌陷现象，即没有出现类似如图4所示的地表监测沉降量突变或计算不收敛的情况，这说明水位差ΔH需要达到16 m左右(即塌陷临界水位差为16 m),才可能出现最终塌陷现象。

由图7(m)可以看出：土洞洞宽曲线斜率总体大于洞高曲线斜率，说明土洞演化过程中洞宽扩展速率大于洞高扩展速率；地表监测沉降量随着水位差ΔH增加而增加，地表沉降速率大致也可分为三个阶段，即①当ΔH=4～8 m时地表沉降速率最小，②当ΔH=8～12 m时地表沉降速率居中，③当ΔH=12～16 m时地表沉降速率最大，说明地表沉降速率会随水位差所处范围不同而不同，水位差越大，地表沉降速率越大。

3 土洞预测结果验证

(7)

本文基于覆盖型岩溶塌陷动态演化数值模型预测的土洞极限洞高相对普氏平衡拱理论求解的土洞极限洞高偏小，其原因在于普氏平衡拱理论的致塌力只有自重作用，而本文数值模型中考虑了渗透力和自重的联合作用，使得在相对较小的土洞规模下仍会产生失稳破坏。

4 结 论

本文结合弹塑性理论和变饱和渗流理论，以临界水力梯度为土洞剥蚀判据，提出了覆盖型岩溶塌陷动态演化数值模型，探索了在不同孔隙水位与岩溶水位之差水动力环境下覆盖层中潜在土洞的发育规模，并加以验证，得出如下结论：

(1) 在孔隙水位与岩溶水位之差ΔH小于8 m的水动力环境持续作用下，土洞将保持较小规模而不会进一步扩展;而当水位差ΔH超过8 m后将存在土洞剥蚀现象，且水位差越大，最终形成的土洞规模越大。

(2) 当水位差ΔH达到16 m的临界水位差时，土洞将逐步剥蚀至产生塌陷，其极限土洞规模为洞高5 m和洞宽9 m，比基于普氏平衡拱理论预测的土洞规模偏小，其误差为15%。

(3) 覆盖型岩溶塌陷动态演化数值模型能够较好地模拟土洞扩展演化及其失稳塌陷过程，可定量解释覆盖型岩溶塌陷的潜蚀—渗压—自重致塌模式。