数形结合思想在初中数学教学中的作用

江苏省南通市北城中学 陈 娟

在过去的初中数学教学当中，教师往往将更多的时间花在对学生的知识讲授上，而对于学习方法及数学思想的涉及较少。故而，一些学生能够通过学习探索找到更适合自己的学习方法，而另一些学生没有找到高效的学习方法，因此在进行数学学习时遇到了很多困难。这会让这些学生丧失学习的信心和动力，甚至害怕数学。因此，帮助学生掌握高效数学学习法是很有必要的。在数学研究方法当中，数形结合思想是一个很重要的思想，也是解题的有力工具，它能够将晦涩难懂的抽象内容更直观地展现出来，有助于学生理解数学知识。

一、通过数形结合解决概念理解的难题

在数学这门逻辑思维较强的学科当中，概念的教学一直都是其中的难点。与小学数学比起来，初中的数学概念加入了许多的抽象成分。而数学学习当中的概念不能仅靠学生死记硬背，更需要学生切实理解并正确使用。因此，如何解决学生学习概念这一难题，给初中教师提出了新的挑战。数形结合的思想是一种把抽象化为形象的数学思考方法，它通过将条件和关系呈现在图形上来启发学生思维，让学生直观地去理解数学内容。 除此之外，图形往往比文字更加容易被学生记忆，因此，通过数形结合的方式学习到的概念知识，往往能给学生留下更深刻的印象，教师在概念的教学当中要利用好这个方法。例如在学习“平方根”这个内容时，由于正方形面积是边长的平方，因此，教师可以借助正方形这个图形，通过正方形面积的平方根是其边长来帮助学生理解平方根的概念。由于一对相反数的平方是相同的，而正方形的边长只能是正数，因此，我们将一个数开平方后得到的正数称为算术平方根。而开方操作是针对正方形的面积，所以正方形的面积也被称为被开方数。 通过数形结合的方法来解决概念理解当中的难题，能够让学生对知识点有更深的印象，达到教学目的。

二、借助数形结合解决条件复杂的数学问题

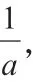
三、用数形结合处理函数问题

函数问题是初中出现的众多新知识之一。 抽象是函数问题的一大特点。不同于上面提到的条件复杂而计算简单的题型，函数问题通常有较为简练的题干，并且计算也往往比较简单，但函数仍是初中数学学习当中的一大难题。这是因为函数需要学生有较强的数学分析能力以及灵活的思维。在处理与函数有关的问题时，数与形的结合恰恰是帮助学生打开思维的好途径。例如函数题目：“反比例函数y=图像的其中一支位于第一象限。问：（1）图像的另一支位于哪个象限？常数m 的取值范围是什么？（2）在这个函数上任取点 A（x1，y1）和点 B（x2，y2），如果 x1大于 x2，那么，y1和y2有怎样的大小关系？”这是一道比较简单的反比例函数题，如果让数学学得比较好，并且能力比较强的学生来做这道题，或许可以不借助图像就完成习题。但对于数学基础不是特别好，或是抽象思维能力不够强的学生来说，在不借助图形的情况下完成这道题目是很容易出错的。但如果依据题目的条件顺序，将已知条件标记在图形上，相信绝大多数学生都不会出现错误。

数学这门学科具有自己的特殊性，不同学生的最适学习方法是不一样的，适合某些学生的方法也许并不适合另一些学生。因此，学生在学习数学时要能够找到自己的学习节奏。但大多数数学思想，却是对所有学生都适用的，只是有些学生没有完全掌握这些思想故而不能熟练运用，也自然体会不到使用这些思想的妙处。教师需要助学生打破壁垒，更进一步。