双圈磁钢飞轮电机的设计及优化*

殷 明，王 森，陶侃凯，聂 周，裴 堃，刘 凯

(1.广东电网有限责任公司机巡作业中心·广州·510180；2.上海航天控制技术研究所·上海·201109；3.东南大学 电气工程学院·南京·210096)

0 引 言

反作用飞轮系统是卫星等航天器实现姿态调节的执行机构，该系统具有体积小、质量小、精度高、可靠性高和寿命长等特点。飞轮电机是航天器姿态控制系统中的关键部件，其性能直接影响航天器的控制精度、稳定性、系统功耗及运行效率[1]。典型的飞轮结构有内转子结构、外转子结构和分装式结构[2]。

飞轮电机的理想气隙磁密波形为方波，波形质量好坏对控制效果有很大影响，实际运行中，常规飞轮电机产生的气隙磁密波形不是理想方波，而是梯形波。如果平顶波宽度不够，会产生较大的转矩脉动，影响电机的控制精度[3]。另外气隙磁密幅值大小对电机损耗也有影响。为了改善常规飞轮电机的气隙磁密波形的质量，提高电机运行性能，本文在常规飞轮电机的基础之上提出了一种双圈磁钢飞轮电机的结构，首先对双圈磁钢飞轮电机本体进行电磁设计，其次利用有限元软件对该电机的磁极对数和极弧系数进行优化，最后与常规飞轮电机进行电磁转矩和运行损耗进行比较。

1 飞轮电机的结构设计

常规飞轮电机的永磁体粘贴在转子铁心内壁，当转子转动时，电机内的磁场呈周期变化[4]。当电机高速运行时，电机内部的温度会升高[5]。因此，电机材料必须具有良好的热稳定性和耐高温特性[6]。本文提出的双圈磁钢永磁无刷直流电机，转子部分的内轭外壁和外轭内壁都粘贴永磁磁钢，定子采用无铁心结构，置于内外转子间气隙中，内外转子铁心及磁钢轴向长度均相同。双圈磁钢飞轮电机结构的二维剖面图如图1所示。表1所示是电机的具体设计指标。飞轮电机的转子呈空心杯结构，定子材料由不导磁的环氧树脂材料浇注构成，电机的绕组嵌在环氧树脂材料之内。

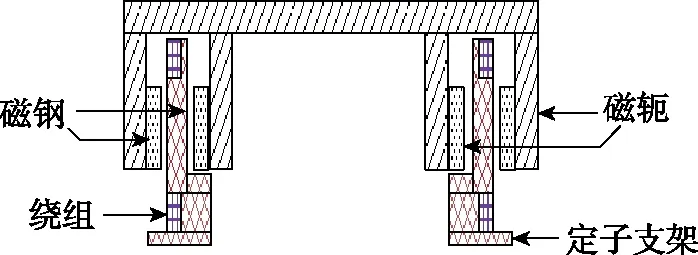
图1 飞轮电机结构剖面图

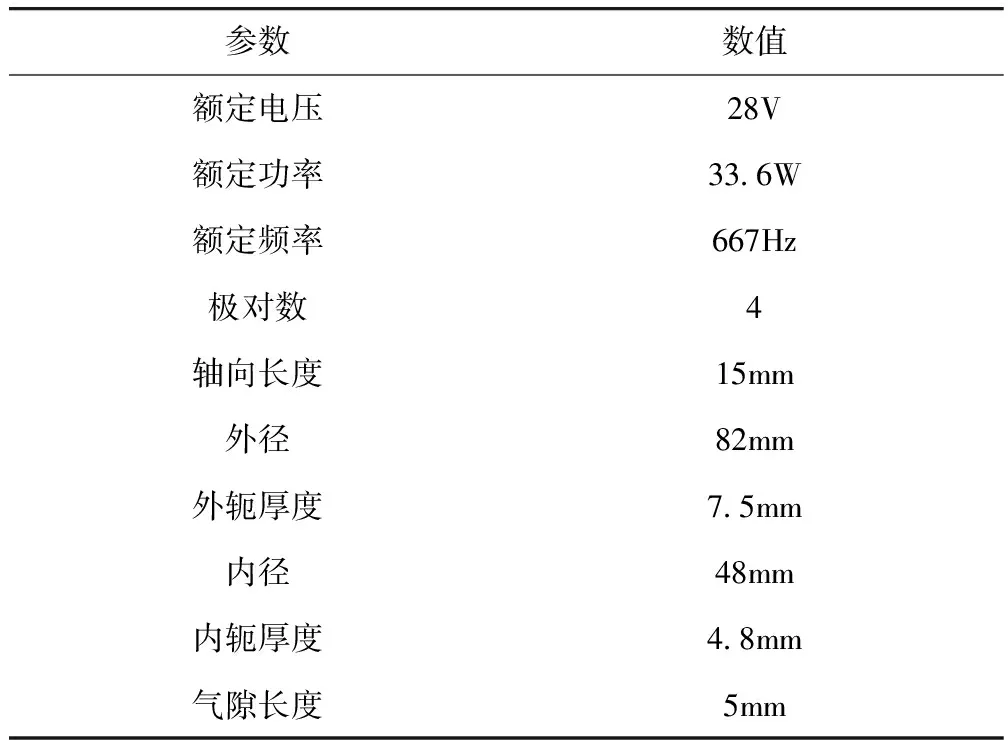
表1 飞轮电机的设计指标

根据上述设计指标，可以确定电机绕组的匝数，给定电压为28 V，功率管导通压降为0.3 V，导体有效长度L=10 mm，计算极弧系数αi=0.9；最高转速nmax=10000(r/min)。

φδ=BδαiτL=1.0723×10-4(Wb)

式中：φδ为磁通量；αi为计算极弧系数；τ为极距；L为导体有效长度。

线圈匝数：

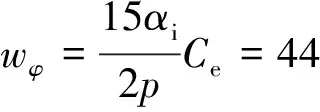
式中：wφ为线圈匝数；Ce为反电势系数；p为极对数。

转矩系数：

取电流：I=1.2 A则

Temax=KTI=36(mN·m)

满足最大输出力矩要求。

2 电机磁极的优化

2.1 磁极对数的优化

双圈磁钢飞轮电机的磁极对数会直接影响电机性能，磁极对数越多，电机运行频率越高，电子器件换向损耗越大，另一方面，磁极对数增加时，线圈元件空间变小，飞轮电机在安装霍尔传感器时就会出现一定的困难，另外电机磁极对数增多，电机漏磁会增大[7-9]。电机的运行性能会变差，磁极对数过小时，在输出转矩不变的前提下，绕组匝数会增大，电机空间利用率会下降[10]。因此选择磁极数目的时候要综合考虑多方面的因素，最终做出选择。本文针对双圈磁钢飞轮电机的电磁设计，先做出以下假设:

(1)飞轮电机定转子结构的尺寸不变；

(2)飞轮电机磁钢采用平行充磁的方式，磁极间隔为0。

首先利用二维有限元软件分析磁通密度在飞轮电机中的分布，求解不同极对数(3对极到8对极)下的气隙磁密波形，为确保磁通经过电机转子铁轭时不发生饱和，飞轮电机的铁心厚度选取足够大的厚度。由图2可得，不同的磁极对数，气隙磁通的径向分量和波形宽度有所不同。当磁极对数增加时，气隙磁密幅值会增大，但是磁极过多时，磁极间的漏磁会增大，气隙磁密平顶波的宽度就会减小。综合考虑气隙磁通的幅值和平顶宽度，最后确定飞轮电机最佳磁极对数为4。

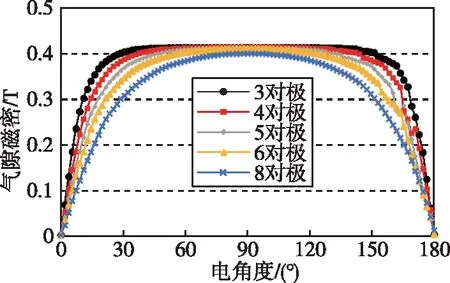
图2 不同磁极对数下的气隙磁密波形

2.2 磁极极弧系数的优化

当飞轮电机旋转时，转子铁轭中会出现漏磁。当飞轮转速不高，电机电频率不大时，漏磁引起的壳体等部件的涡流损失较小。然而，由于漏磁通的谐波含量大，由漏磁引起的涡流效应不可被忽略。因此，有必要采取措施减少飞轮电机转子的漏磁。图3(a)所示，当飞轮电机的磁极间隔为0°，即极弧系数为1时，磁力线直接闭合在磁极的连接处，磁力线经过的磁阻很小。磁极间的漏磁较大。图3(b)的磁极间隔大于0°，即极弧系数小于1时，磁极之间的磁阻会增加，电机漏磁也相应减小。

建立飞轮电机不同磁极间隔的有限元模型，磁极分别间隔0°、2°、4°、6°和8°，随着相邻磁极间距的增加，飞轮电机外转子的漏磁显著减小，如图4所示飞轮电机铁心气隙磁密的曲线，可以看出，漏磁减小的速率随着磁极间隔的增加而减小。当磁极间隔逐渐增大时，气隙磁密波形幅值会逐渐减小，平顶波宽度会缩减。图4是不同磁极间隔下的外铁心磁密波形。图5是不同磁极间隔下的气隙磁密波形。在保证电机运行性能不变且减小飞轮转子漏磁的情况下，磁极间隔选取4°最为合适。

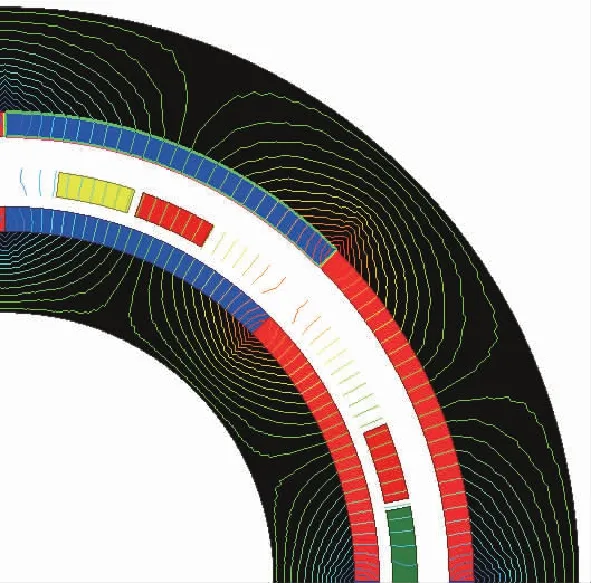
(a)极弧系数为1

图4 不同磁极间隔下转子的外铁心磁密

图5 不同磁极间隔下的气隙磁密

2.3 磁钢厚度的确定

飞轮电机的磁钢厚度是一个重要的参数，在设计中必须考虑。图6中所示是飞轮电机的关键尺寸，由于内外磁轭之间的距离保持不变，因此磁钢厚度h和空气长度之和间隙δ为常数。当磁钢厚度不变时，气隙长度确定。综合考虑飞轮电机的制造工艺和稳定运行，需要在定子骨架和转子之间留出一定的间隙。因此，骨架和磁钢之间的距离h1具有最小值。

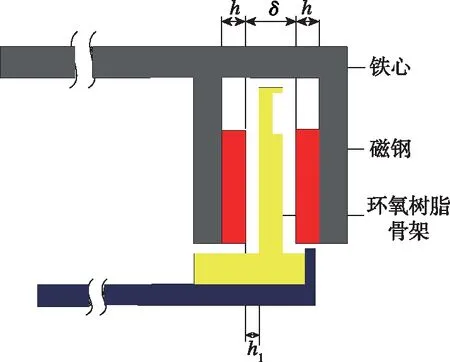
图6 飞轮电机的关键尺寸

考虑到定子骨架的支撑强度，定子骨架的厚度有一个最小值。因此，磁体厚度h和绕组厚度之间的距离具有固定的最大值。电压一定时，磁钢厚度增大，电机的气隙磁通密度增大，绕组匝数减小，相反磁钢厚度减小，绕组匝数增大，因此，在一定的磁钢厚度下，绕组电阻必然有最小值。

由于内外转子铁心构成磁通回路中导磁部分，其内部磁场饱和程度对气隙磁密有很大影响。铁心内部饱和程度一方面跟铁心软磁材料选择有关，另一方面与其径向厚度有关。当转子铁心厚度比较小，铁心内部磁密饱和程度就会较高，有效磁通和气隙磁密的幅值也就较小[11]。随着铁心厚度的增加，铁心内部磁通增大，气隙磁密幅值也线性增大，当铁心达到一定厚度时，永磁体产生的磁通已经可以完全通过气隙，铁心此时处于非饱和状态。当铁心厚度再增加时，气隙磁密幅值随转子铁心厚度增加不再增加，从而达到稳定状态。因此，电机铁心的厚度应设置在饱和临界点附近，使永磁体产生的磁能充分发挥效用。由图7所示，飞轮电机的转子铁轭厚度选在4 mm。

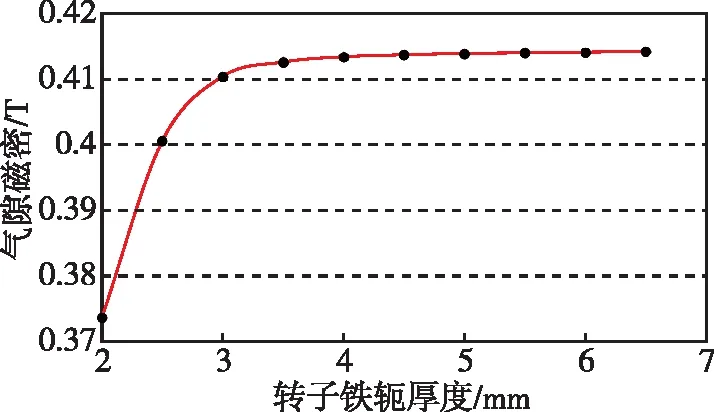
图7 气隙磁密幅值随转子铁心变化图

3 与常规飞轮电机的性能对比

3.1 电磁转矩的比较

电磁转矩是电机重要性能指标，计算电磁力和电磁转矩的基本方法有麦克斯韦张量法和虚位移法。目前麦克斯韦应力张量法被更多地用来计算电磁转矩[12]。

在Ansoft Maxwell中可以用麦克斯韦张量法来求解电机力矩。其具体步骤如下：

(1)给模型中要计算力的部分加面域，通常给飞轮电机气隙处——磁极间包含绕组的真空域加Maxwell面标志；

(2)计算出力后将结果贮存到这些空气单元中，程序对所有单元进行力和力矩计算。在电机电枢电流为1.2A时，仿真计算得出的常规飞轮电机和双圈磁钢飞轮电机的输出转矩波形如图8和图9所示。

转矩脉动系数为

计算得到常规飞轮电机转矩脉动系数为23%，双圈磁钢飞轮电机转矩脉动系数为5%，由此看出，双圈磁钢飞轮电机的转矩明显减小。

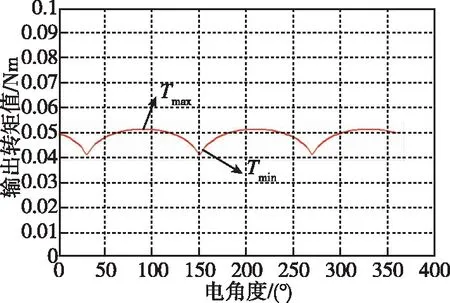
图8 常规飞轮电机输出转矩

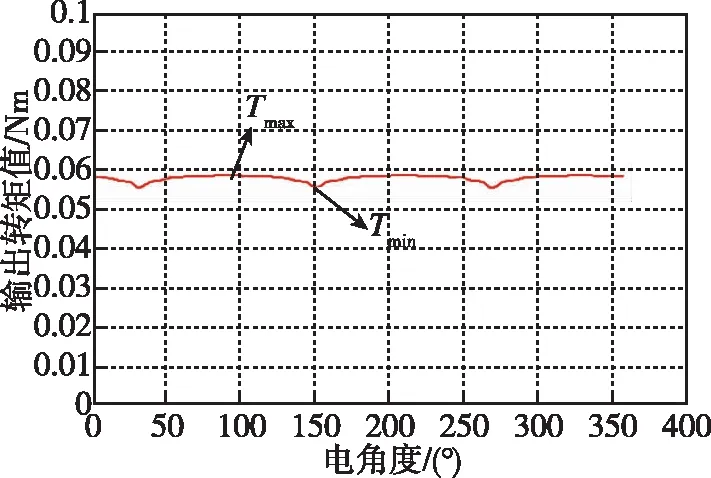
图9 双圈磁钢飞轮电机输出转矩

3.2 电机损耗的比较

飞轮电机的损耗一般分为三个部分，铁心损耗、绕组损耗和磁极损耗，由于本文所研究的飞轮电机电频率较小、导线半径不大，导线和磁极的涡流损耗可以忽略不计，同时电机运行过程中，磁极随铁心一同旋转，因此电机内外轭铁心损耗可以忽略不计。飞轮电机在运行时，电机永磁体与转子之间无相对运动，铁心的涡流损耗基本忽略不计，然而电机的上盖和底座相对于转子静止，因此永磁体端部漏磁有可能在导磁部件中产生涡流损耗[13]。本文研究的飞轮电机是在真空环境下运行，风阻可以忽略不计，因此影响飞轮降速功耗的因素主要为机械摩擦和漏磁产生的旋转损耗，由于双圈磁钢磁场的分布相比常规单层磁钢产生的磁场分布更均匀，理论上双圈磁钢飞轮电机的铁心端部损耗要比常规飞轮电机的损耗小，如图10所示是仿真计算得出的飞轮电机的铁心损耗随电机转速变化图，而其他损耗，两种电机差别可忽略不计，因此总体电机损耗双圈磁钢飞轮电机相比常规飞轮电机运行损耗更小。

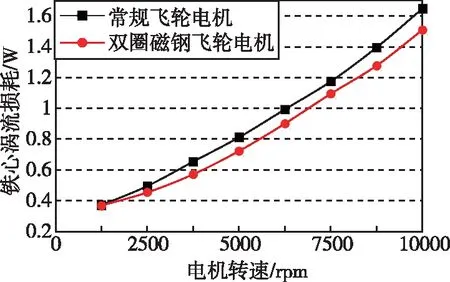
图10 两种飞轮电机铁心端部损耗随转速变化图

4 结 论

根据航天器姿态调节系统中的具体要求，本文在常规飞轮电机的基础上设计了一种双圈磁钢飞轮电机，首先确定了飞轮电机的尺寸和大小。其次在不改变飞轮电机轴向长度和绕组电流密度不变的情况下，当磁极对数选为4对极，气隙磁密波形的质量更好；通过增大磁极间隔，优化电机的极弧系数，可以减少飞轮电机转子的漏磁。最后将双圈磁钢飞轮电机与常规飞轮电机进行了性能对比，结果表明双圈磁钢飞轮电机的转矩波动和损耗更小，电机的运行性能更好。