光纤陀螺零偏温度误差补偿方法分析*

张春梅，刘晓庆

(中国航天科工集团7801研究所·长沙·410205)

0 引 言

作为新型全固态光学陀螺，光纤陀螺已经被广泛应用于海、陆、空等各个领域，并且以其自身独特的优势，即抗冲击、灵敏度高、寿命长、动态范围大、启动时间短的优点，在惯性领域得到了大力发展与应用[1-2]，并向着高精度和超高精度方向不断发展与进步。但由于光纤陀螺的核心部件光纤环对温度极其敏感，只要光纤环周围的温度发生变化就会被光纤陀螺的零偏输出所敏感到，进而产生零偏漂移[3]，严重地限制了光纤陀螺向高精度方向的发展。

为了减小零偏漂移对光纤陀螺的影响，通常的方法是改变光纤环的绕法，使其自身能够对温度进行更有效的自补偿，但这种方法有一定的技术难度[4-6]；另一种方法是对陀螺的零偏输出直接进行软件补偿。在实际应用与学术研究中第二种方法的普遍接受程度较高，且补偿方法简单，不必改变光纤环的初始状态。

李战等的零偏温度补偿因子只有温度，没有反映出温度变化对输出的影响，补偿效果较差[7]；冯卡力等虽然对整段温度补偿进行分段，但补偿因子依然只有温度，且分段情况视陀螺个体的温度特性而定，存在不稳定因素，工程应用不便[8]；赵冰等的零偏补偿模型中只有单点的温度和温度变化率以及它们的交叉项作为补偿因子，一点温度的变化不能充分反映整个陀螺的温度变化形态，且有交叉项的存在不仅增加了应用难度，也没有证明它存在的意义[9]；刘颖等则应用了包括单点温度和两点温度差为因子的补偿模型[10]；杨智杰等则只用了温度差和温度变化率的差作为补偿因子[11]；这些方法都没能全面地体现光纤环的温度真实变化情况，而其他的一些带有智能算法的补偿方式如神经网络和小波变换等方式工程应用困难[12]。

所以基于此情况，本文提出了一种基于光纤环附近多点温度及温度变化率为补偿因子的零偏温度误差补偿模型，根据光纤环的温度敏感特性机理，通过采样光纤环附近多个温度点的温度和温度变化率对光纤陀螺的零偏进行有效补偿，并通过温度实验进行了验证，再与其它单点温度类的温度误差补偿方法的补偿效果进行对比分析，结果表明基于多点温度误差补偿方法的补偿效果更佳。

1 温度对光纤陀螺零偏漂移的影响

环境温度变化和光纤陀螺内部热源是造成光纤陀螺零偏漂移的两个主要方面，当温度发生变化时，光纤环上就会产生热致非互易相移(Shupe误差)，进而光纤陀螺就会发生零偏漂移。光纤陀螺中由于Shupe误差引起的热致旋转速率误差为

(1)

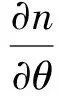
2 多点温度误差补偿模型

为了获取光纤环周围的温度，在光纤环的内侧和外侧分别贴附温度传感器，如图1所示，环内侧和外侧的温度传感器在空间上的位置是一一对应的。考虑到贴附传感器的难度以及可能对光纤环本身造成影响，仅贴附4个温度传感器。

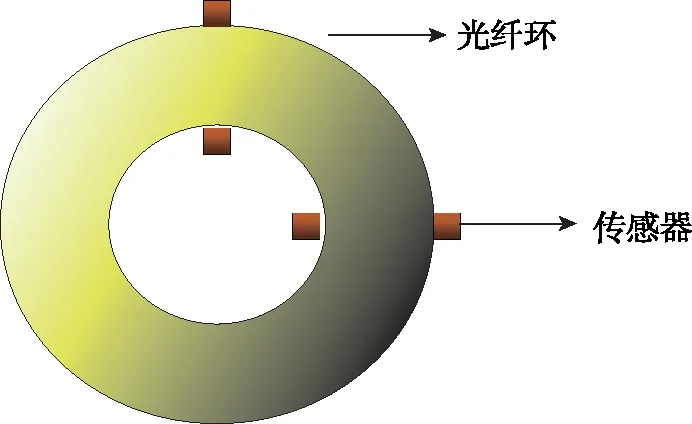
图1 光纤环上温度传感器分布

4个传感器采集的温度分别为T1、T2、T3、T4，则光纤陀螺的温度误差模型为

Y=Y1+Y2+Y3+Y4

(2)

其中，ai,bi,ci,ei,dai,dbi,dci,dei(i=1,2…)对应的是各温度项的系数，dTi/dt(i=1,2…)是光纤环对应温度点处的温度变化率，各项系数由回归分析方法确定。从模型(2)中可以看出，由于多点温度误差补偿模型参考的温度条件增多，更能充分地反映出光纤环受温度效应影响的情况。

3 温度实验与模型验证

根据图1温度传感器的位置对无骨架光纤环(环总长1500 m)进行实际贴附操作，并装成整机光纤陀螺进行温度实验。将光纤陀螺放入高低温箱内，温度条件为：从常温25℃以1 ℃/min的温变速率降到-40℃，保温2 h，再以同样温变速率升温到60℃，同样保温2 h。根据温箱内静态采集的光纤陀螺零偏输出和多路温度数据，利用提出的多点温度误差补偿模型对其进行温度补偿。考虑到实际应用条件以及补偿效果，每个温度点的温度因子为5阶、温度变化率3阶具有最佳补偿效果，再增加阶数已无实际意义，下面的分析皆基于此阶数。

光纤环内侧传感器的温度和其空间位置对应的外侧传感器的温度分布如图2所示，可见，光纤环内外侧的温差还是非常可观的，正是这种存在的温度差异才导致光纤陀螺温度误差的产生。由图3和图4可知，补偿后光纤陀螺的零偏分布比补偿前降低了一个数量级。补偿前后的零偏稳定性和极差对比如表1所示，零偏稳定性降低了两个数量级，极差降低了一个数量级，可见多点温度补偿模型的优势。

为了证明多点温度补偿模型的特殊优势，对比分析了单点、两点、三点温度补偿时光纤陀螺的零偏稳定性和极差，并与四点温度误差补偿模型进行对比(见图5)，类比推理出拥有更多点温度因子情况的误差补偿效果。表2是各点温度补偿后的零偏稳定性和极差对比，从表中可以看出，单点温度误差补偿模型相比多点温度误差补偿模型具有一定的劣势，陀螺全温零偏稳定性和极差都较大，比多点温度误差补偿模型都高一个数量级。图5是多点温度误差补偿模型随温度点数增加的零偏稳定性和极差变化情况，可以发现零偏稳定性和极差都随着温度点数的增加趋于收敛平缓，而在两点温度补偿时较单点有较大幅度的降低，之后趋于平缓，这充分说明了多点温度误差补偿较单点温度补偿的优势。

实际应用中考虑到光纤环贴附传感器的难度以及空间体积占用情况，一般两点或三点温度误差补偿模型便可以满足要求，也不会增加陀螺负荷量，还能大大提高光纤陀螺精度。

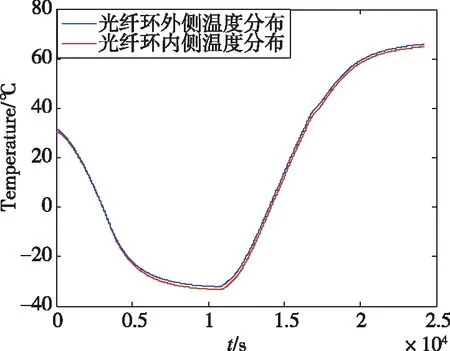
图2 光纤环内外侧温度分布

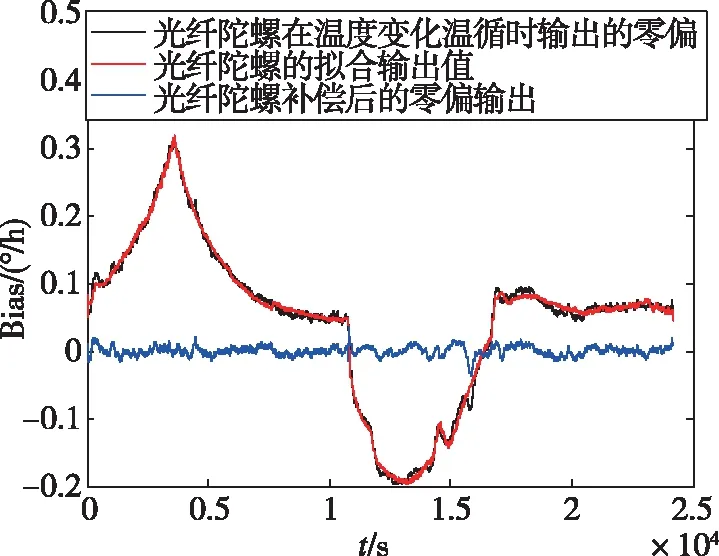
图3 零偏补偿前后对比图

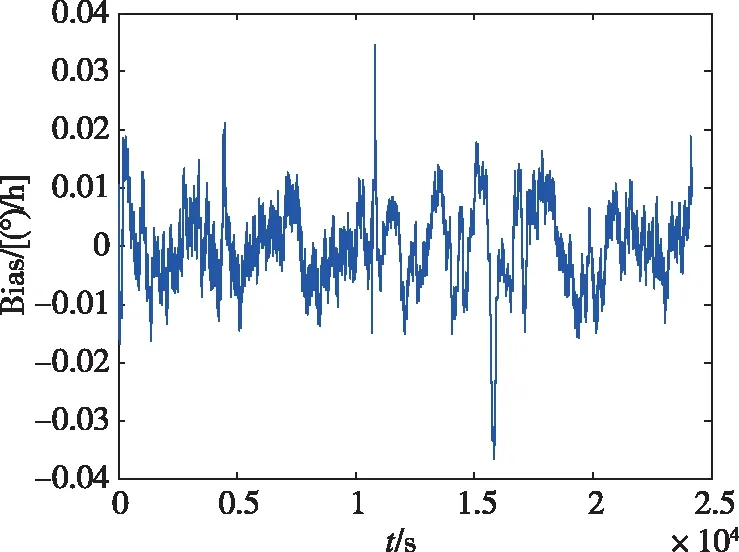
图4 光纤陀螺补偿后零偏分布图

表1 补偿前后零偏稳定性和极差对比

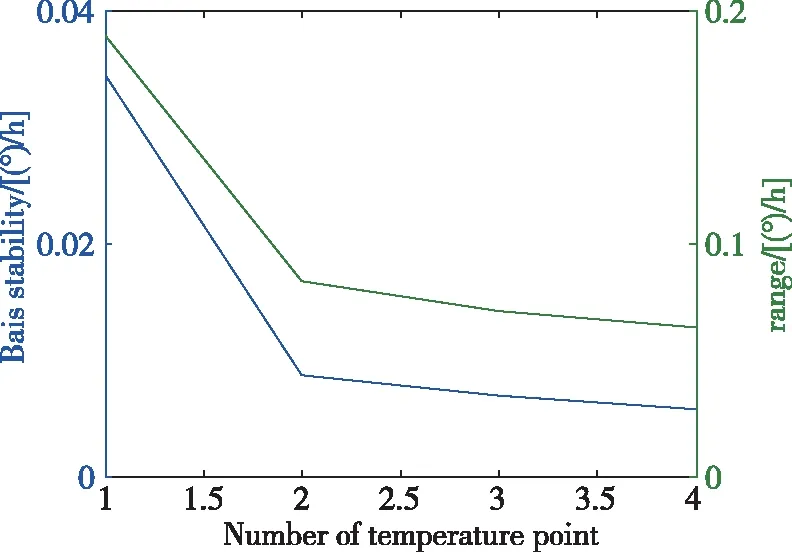
图5 多点温度误差补偿模型随温度点数增加的零偏稳定性和极差变化情况

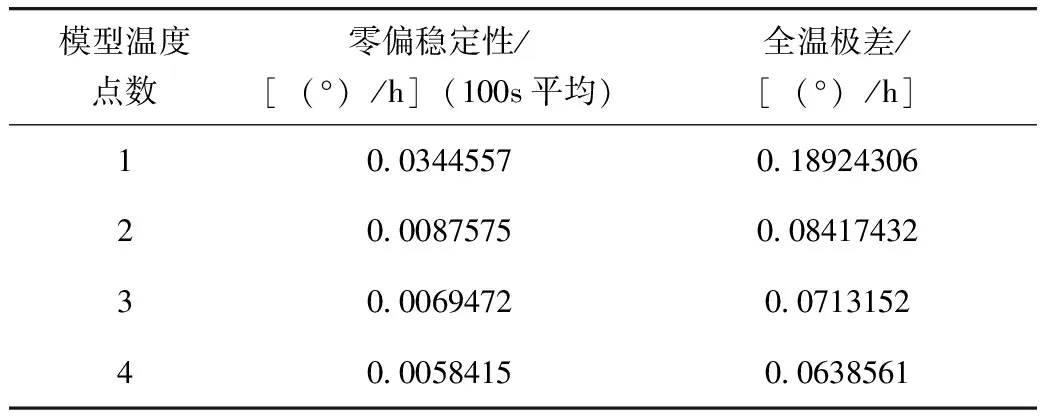
表2 多点温度误差补偿模型的零偏稳定性和极差对比

4 与普通温度误差补偿模型的对比分析

传统的温度误差补偿模型有很多种形式，基本包括：只有温度因子的情况，温度和温度变化率的情况，温度、温度变化率和光纤环内外温度差的情况，温度差和温度差变化率的情况等。其温度误差补偿模型分别如式(3)～(6)所示。

为了与上述多点温度误差补偿模型进行对比，各补偿模型的温度自变量因子的阶数都是5阶，温度变化率和温差以及温差变化率都是3阶，各模型补偿后全温零偏稳定性和极差对比如表3所示。

表3 各模型补偿后全温零偏稳定性和极差对比

M1=anTn+an-1Tn-1+…

(3)

M2=anTn+an-1Tn-1+…+bi(dT/dt)i+

bi-1(dT/dt)i-1+…

(4)

M3=anTn+an-1Tn-1+…+bi(dT/dt)i+

bi-1(dT/dt)i-1+…+cj(Tin-Tout)j+

cj-1(Tin-Tout)j-1+…

(5)

M4=an(Tin-Tout)n+an-1(Tin-Tout)n-1+…+

bi(d(Tin-Tout)/dt)i+bi-1(d(Tin-

Tout)/dt)i-1+…

(6)

从表3中可以看出，无论是哪种补偿模型，不管补偿因子包括多少项，发生怎样的变化，其补偿效果基本都是只能将零偏稳定性降低一个数量级，全温极差仅降低60%左右，而对于多点温度补偿模型，能将全温零偏稳定性降低两个数量级，全温极差降低一个数量级，可见多点温度补偿方案相比较其他应用方案具有极大的优势。而对比一些神经网络、小波变换等一些学术上的智能算法，多点温度补偿方案的工程应用价值更高，而不是停留在学术研究的层面。综上所述，根据光纤环自身温度分布变化情况而设计的多点温度补偿方案具有较高的温度误差补偿效果，且有更高的工程应用价值。

另外光纤陀螺的常温启动时间较长，经试验验证基于多点温度误差补偿方案依然适用于补偿常温启动时间带来的零偏漂移，且补偿效果优于基于单点温度补偿方案，这里就不再详细叙述。

5 结 论

通过分析温度对光纤陀螺光纤环的影响，确定了由于光纤环上温度分布不均使单点温度误差补偿方法根本不能反映出整个光纤环的温度变化趋势，所以提出了一种基于多点温度的误差补偿方案。并建立了多点温度误差补偿模型，通过全温温度试验对多点温度误差补偿模型进行了验证。结果表明基于两点以上温度的补偿模型能将全温零偏稳定性降低2个数量级，全温极差降低1个数量级，而基于单点的温度补偿方案仅能将全温零偏稳定性降低1个数量级，全温极差仅能降低60%左右。且随着补偿模型的温度点数增加，补偿效果越好，且趋于收敛平稳态势，所以一般实际工程应用两点或三点温度补偿模型即可满足。最后通过与其它多种补偿模型进行对比分析，发现多点温度补偿方法既能大大减小温度误差的影响，又能满足工程应用需要，将有更好的应用前景。

最后，由于本次研究只贴附了4个温度传感器，下一步将就4个以上传感器是否能达到更佳效果进行进一步的探究分析。