红外成像系统中带有距离修正的目标能量预测方法*

刘 滨，洪文鹏，王瑞芬，刘建旭，关智聪

(1.上海航天控制技术研究所·上海·201109；2.陆军装备部驻南京地区军事代表局驻上海地区第三军事代表室·上海·201109；3.中国航天科技集团有限公司红外探测技术研发中心·上海·201109)

0 引 言

过去的几十年来，光电对抗技术不断进步[1]，如今的红外成像系统不仅要克服环境中的自然干扰，还要应对目标实施的人工干扰。自然干扰包括强烈的云层辐射、太阳辐射等。人工干扰包括：机载激光武器、红外烟幕、红外诱饵、隐身伪装技术等，这些都对红外成像系统的抗干扰跟踪能力提出了更高的要求[2-4]。

基于红外辐射信息探测技术，红外成像系统能够把物体表面辐射出的红外线转变成人类可直接观察的数字图像[5]，点目标探测系统设计完成时，一般要对系统的能量集中度进行测试和计算，作为评价系统性能的依据，随着光学制导导弹控制精度的提高，当目标被遮挡后，不仅对目标形状、大小和位置有预测要求，对目标辐射能量的预测也需要接近实际值[6-7]。传统的灰度预测方法一直存在灰度快速增长时，预测缓慢的问题，灰度快速增长时无法准确响应，因此对原有的灰度预测方法进行改进，结合了距离信息，建立状态方程，将目标能量及其导数作为状态方程自变量，并利用弹目距离得到状态转移矩阵，用以辅助修正目标灰度，为目标灰度预测提供参考和理论依据[8]，通过和其他传统方法的对比得出该方法具有更高的精度。

1 数学符号说明

2 改进的灰度预测方法

将弹目相对距离引入到灰度预测算法中，以提高目标识别的准确率，算法实现上采用2阶状态向量的Kalman滤波算法，该算法建立在两个假设上：

假设一：整个估计过程中，目标自身的能量无明显突变，对应于目标能量光滑；

假设二：整个估计过程中，统计方法造成的能量损失是一个缓慢的变化过程，对应于统计损失光滑。

建立基本的状态方程

(1)

由于实际系统受采样周期的限制，将上述方程离散化，离散化后的状态方程为

(2)

(3)

测量噪声V(k)为高斯白噪声，其

(4)

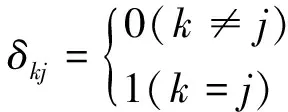
3 仿真分析

结合两种实际的红外成像系统采集到的数据，运用不同的预测方法进行仿真，结果如下。

3.1 改进的灰度预测方法

在没有干扰态时该方法在对灰度进行滤波，滤波效果明显，由于灰度较大是能量本身起伏较大，相对滤波值本身有起伏，由于该方法主要侧重于预测，对滤波的效果不展开讨论。对不同的进入干扰态时间对预测效果进行分析。

(1)2 s后进入干扰状态

假设2 s后进入干扰状态，通过前2 s后的数据预测后面的灰度值，2 s后进干扰且之后全程处于干扰态中，针对两种不同弹道的能量增长的预测效果如图1所示。

图1 灰度预测整体效果(2 s)

由于有效数据较少，此时做预推还是有较明显的误差，弹道1在最大灰度8000的情况下，相对滤波值有1400(最大)的偏差；弹道2在最大灰度150的情况下，相对滤波值有40(最大)的偏差；

(2)4 s后进入干扰状态

假设4 s后进入干扰状态，通过前4 s后的数据预测后6 s的灰度值，4 s后进干扰且之后全程处于干扰态中效果如图2所示。

图2 灰度预测整体效果(4 s)

相较于2s后进入干扰状态，由于使用了前4s的数据进行预推，弹道1在这种情况下的预推精度相对较好，最大灰度8000的情况下，相较滤波值有600(最大)的偏差，弹道2由于整体灰度较小预测，相对的预测误差提升并不明显，在最大灰度150的情况下，相较实际值有34(最大)的偏差。

3.2 三阶状态向量Kalman滤波预测方法[11-13]

由于其他方法无法长时间进行预测，只能进行间隔预测，针对同样的数据采用了传统Kalman滤波算法进行预测，方法为

(5)

其中，H是测量矩阵，Φ是状态转移矩阵。状态一步预测

(6)

状态估计

(7)

滤波增益

K(k)=P(k/k-1)HT[HP(k/k-1)HT+Rk]-1

(8)

一步预测均方误差

P(k/k-1)=ΦP(k-1)ΦT+Qk-1

(9)

估计均方误差

P(k)=[I-K(k)H]P(k/k-1)[I-

K(k)H]T+K(k)RkKT(k)

(10)

卡尔曼滤波是一种最常用的非线性滤波方法[8]，然而卡尔曼滤波的效果与初始估计误差密切相关，过大的初始误差，会造成滤波的发散。由于状态方程和测量方程是近似模型，不满足线性无偏最小方差条件，而是近似最优，所以卡尔曼滤波只是一种次优滤波器[4]，结合该滤波器，进行3 s稳定跟踪然后1 s预测的状态切换，仿真结果如图3所示，对于弹道1该方法与实际的灰度值最大偏差为300左右，对于弹道2该方法与实际的灰度值最大偏差为90左右。

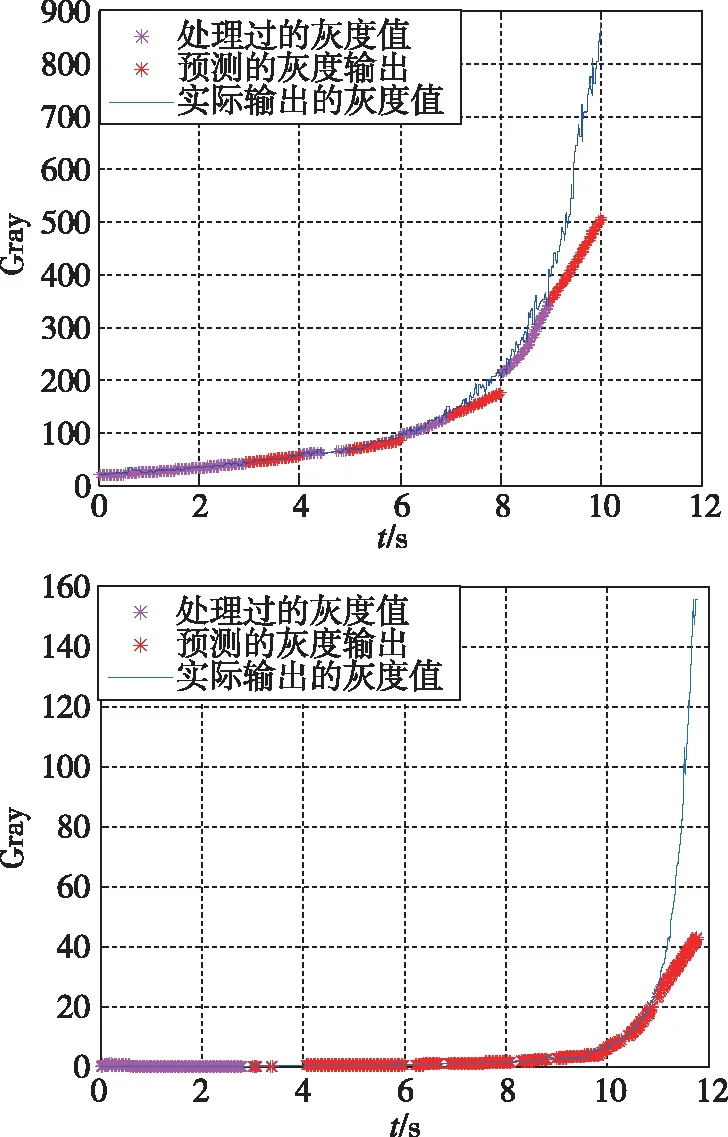
图3 卡尔曼滤波灰度预测整体效果

3.3 α-β-γ滤波预测方法[14]

该方法相对改进方法的优势是其不收敛时间的优化，但系数确定过程难度大。结合该滤波器，进行3 s稳定跟踪然后1 s预测的状态切换，仿真结果如图4所示，对于弹道1该方法与实际的灰度值最大偏差为200左右，对于弹道2该方法与实际的灰度值最大偏差为70左右。

图4 α-β-γ滤波灰度预测整体效果

3.4 结果对比

针对能量预测方法上面给出了几种情况下的仿真结果，下面结合不同弹道的不同投放方式进行仿真，从结果可以看出带有距离修正的目标能量预测方法的预测效果明显优于其他两种方法，但由于弹道2的目标灰度在后期增长更为迅速，所以三种方法对于弹道2的滤波预测效果均不如弹道1，结果整理见表1。

表1 不同方法的对比结果

4 结 论

本文提出的带有距离修正的目标能量预测方法，与三阶状态向量Kalman滤波预测方法、α-β-γ滤波预测方法相比，在弹目距离变化时，灰度预测值与实际值偏差较小，并且由于距离修正的存在，可以在只有初始截获过目标的情况下，借助修正功能准确地预测出目标之后的能量，本文分别对2 s后进干扰态、4 s后进干扰态以及1 s截获1 s干扰交替的3种情况进行了对比分析，并对比了两种传统方法，由表1可以看出误差远小于传统方法的结论，因此该方法可为目标的稳定跟踪提供有效的判据。