基于事件触发的航天器姿态自适应容错控制*
2020-06-02张嘉芮陈弈澄董新蕾王焕杰齐瑞云
张嘉芮,陈弈澄,董新蕾,王焕杰,齐瑞云
(1.南京航空航天大学 自动化学院·南京·211106;2.上海航天控制技术研究所·上海·201109;3.上海市空间智能控制技术重点实验室·上海·201109)
0 引 言
航天器姿态控制系统的目标是实现快速机动、精确指向等预期功能。在整个工作周期中,航天器的姿态控制性能决定了其在轨运行期间的各类技术指标能否实现。一方面,由于星载计算机资源的限制[1],控制器在保证姿态控制性能的前提下,其结构复杂度是一个值得关注的问题。另一方面,在控制系统中,系统稳定性高度依赖于执行机构的正常工作。然而,执行机构在系统运行过程中可能会出现逐步或突然的故障,导致控制效率下降[2],从而降低系统性能甚至导致灾难性事故。TAFAZOLI M[3]指出航天器姿态控制系统故障中执行器故障占34%,因而针对航天器执行器故障的容错控制具有很现实的工程意义。
针对执行器故障的航天器姿态容错控制目前已有大量的研究,CHEN W等[4]通过设计观测器对故障信息进行估计,以完成控制器重构实现容错控制。赵琳等[5]通过设计快速终端滑模面完成了容错控制器设计,虽然提高了系统的收敛速度但是仅能处理部分失效故障且控制器结构较为复杂。韩宇等[6]用误差空间拓扑所得的误差函数描述势能误差,并在此基础上,设计了反步容错控制方法,有效地减少系统响应时间。肖冰等[7]针对执行器故障设计了自适应滑模容错方法,该方法无需故障信息和未知参数,具有较好的鲁棒性和快速性。
与此同时,通信带宽是提高控制系统效率和能力的限制条件,如何在节约计算资源的同时有效减轻系统的通信总线负载是航天器控制系统研发过程中的关键问题。基于此,本文将事件触发机制与容错控制方法相结合。当前针对事件触发控制器设计已有较多研究。SAHOO A等[8]对非线性系统控制器和事件触发条件同时进行设计,研究了单输入单输出系统的自适应神经网络事件触发控制律。LI Y X等[9]提出了一种针对单输入单输出非线性系统的模糊自适应事件触发控制律。以上研究主要针对单输出非线性系统设计事件触发控制策略,针对多输入多输出系统的研究还较少,比较典型的系统就是航天器的姿态系统。针对航天器的事件触发控制器设计研究中,SUN S等[10]基于扰动理论进行设计,有效降低了状态信号更新频率,但是其复杂的事件触发机制不利于节约计算资源,也未能考虑航天器受到的外部干扰。LIU Y等[11]针对刚体航天器设计了一种基于事件触发机制的滑模控制器,能够处理系统中的不确定性和外界扰动,但是需要知道未知扰动以及未知参数的上界值。ZHANG C X等[12]针对执行器故障设计了基于学习观测器的事件触发控制器,但未进一步将力矩分配到执行器,并且其基于状态估计量以及故障干扰观测量共设计了两个事件触发机制,其中任一事件触发条件满足时均会引起控制信号的更新,无法得到控制器的最小更新间隔。
总的来说,以上针对航天器的事件触发控制器设计研究中,考虑执行器故障的情况较少。因此,面对航天器功能的日益增多和总线负载能力的限制,以及复杂环境下飞行器姿态控制中故障率增高导致的任务失败问题,本文提出了一种在事件触发机制下航天器执行器故障的自适应容错控制方案,以期解决总线通信压力大、姿态控制执行器卡死和部分失效的问题。
本文的结构如下:首先,介绍了航天器姿态模型,以及事件触发机制相关定义并描述了控制目标;接着,提出了基于事件触发机制的容错控制器,证明了其稳定性以及有效避免了Zeno现象;最后,给出了部分数值仿真结果以及结论。
1 数学模型与问题描述

1.1 数学模型
(1)
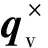
(2)
航天器的姿态动力学方程描述如下[13]
(3)
式中:J=JT∈R3×3为航天器转动惯量矩阵,由固有转动惯量J0和时变转动惯量ΔJ共同组成,即J=J0+ΔJ;u∈Rn为执行器实际输出力矩;D∈R3×n为控制分配矩阵;d为外部扰动。
考虑执行器发生失效故障或者卡死故障,数学表达式为
(4)

σ)E(t)τ(t)+d
(5)
为了简化控制器设计,在航天器执行器出现失效或卡死故障的情况下,对姿态动力学模型作如下假设。


假设3当执行器发生故障时,控制力矩分配矩阵D总能保证D(In-σ)E(t)DT为正定对称矩阵。
注1:若D(In-σ)E(t)DT非正定,则该对称矩阵存在为0的特征值,即姿态系统中至少有一轴是不可控的,为欠驱动系统。而在实际中,为保证系统的可控性,执行器大多冗余配置,因此假设3合理。
1.2 问题描述
航天器的姿态动力学控制问题可以分为两部分进行讨论,第一部分是姿态容错控制问题,第二部分是减轻控制系统负载与能源消耗问题。
针对姿态容错控制问题,本文的控制目标可以由1.1节的推导模型得出,即针对姿态控制系统的执行器发生失效和卡死故障的情况,设计控制律τ(t)实现对姿态的稳定控制,当t→∞时,存在qv→0并且ω→0,或者qv、ω收敛于一个包含零点的任意小的邻域内。
针对减轻控制系统负载与能源消耗问题,需要对航天器姿态控制系统的结构进行分析,如图1所示。从图中可以看出,姿态控制系统由通信网络连接着物理系统和信息处理系统,通信网络在两个系统之间负责传递系统的状态信息和控制指令,形成系统感知-决策-控制的闭环。

图1 航天器姿态控制系统结构
分析图1可知,在以上的一个总线数据传递周期内,存在三个时间延迟t1、t2和t3。其中,t1表示传感器采集信息后通过通信网络总线传递到航天器机载计算机的传输时延;t2表示航天器机载计算机任务调度和信息计算造成的时延;t3表示航天器机载计算机传达的控制指令到达执行器的时延。
而航天器的通信总线除了要负责以上两个系统的信息交互,还要传递数管、热控等多个分系统的指令。为了保证航天器的整体性能,避免总线数据的丢包以及时间延迟,需要尽量减少总线的负载,而减小负载的同时,也降低了系统的能耗。基于减少通信负载的出发点,此处引入事件触发控制思想,通过减小控制器到执行器之间的通信次数来减小系统的通信负载。
2 基于事件触发的姿态自适应容错控制
从XING L T[14]的针对多输入单输出系统的将事件触发机制与控制信号整体大小相关联设计的补偿执行器故障的容错控制器中获得启发,本文中的事件触发机制与控制器参数、系统性能参数以及滑模变量的大小相关联。由于滑模控制需要系统状态首先收敛到滑模面,所以本文事件触发的思想就是将事件触发机制与系统状态到滑模面的距离相结合。当系统状态距离滑模面较远时,此次允许的测量误差也较大,可以有更长的更新间隔;当系统状态距离滑模面较近时,触发机制阈值会变得更小,可以针对系统状态进行更精确的控制以确保其到达滑模面。
2.1 事件触发姿态自适应容错控制器
下文将针对航天器姿态模型,考虑执行器故障,设计基于事件触发机制的容错控制器。
首先,设计一个简单的滑模面为
S=ω+kqv
(6)
式中:k>0为设定的常值参数。此时引理1成立。
引理1[5]:选择合适的控制器使航天器姿态在选取的滑模面(6)上滑动,则当t→∞时有qv→0,q0→1以及ω→0成立。
对滑模面进行求导,并将式(1)和式(5)代入,可以得到
D(In-σ)E(t)τ(t)+d+
(7)
(8)
(9)
基于假设1,可以进一步得到
(10)
综合式(8)到式(10),可以得到
(11)

接着,基于事件触发的思想,设计实际控制信号和事件触发机制分别为
τ(t)=v(ti), ∀t∈[ti,ti+1),i=1,2,3,…
(12)
(13)
式中:v(t)为中间连续控制信号;e(t)=τ(t)-v(t)为测量误差;0<α<1,ξ>0,k1>0为控制参数。由e(t)的定义,可以得到
τ(t)=v(t)+e(t)
(14)
为了方便控制器设计,设定如下变量
(15)
由假设3可得χ>0恒成立,同理可得β>0。虽然β、P中各元素真值未知,但均不随时间发生变化,可以采用自适应方法进行估计。由此可以进一步设计中间连续控制律为
(16)

(17)
式中:λ1>0、λ2>0、γ1>0、γ2>0均为设定的控制器参数。
2.2 证明系统稳定性

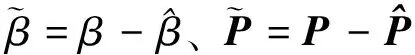
(18)
对Lyapunov函数进行求导,并将式(7)代入,可以得到
(19)
将不等式(11)和事件触发控制器的式(12)、(14)、(15)、(16)代入到式(19)中,可以进一步得到
(20)
将自适应更新律式(17)代入式(20)中,可以进一步得到
(21)

(22)
接下来,引入一个常数η,其满足0<η≤k1(1-α),则式(22)可以进一步转化为
(23)
定义λmax(J)为转动惯量矩阵J的最大特征值,令
(24)
(25)
式中:Δ具体形式如下
(26)
由此可以得出,事件触发姿态控制器可以保证闭环系统的全局一致最终有界稳定,系统中所有的跟踪误差信号都能够最终收敛到边界内,边界的范围为
(27)

2.3 证明有效避免Zeno现象
此处需要证明存在一个时间t*>0,满足∀i∈Z+,{ti+1-ti}≥t*。由e(t)=τ(t)-v(t),则在∀t∈[ti,ti+1)时间间隔内,可以得到
(28)
注2:本文中使用的事件触发控制方法采用了连续的状态反馈策略,其中自适应更新律需要使用连续更新的系统状态,在实际中属于较强的限制。然而此条件在事件触发的领域广泛使用,可以参考LIU T F[15]、XING L T[16]等的文章;即使在未涉及事件触发机制的航天器姿态控制器设计中也同样需要连续的状态反馈,具体参考胡庆雷[17]等的文章;并且航天器传感器如星敏感器和陀螺的采样频率可达32 Hz[18]。因此,设计一个需要连续状态信号的事件触发控制器是可行的。
注3:本文设计的中间连续控制律中含有不连续的符号函数,为了避免抖振现象,实际中通常采用饱和函数来逼近符号函数。
3 仿真试验及结果分析
为了验证本文提出的基于事件触发的自适应容错控制器的有效性,选择文献[7]中的航天器模型参数,基于执行器正常和故障两种工况,对本文提出的基于事件触发的自适应容错控制策略(Event-triggered Adaptive Fault-tolerant Control-ler, ETAFTC)与文献[7]提出的改进型滑模容错控制策略(Modified Sliding-mode Fault-tolerant Controller, MSFTC)进行仿真对比。其中,航天器固有转动惯量为J0=[350,3,4;3,280,10;4,10,190](kg·m2),时变转动惯量为ΔJ=[1+e-0.1t+2μ(t-10)-4μ(t-20)]Λ(kg·m2),式中,Λ=diag(3,2,1),μ(t≥0)=1且μ(t<0)=0;外部扰动d=[A0(3cos(ω0t)+1),A0(1.5sin(ω0t)+3cos(ω0t)),A0(3sin(ω0t)+1)]T,式中A0=1.5×10-5(Nm)为干扰力矩的幅值;ω0=0.0011(rad/s)为轨道角速度。

图2 航天器四飞轮安装示意图
仿真中采用如图2所示的冗余配置的四反作用飞轮执行器组合,每个飞轮的最大输出力矩为0.5(Nm)。四元数的初值为q(0)=[0.17,-0.26,0.79,-0.53]T,角速度的初值为ω(0)=0。相关控制器参数为k=0.15、k1=1、α=0.8、ξ=0.1、λ1=0.02、λ2=0.06、γ1=0.1、γ2=0.1。
下面分正常和故障两种工况来验证本文设计的事件触发自适应姿态容错控制器的有效性。
仿真工况1:各执行器均正常工作。图3~图6分别为工况1下的姿态四元数、角速度、控制力矩以及事件触发间隔的变化曲线。从图3四元数变化曲线以及图4角速度变化曲线可知,本文在自适应滑模控制的基础上引入事件触发机制,可以有效保证系统各状态量收敛,在150 s左右到达稳定状态,并且稳态误差均在10-3数量级。通过与文献[7]中控制策略仿真结果的对比表明,在工况1下引入事件触发机制,对控制器的动态以及稳态性能影响不大。从图5控制力矩变化曲线可知,控制力矩保持在同一个数值一段时间后再更新,体现了本文设计的事件触发控制器的特点,只有当事件触发条件满足时才会更新执行器控制信号。从图5的事件触发间隔变化曲线可知,在工况1下事件触发间隔较长,通过数据统计,在500 s的仿真时长中共触发195次,平均2.56 s触发一次,其频率为0.39 Hz,文献[18]中提到星敏感器等传感器频率高达32 Hz,若假设其等价于执行器更新频率,本文控制器可以减小98.78%的通信负载,充分说明本文的事件触发控制器在正常工况下可有效减小控制器到执行器之间的通信负载。

(a)工况1下的ETAFTC作用下的四元数变化曲线
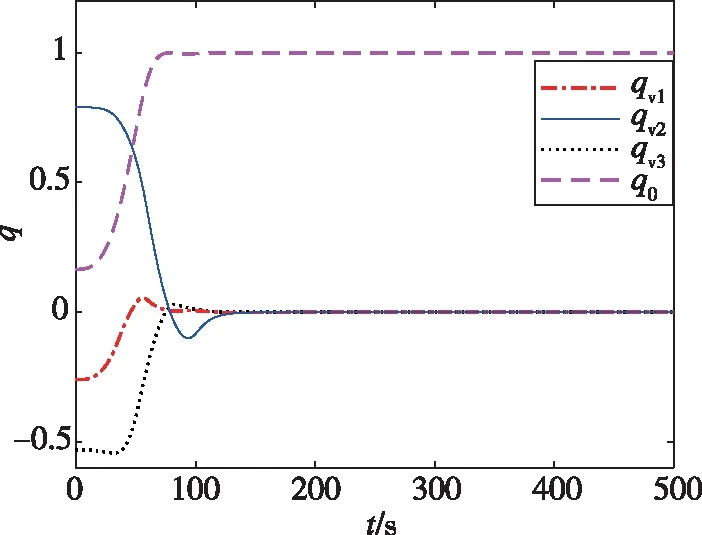
(b)工况1下的MSFTC作用下的四元数变化曲线

(a)工况1下的ETAFTC作用下的角速度变化曲线

(b)工况1下的MSFTC作用下的角速度变化曲线

(a)工况1下的ETAFTC作用下的控制力矩变化曲线

(b)工况1下的MSFTC作用下的控制力矩变化曲线

图6 工况1下的事件触发时间间隔
仿真工况2:滚转轴飞轮50 s时失效80%;俯仰轴飞轮75 s时失效70%;偏航轴飞轮100 s时失效50%;冗余安装的第四个飞轮在150 s时卡死于当时所处力矩。图7~图10为工况2下的仿真结果。从图7和图8中可知,当执行器发生上述故障时,本文设计的事件触发控制器仍然能够使姿态系统在270 s到达稳定,且四元数的稳态误差仍然保持在10-3数量级,角速度的稳态误差为10-4数量级,说明在发生执行器故障情况下本文设计的控制器仍能保持系统的动态和稳态性能。通过与文献[7]中控制策略仿真结果的对比表明,在工况2下引入事件触发机制,对控制性能的影响不大。从图10中可以看出,在发生执行器故障后,事件触发间隔仍较长,在600 s的仿真时长中共触发142次,平均3.08 s触发一次,其频率为0.33 Hz,说明在故障情况下本文的控制器依然可以在保证姿态系统稳定性的同时有效减少控制器与执行器的通信频率,且通信频率并未随着故障的出现而发生频率陡增等情况,进一步说明了该事件触发自适应容错控制器具有良好的鲁棒性。

(a)工况2下的ETAFTC作用下的四元数变化曲线

(b)工况2下的MSFTC作用下的四元数变化曲线

(a)工况2下的ETAFTC作用下的角速度变化曲线

(b)工况2下的MSFTC作用下的角速度变化曲线
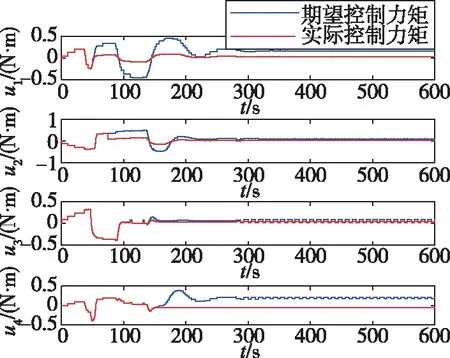
(a)工况2下的ETAFTC作用下的控制力矩变化曲线

(b)工况2下的MSFTC作用下的控制力矩变化曲线

图10 工况2下的事件触发时间间隔
4 结 论
针对航天器姿态模型,综合考虑节约通信资源以及执行器发生部分失效和卡死故障的情况,设计了一种基于事件触发机制的自适应容错控制策略。本文中的控制器不仅能够保证故障情况下的姿态控制精度,而且可以有效降低控制器和执行器之间的通信频率,同时它结构简单、无需故障信息,可以有效节约星载计算机的计算资源。
