初、高中数学知识点差异解析及衔接对策

曹美兰

【摘要】本文针对初中生进入高中后，数学学习出现脱节与断层现象，基于代数与运算、方程与函数、图形与几何和数据整理与概率统计四个方面，分析了初、高中数学的知识点的主要差异.从绝对值、整式、分式、二次根式、一元二次方程及方程组、二次函数的图像与性质和圆七个主要知识点出发，通过典型例题解析，就如何做好初、高中数学教学衔接，提出了具体的教学建议.

【关键词】初中数学;知识点;差异解析

一、问题的提出

随着教育改革的不断深化，初中数学教育已基本完成从“知识本位”向“发展本位”的过渡，初中数学教材中剔除或弱化了大量“繁、难、偏、旧”的内容.新课改基本实现了义务教育阶段想要达到的基础、均衡的目标，同时也极大地推动了素质教育的发展.然而，不少的初中生进入高中后，数学学习却出现了脱节与断层现象，初、高中的数学衔接问题一直备受教师和学生的关注.

目前，许多初中毕业生在中考结束之后都会利用暑期参加一些初、高中数学衔接的培训班，此类培训班的课程大体可分为四种，即：对初中数学知识的再次复习巩固、直接教授高中必修1的数学课程、立足初中知识的奥赛拓展或利用自选的初高衔接教材授课[1].虽然这些培训班或多或少能够对学生起到一定的帮助作用，但授课内容差异较大，质量参差不齐，从长远角度来看，这样的衔接方式并不可取.比如，学生在暑期就已经学习了高一的新课程，到了高一，接触到相同知识点便觉得自己已经掌握，反而会导致学生轻视高中学习.

笔者认为，如果在初中教育阶段适当地穿插渗透初、高中知识点的衔接教学，将有利于初、高中数学的自然衔接.

二、初、高中数学主要知识点差异比较

高考是一场选拔性的考试，同时也是学生迈向高等教育的跳板.在初中教育阶段，教学节奏相对较慢，学生有足够的时间巩固旧知识，内化新知识.同时，通过训练计算能力，理解记忆基本公式，学生即可得到大量的基础分，对学生数学推理能力的要求与高中相比也相对较低.然而，高中课程任务紧、难度大，学生在高一上学期就需要学习完必修1、必修2两本教材，知识点繁多.但无论是在初中数学学习中，还是在高中数学学习中，都可将其知识点大体分成四大部分，即：代数与运算、方程与函数、图形与几何和数学整理与概率统计.（见表1）

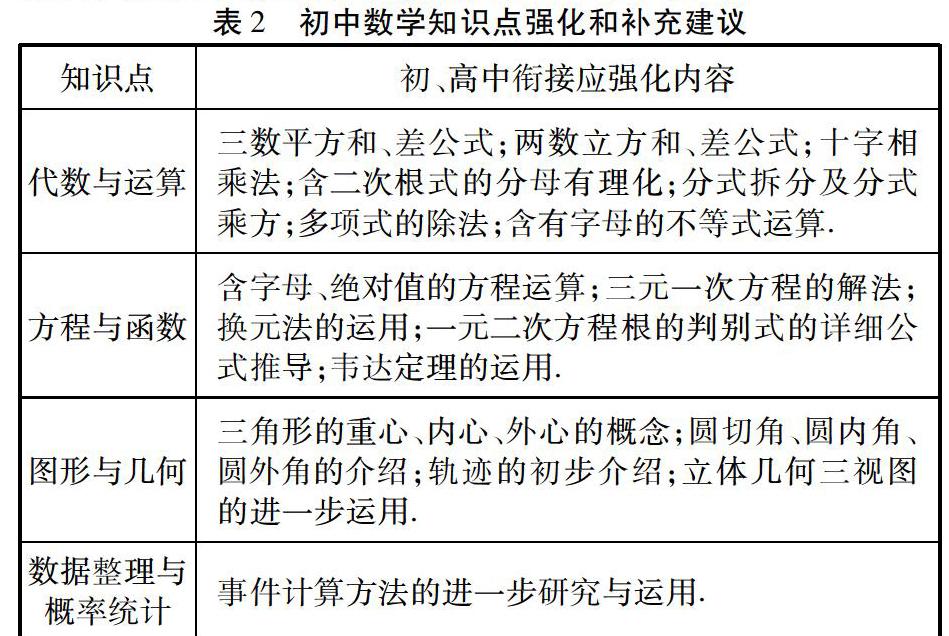
初、高中阶段的知识点是以螺旋式的结构设置安排的，从初中到高中，有的知識点加深了，有的研究范围扩大了，有的更为抽象了[2].要让学生顺利跨过初、高中数学的“高阶梯”，初三数学教师应站在为学生终身发展的角度，在初中教学时进行恰当的铺垫及补充.通过对新、旧初中数学教材及对初、高中数学教材的对比分析，笔者针对不同的数学模块，给出了具体的知识点补充建议.（见表2）

三、初、高中数学主要知识点衔接典型示例解析

作为数学教师，应重视研究新旧知识点的联系与区别，充分利用课堂，有意识地进行知识点的渗透，帮助学生建立知识网络体系.比如，初中教师应注意到高中数学并未专门讲授立方和、立方差公式，所以在教授乘法公式这一内容时，就应有意识地为其补充.研究发现，初、高中知识点的“断层”问题主要出现在七个部分中，即：绝对值、整式、分式、二次根式、一元二次方程及方程组、二次函数的图像与性质和圆.

（一）绝对值

学生在七年级上册的数学教材中就开始接触到绝对值，它贯穿于整个初等数学的始终，并随着知识的发展，不断深化[3].在初中阶段，学生应掌握数轴的概念，理解绝对值的含义，并学会求不含字母的有理数的绝对值.高中则要求学生能够解含有绝对值的不等式.笔者建议在衔接教学时，补充教授含字母的绝对值、简单的含绝对值的方程（不等式）的解法.

（二）整 式

整式的变形是重要的代数式的恒等变形，在初中阶段会要求学生了解整式的概念;会进行简单的整式运算;会利用平方差、完全平方公式进行简单计算;会进行简单的因式分解.整式运算是高中阶段极其常见的运算，但实际上，高中阶段并未再要求学生进行专门学习，许多学生对稍微复杂的乘法公式及十字相乘法等因式分解方法十分陌生.因此，对乘法公式及重要因式分解方法的补充是十分必要的.（见表3）

（三）分 式

分式方程的求解几乎是每年数学中考计算题的必考知识点，但初中对分式的要求也仅停留在恒等式阶段，且方程较为简单.而在高中，则要求学生要掌握求解分式不等式.笔者建议，在初、高中衔接时，应教会学生分式拆分、分式乘方的方法，并教会学生求解可化为一元二次方程的分式方程.

例如，可在初三分式复习的课堂上利用例题，将y=2x+3x+1化为y=m+nx+1的形式（m，n为整数），教会学生分式拆分的基本思想，这样的例题形式简单，学生不仅不会有畏难的情绪，而且又能够体现分式拆分的基本思想，不仅有利于初、高中数学衔接，也能给学生解决初中阶段复杂的分式思考题一些启示.

（四）二次根式

高中数学学习会涉及大量的与二次根式有关的计算，且计算与初中相比较为复杂.根据需要，在初、高中衔接时，学生应掌握最简二次根式、同类根式的概念与运用，学会求解简单的无理方程和不等式，并进一步学习分子（母）有理化.

（五）一元二次方程及二元二次方程组

因高中阶段不再专门学习一元二次方程及方程组的解法，但运用范围仍十分广泛，笔者建议，首先，要巩固学生关于一元二次方程根的判别式的内容;其次，韦达定理在初三数学教材中是选修内容，教师在课时允许的情况下可为学生补充这一知识点;最后，在衔接阶段，教授学生解决二元二次方程组的相关问题.

（六）二次函数的图像与性质

二次函数知识是初、高中数学衔接的重要内容.具体来看，在初中阶段，函数解析式一般是确定给出的，学生有能力利用函数图像求得最值，而到了高中阶段，利用二次函数图像性质求解的题目一般有两种类型：（1）对称轴不固定，区间固定;（2）对称轴固定，动区间.大部分学生难以求解的是第二类问题，在复习完二次函数图像性质之后，教师可给出例题：f（x）=x2+2ax+1（-1≤x≤2）的最大值为4，求a的值.学生容易得出对称轴x=-a，此时教师应引导学生利用函数图像求解此题，首先，函数开口向上，取得最值时对应的x的值只能有两种情况，即x=-1或x=2，引导学生利用分类讨论的数学思想，分情况讨论.若是在初中阶段，因f（x） 的概念尚未引入，教师不一定要要求学生最后能够把答案解出，关键是要拓展学生的思维，引导学生日后求解函数类题目要懂得利用图像性质，要会利用分类讨论思想.

（七）圆

圆的知识点分为两部分，一是与圆有关的角的知识，二是直线与圆、圆与圆的位置关系.许多学生在初中阶段，对与圆有关的概念、定理及弧长计算等问题理解得都较为表面，对定理和计算公式只停留在记忆阶段.笔者建议，在衔接时着重讲授定理和公式的推导过程，训练学生的逻辑思维和抽象概括的能力，此外，可在此时适当地引入轨迹的概念.

四、初、高中数学衔接的教学建议

初、高中的数学衔接，不仅是高中数学教师的任务，也应是初中数学教师要重视的问题;不仅要在初三毕业的暑期做好衔接，也要在初三教学、高一新生入学时做好衔接工作.因此，除了做好知识点方面的衔接，为做好初、高中数学的自然衔接，笔者提出以下建议：

一要强调习惯养成，做好心理疏通.初中生的思维存在着一些表面性和片面性，自我监控能力不强，因此，在衔接阶段可向学生介绍高中学习的基本情況，对新高一学生进行专门的学法指导和心理疏通，教会学生运用一些自我监控的策略.

二要强化思维训练，注重方法衔接.高一新生的思维正处于从直觉形象型向抽象概括型的过渡阶段，虽然初中阶段也十分强调抽象思维能力的运用，但是直观形象的观察还是占据着主导地位[4].一些具体的数学思想方法，学生在初中阶段就已接触，并且在高中阶段运用得更为广泛，例如，配凑法、配方法、待定系数法、整体换元思想、数形结合思想、分类讨论思想及归纳类比思想等.初中数学教师可以在课堂中穿插渗透讲解上述数学思想和数学方法，让学生有直观的感受，能够运用这些方法去解决一些数学问题.

三要加强教师沟通，做好知识铺垫.加强初中数学教师和高中数学教师的沟通，一方面，初中数学教师应对高中数学起始阶段的各方面情况了然于胸，以便为学生日后学习做好铺垫;另一方面，高中教师也应了解初中阶段学生学习的具体内容和知识点掌握程度，以便在高中课堂上能够及时补充缺漏部分，帮助学生快速适应高中数学的学习.

【参考文献】

[1]吴绪坤.利用教材例题与联系做好初高中数学衔接[J].数学学习与研究，2016（13）：90.

[2]郑志培，潘菊玲.新课程背景下初高中数学教学的现状及其衔接对策[J].中学数学，2008（10）：3-6.

[3]邹元磊.关于初高中数学衔接的几点看法[J].基础教育论坛，2016（4）：25-26.

[4]薛锋林.论新课改背景下初高中数学的衔接问题[J].科技创新导报，2011（15）：140.