钢筋钢纤维混凝土T形截面梁受剪裂缝控制试验研究

2020-05-31张晓燕邓翔升宋万万冯蒙李凤兰

华北水利水电大学学报(自然科学版) 2020年2期

张晓燕, 邓翔升, 宋万万, 冯蒙, 李凤兰

(1.华北水利水电大学土木与交通学院,河南郑州 450045; 2.华北水利水电大学河南省生态建材工程国际联合实验室,河南郑州 450045)

受弯构件是钢纤维混凝土的重要结构工程应用对象,其抗弯、抗剪性能与计算方法始终是重要的研究课题。研究结果表明[1-8]:在剪跨区，混凝土在主拉应力作用下斜向开裂以后,钢纤维跨越裂缝起到传递应力的作用,并约束斜裂缝的开展,从而起到了提高斜截面承载力、减小斜裂缝宽度以及改善斜截面破坏形态的作用。同时,钢纤维可以代替部分剪切钢筋承担部分剪力,从而达到优化结构配筋的目的[9]，并可以通过优化钢纤维体积率与箍筋配箍率的组合比例,提高梁的受剪承载力[10]。在最小配箍率条件下,加入体积率为0.75%的钢纤维具有良好的抗剪效果[11]。

目前的研究中主要采用矩形截面梁,对于工程中大量使用的T形截面梁,特别是对于高截面薄腹板的T形截面梁尚缺乏研究。为此,本文进行了T形截面梁的受剪性能试验,考虑钢纤维体积率变化的影响,测试了梁的剪压区混凝土应变、箍筋应变、挠度、斜截面开裂荷载、斜裂缝分布等主要性能。当前，钢纤维混凝土梁的斜截面的裂缝宽度和初裂公式仍未统一,还需不断完善关于斜截面的研究。本文提出了斜截面开裂剪力和斜裂缝宽度的计算公式。

1 试验概况

1.1 原材料

本次试验采用P·O 42.5普通硅酸盐水泥;粗骨料为粒径5～16 mm的碎石;细骨料为天然河砂;粉煤灰掺量为30%;钢纤维采用上海哈瑞克斯铣削型钢纤维,长32 mm,等效直径0.8 mm,长径比为40。钢纤维混凝土设计强度等级为C50;钢纤维体积率ρf=0.8%、1.2%、1.6%;配合比按照绝对体积直接设计方法计算确定[12-13],并通过拌合物性能试验进行适配调整,保证拌合物坍落度在150 mm左右,符合大流动性混凝土的工作性能要求[14-17]。试验梁每组2根,共6根。每组梁伴随6个150 mm150 mm×150 mm立方体试块和3个直径150 mm、高300 mm的圆柱体试块。实测钢纤维混凝土的标准立方体抗压强度fcu、劈裂抗拉强度ft和圆柱体的抗压强度f′c见表1。

表1 钢纤维混凝土强度实测值

1.2 梁的设计与成型

本试验设计制作T形梁的截面高度700 mm、腹板宽度120 mm、翼缘宽度320 mm、高度100 mm。梁长4 m、跨度3.5 m。剪跨比λ=2.5。纵向受拉钢筋为4根φ20 mm的HRB500级钢筋(配筋率1.21%),分两排放置,排距为40 mm。架立筋为4根φ10 mm的HRB400级钢筋。腰筋为2根φ10 mm的HRB400级钢筋。箍筋为φ6 mm间距300 mm的双肢HRB400级钢筋,实测抗拉屈服强度460 MPa、极限强度625 MPa。梁纵向受拉钢筋两端焊接在10 mm厚的钢板上,确保支撑处的锚固。

1.3 加载与测试方法

试验采用液压千斤顶加载进行两点对称集中分级加载,剪跨区长度为1.61 m,如图1所示。

图1 试验梁的尺寸及钢筋布置图(单位:mm)

试验梁上安装4个应变计(C1、C2、C3、C4),布置在靠近加载点翼缘处,用于测量混凝土应变;3个电子位移计(F1、F2、F3),分别布置在试验梁跨中和支座处,测量其跨中的挠度;在剪跨区支座与加载点连线的箍筋上粘贴4个应变片测量箍筋应变。本试验在计算结果的基础上进行分级施加荷载,按计算极限荷载值的10%左右对试验梁进行分级加载,持荷10 min以上,使裂缝充分发展,以便能更好地观察裂缝。

2 试验成果分析

2.1 裂缝分布与破坏形态

各T形截面试验梁的破坏形态如图2所示。在初期加载时,试验梁纯弯段底面首先出现少许弯曲裂缝;随着荷载不断增加,弯曲裂缝向上延伸。

图2 各T形截面试验梁的破坏形态

SF0.8A/B梁的初始斜裂缝出现在剪跨区腹板中间靠近端部处,SF1.2A/B梁的初始斜裂缝出现在剪跨区腹板中间靠近中部,SF1.6A/B梁在剪跨区的初始裂缝分布得更加均匀,如图2所示的红色部分裂缝。斜裂缝沿倾斜方向延伸至支座和荷载点,并随荷载增长逐渐形成一条主要的剪切裂缝。随后斜裂缝数量基本不再增加,主裂缝宽度不断增大。最终在达到极限荷载后,试验梁均发生斜截面剪切破坏。

由图2可见,SF1.6A/B梁的斜裂缝基本遍布了整个剪跨区,裂缝间距较小,说明钢纤维使梁发生了显著的应力重分布。SF1.2A/B和SF0.8A/B梁的裂缝数量较少,主裂缝也较早形成。随着钢纤维体积率的增加,初裂强度Vcr也有明显的提高,梁的初裂倾斜角度随之增大,裂缝开裂宽度减小，这说明钢纤维对试验梁的抗裂影响显著,有效改善了其裂缝分布和破坏形态。试验梁的斜截面开裂测试详细情况见表2。

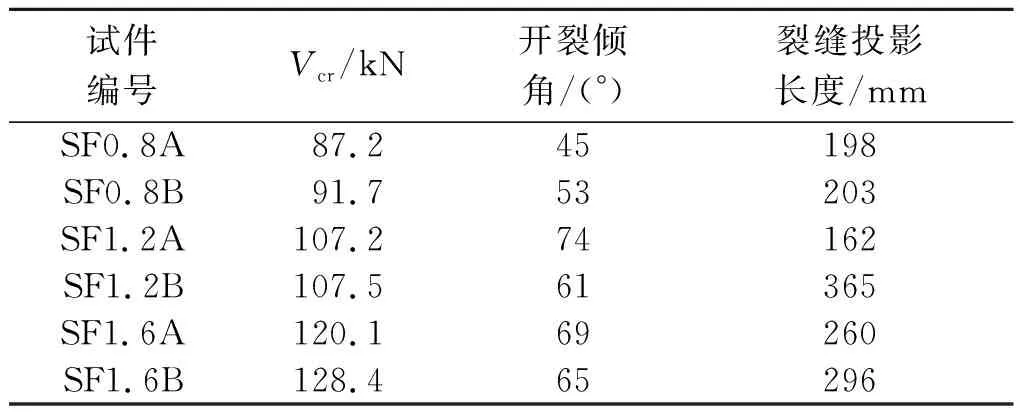
表2 试验梁斜截面开裂测试结果

2.2 剪压区混凝土应变

试验梁剪压区混凝土的荷载-应变关系曲线如图3所示。

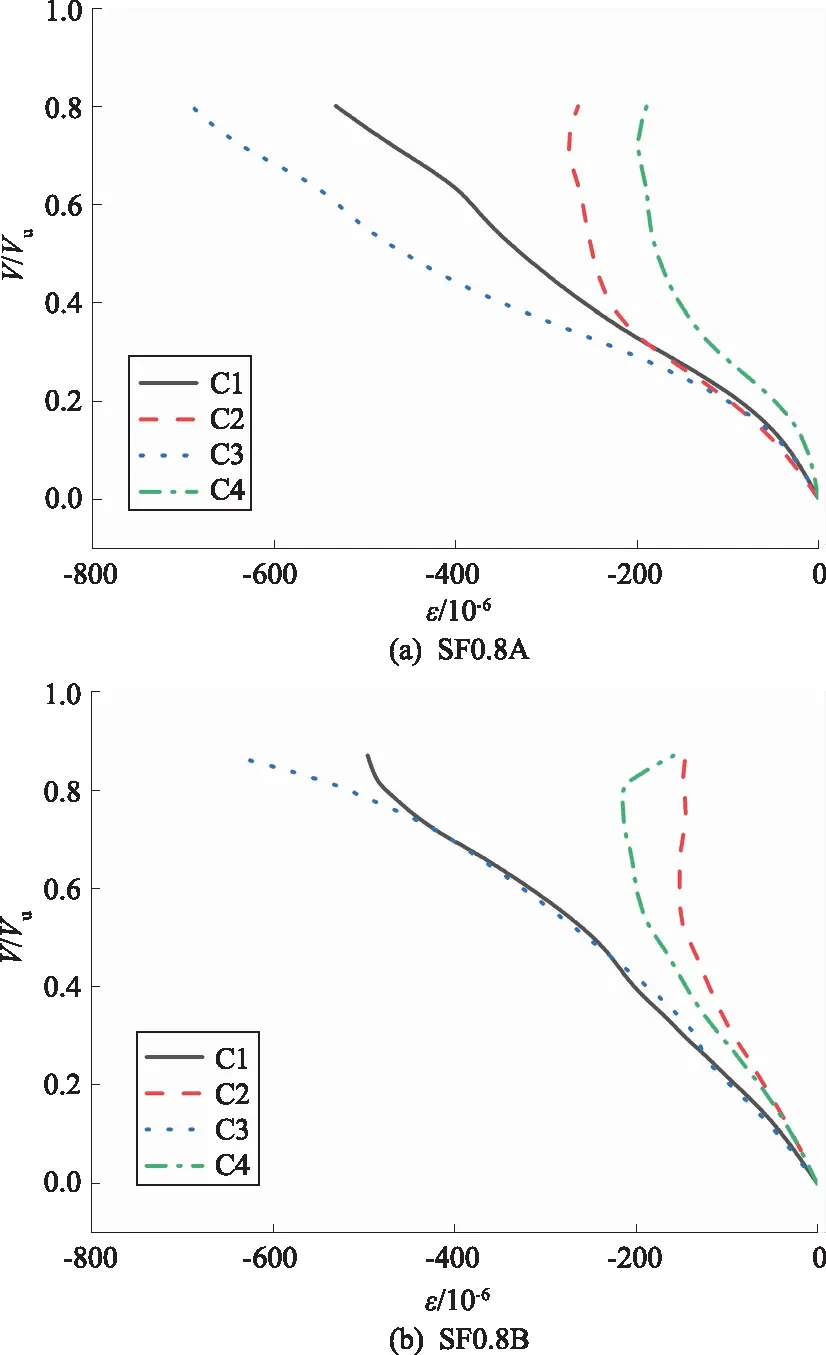
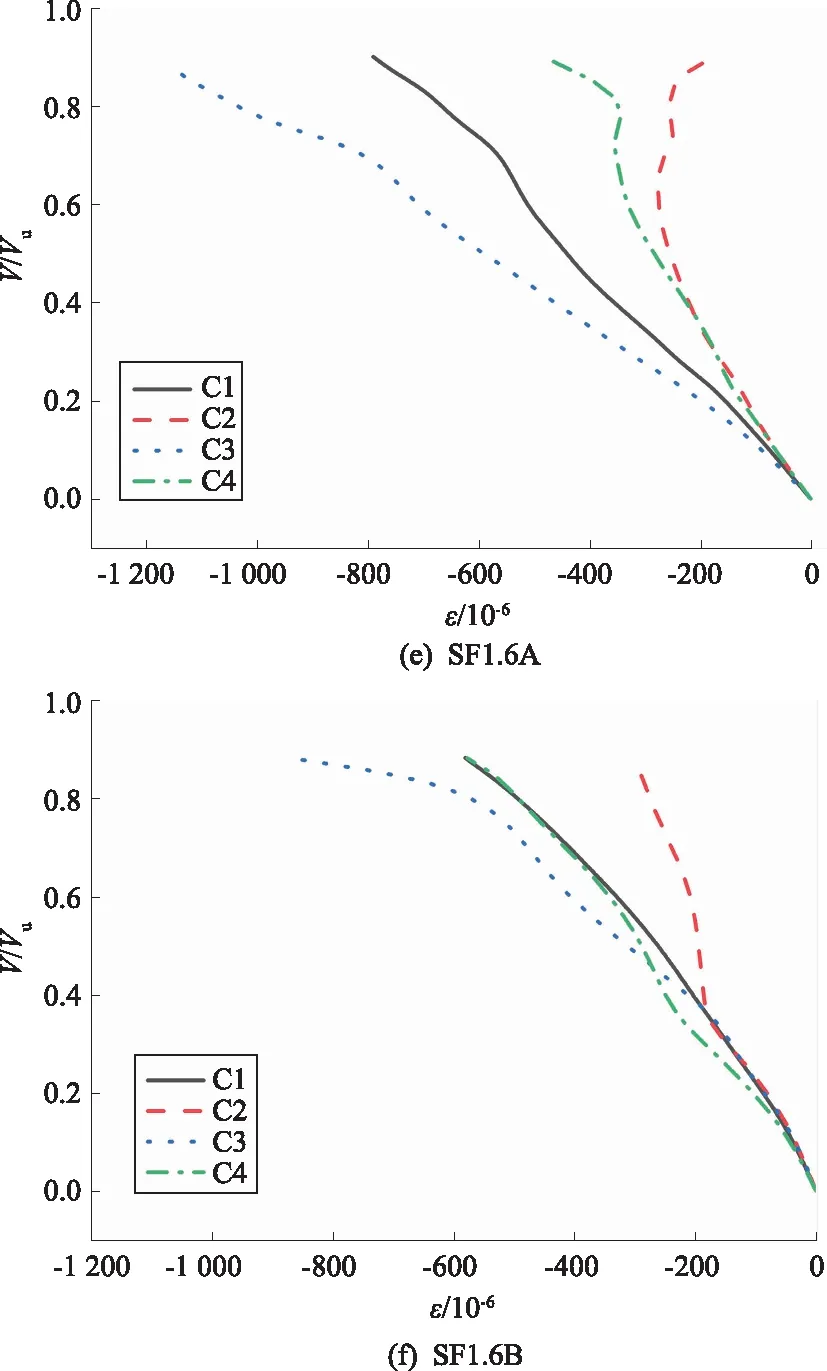
图3 试验梁荷载比值-混凝土应变关系曲线

图3(a)—(f)表明，试验梁剪压区上边缘的应变显著大于下边缘的,说明越靠近上部边缘的混凝土受到的剪应力越大。图3(a)显示，随着荷载增加,裂缝延伸至翼缘,梁的中和轴不断上升,受压区截面面积减小,从而导致翼缘部分受到的压应力急剧增大,混凝土应变增速也随之加大。图3表明，C2和C4应变计到后期出现应变降低的现象,说明中和轴变化较大,到达了翼缘附近。

图3(a)—(f)显示，各梁的受压区混凝土均未出现挤压破坏情况,这说明了试验梁的受压区未达到破坏临界值。随着试验梁钢纤维体积率的增加,受压区混凝土的应变值快速增加,SF1.6A梁的最大应变值比SF0.8A梁的最大应变值多了一倍,这是由于钢纤维提高了混凝土受压区的抗拉强度,相应的混凝土梁受压区也受到更大的剪应力影响,因此应变值增长较大。

2.3 箍筋应变

试验梁的荷载-箍筋应变关系曲线如图4所示。图中箍筋应变值为试验梁左右两侧对应的箍筋应变平均值,本文箍筋的屈服应变为0.002 3。

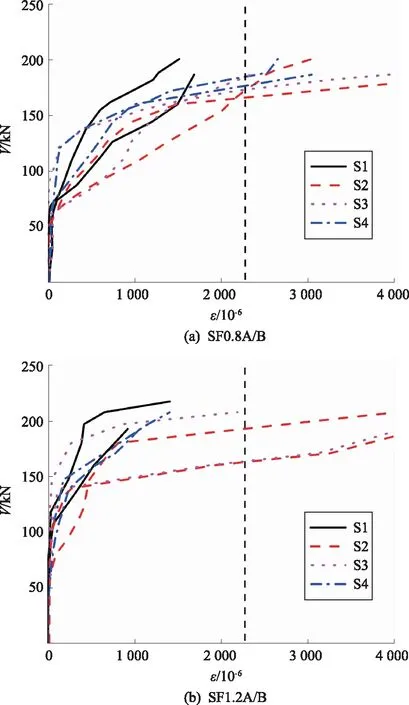
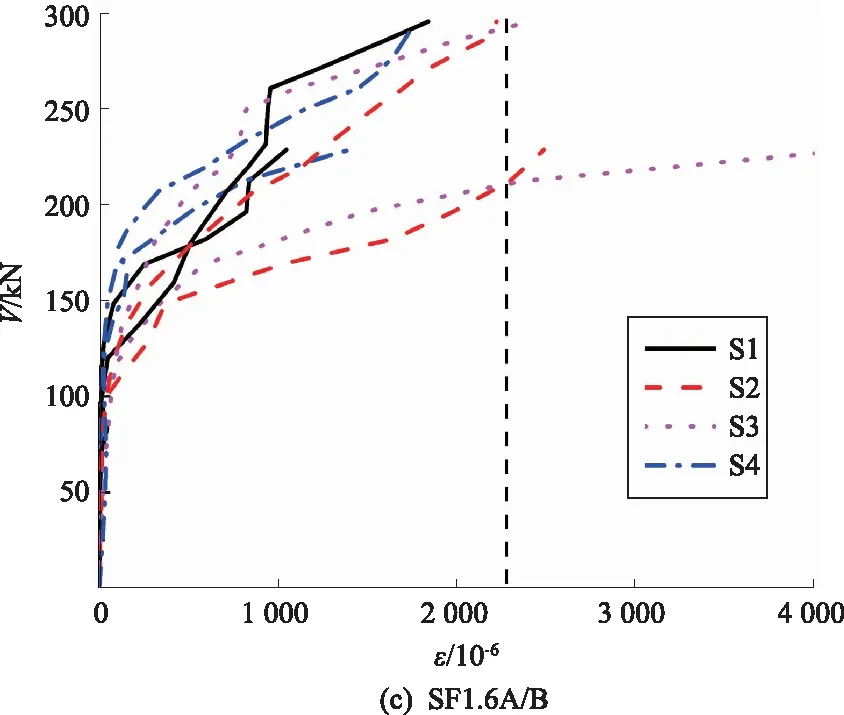
图4 试验梁荷载-箍筋应变关系曲线

在加载至斜裂缝出现前,箍筋承受的剪拉力较小,箍筋应变也较小。斜裂缝出现后,由于钢纤维仍承受一定的拉应力,箍筋应变增长较缓慢。随着斜裂缝的加宽,钢纤维不断被拔出,主要的受力箍筋承受的剪力增大、应变也快速增加,最终在试验梁破坏前屈服。同组两根试验梁的箍筋应变趋势基本一致,SF0.8A/B梁的箍筋应变值突变较早,说明受剪开裂较快;SF1.2A/B和SF1.6A/B梁都是在荷载达到100 kN后应变值才开始出现突变,且应变增长缓慢,说明钢纤维延缓了箍筋的应力集中,最终提高了试验梁的抗剪承载力。

SF0.8A/B梁的箍筋S1的应变较小,箍筋S2、S3、S4均达到屈服;SF1.2A/B和SF1.6A/B梁的箍筋S1和S4的应变较小,箍筋S2和S3均达到屈服,说明钢纤维增强了试验梁的剪力传递能力,钢纤维限制了裂缝向剪压区的延伸,减缓了试验梁剪压区高度的递减,增强了剪压区混凝土的抗压性能,提高了梁的抗剪能力。

2.4 斜裂缝宽度

试验梁的斜裂缝宽度随荷载的变化情况如图5所示,斜裂缝宽度取自裂缝与箍筋相交处。

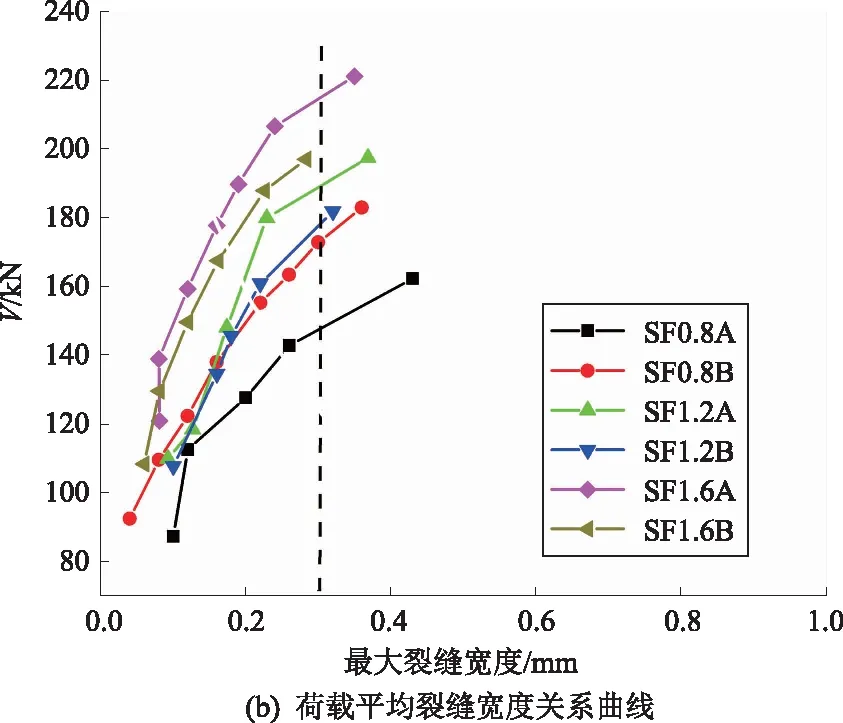
图5 试验梁荷载-裂缝宽度关系曲线

随着钢纤维体积率的增加,最大斜裂缝宽度开展速度减缓,且斜裂缝宽度达到正常使用状态限值(0.3 mm)时的荷载也对应增大。这说明钢纤维能有效延迟T形梁的斜裂缝开展,阻裂效果显著。图5(b)中的平均斜裂缝宽度变化与最大斜裂缝宽度的变化规律基本上保持一致,随着钢纤维体积率增加,试验梁剪跨区的斜裂缝数量增多,平均裂缝宽度增长速度较缓。钢纤维对低配箍率试验梁的抗裂性能影响较大,能显著提高其开裂荷载,说明钢纤维具备能够部分替代箍筋的能力。

2.5 跨中挠度

试验梁荷载-挠度的关系曲线如图6所示,图中的挠度为两端位移与跨中位移的合计。

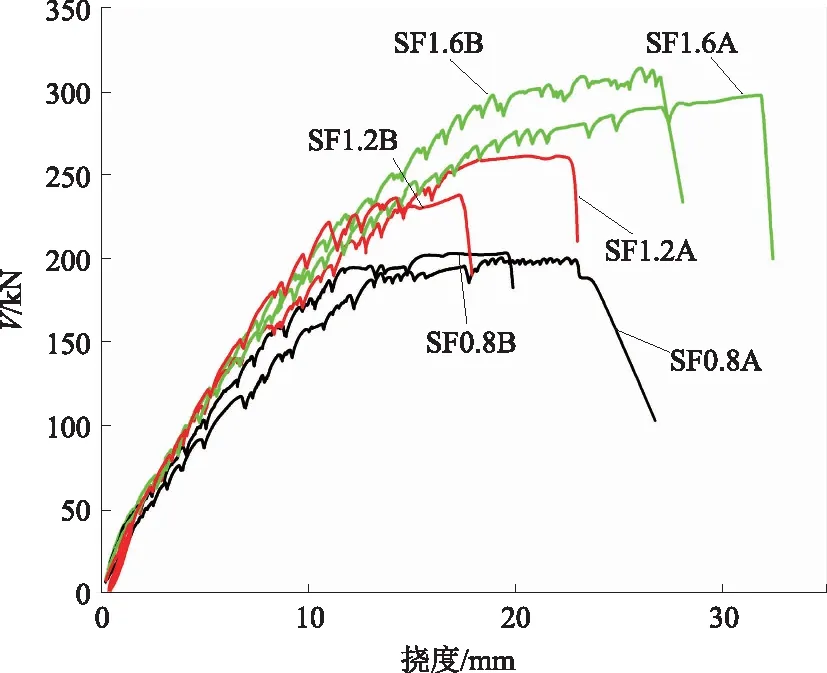
图6 试验梁的荷载-跨中挠度关系曲线

由图6可知,每组两根梁的挠度变化基本上一致,其中A梁加载破坏,B梁加载到破坏前一级停止加载。SF0.8A与SF0.8B梁的挠度发展路径基本一致,前期处于弹性阶段,基本上呈线性增加；加载到200 kN左右,强度缓慢增长,而挠度快速增加,说明试验梁进入塑性阶段。高掺量钢纤维试验梁关系曲线的斜率明显大于低掺量钢纤维梁的,说明钢纤维对斜裂缝开展产生约束作用,限制了裂缝的开展,同时钢纤维增强了混凝土与钢筋间的销栓力作用,提高了试验梁的刚度,从而在同样的荷载下,梁的曲率会更小。SF1.2A梁的极限挠度比SF0.8A梁的增大了1.1%,SF1.6A梁的比SF0.8A梁的增大了43.4%。说明钢纤维的增韧效果非常显著,有效地提高了试验梁的挠度。

3 计算方法

3.1 斜截面开裂剪力

钢纤维混凝土梁受剪开裂前,最大拉应力在试验梁的底部,主要受到纵向受拉钢筋的有效约束,由于混凝土的抗拉性能较弱,因此，在斜截面开裂计算中需要考虑纵筋的影响。试验梁的箍筋对初裂影响甚微,可忽略不计。试验梁的翼缘对初裂影响也较小,为方便计算,也忽略不计。因此,钢纤维混凝土试验梁的斜截面开裂剪力Vcr可按如下公式计算[5]:

(1)

式中:λ为试验梁的剪跨比;ρ为试验梁的纵向钢筋配筋率;fft为钢纤维混凝土的抗拉强度;b为试验梁的腹板宽度;h0为试验梁截面的有效高度。

试验梁斜截面抗裂剪力实测值与计算值的比较如图7所示。实测值与计算值之比值的平均值为0.93,离散系数为0.067。

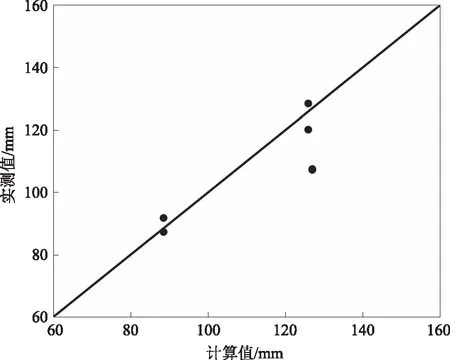
图7 试验梁开裂实测值与计算值对比

3.2 斜裂缝宽度

目前国家规范中还没有关于梁斜裂缝宽度的计算公式,赵顺波等通过大量的试验提出了矩形截面梁斜裂缝宽度的半理论半经验计算公式[6-7]。结合有关矩形截面梁与T形截面梁的研究,翼缘对裂缝影响较小,可忽略不计。因此,可以根据箍筋应变与混凝土应变的关系,对斜裂缝宽度进行预测,基本公式如下:

(2)

(3)

(4)

式中:ωweb为平均裂缝宽度;ωweb,max为最大裂缝宽度;σsv,m为箍筋的平均应变值;Esv为箍筋的弹性模量;Zc为试验梁剪压区的压应力合力点到纵向受拉钢筋合力点的距离;m2为箍筋应力与裂缝宽度间的变化系数;m3为不均匀系数;c为支座到梁裂缝的水平投影距离;a为试验梁的剪跨长度;lw为试验梁斜裂缝的水平投影长度;z为试验梁截面的受力力臂。

利用本文实测的平均裂缝宽度与箍筋应力的实测值关系,可得:

m2=1.55-1.24λf。

(5)

式中λf为钢纤维含量特征值。

根据试验梁的平均斜裂缝宽度与最大斜裂缝宽度的关系,可得:

m3=2.19-0.71λf。

(6)

试验梁钢纤维与混凝土的影响弱化了箍筋应力的初期增长,初裂后的箍筋应力增长基本呈线性增长。因此,考虑这两段箍筋应力变化,得到箍筋应力的计算公式:

(7)

Vs=0.19(V-1.23Vcr)+7.65。

(8)

式中:Vs为试验梁的箍筋应力计算值;Asv为试验梁的配箍率;s为试验梁的箍筋间距;V为试验梁的剪力荷载;Vcr为试验梁的初裂荷载。