考虑相关长度误差的含水层渗透系数反演研究

2021-10-13李株丹刘登川申同庆

节水灌溉 2021年9期

李株丹，刘登川，申同庆，朱磊

（1.宁夏大学土木与水利工程学院，银川750021；2.旱区现代农业水资源高效利用教育部工程研究中心，银川750021）

0 引言

详细准确的描述非均质含水层水文地质参数的空间分布特征，是准确预测地下水流动和污染物运移过程的基础[1]。Yeh提出了一种基于地质统计的参数估计反演方法，称为连续线性估计算法（Successive linear estimator），即SLE 算法[2,3]。该算法能够获取含水层水力参数的空间分布信息，是一种可靠而有效地刻画含水层非均质性的反演方法。在实际工程中，渗透系数作为水文地质数值模拟的主要参数，准确描述其空间分布特征具有非常重要的意义[4]。

许多学者在提高渗透系数反演精度的研究上做了大量的工作，Carrera 和Van 等[5,6]分析了观测数据的质量和数量在反演计算时对反演结果的影响，利用有效的数据去做反演计算时，容易得到比较好的反演结果。王文娟等[7]通过研究不同观测井、抽水井间距、抽水速率大小和采样时间等对反演精度的影响，提出了抽水试验的优化设计方案，反演精度明显提高。Mu 等[8]通过数值实验分析得到了改变观测井数和抽水试验数会对渗透系数反演结果造成的影响，当增加观测井数和抽水试验数时，能够减小渗透系数模拟值与真实值之间的误差。蒋立群等[9]通过改变抽水试验次数分析了渗透系数反演精度的提升程度，随着抽水试验数的增加，反演精度也在逐步提升，当抽水实验数增加到一定程度时，即观测信息过多时，反演精度的提升越来越小。Yu 等[10]研究了在非均质性很强的土壤中收集观测资料时，观测数据的获取较困难。通常，在假定含水层均质各向同性、等厚和无限延伸等条件下，野外现场抽水试验是能够有效地获取观测信息，但是这些假定与实际情况往往不符。现场抽水试验也受试验区条件、经费等各种因素限制，有限的观测数据很难准确地描述含水层空间分布。因此，渗透系数实测值很难准确而有效地获得，目前也尚缺乏渗透系数实测值与反演结果误差的关系。本文将基于情景模拟，通过连续线性估计算法研究在相关长度误差影响下的含水层渗透系数的反演精度，并结合数值实验得到渗透系数实测值数据量与反演结果误差的关系。因此，该研究对实际工程中选取较适宜的渗透系数实测值数据量具有现实和指导意义。

1 模型描述

1.1 连续线性估计方法(SLE)

SLE 算法是将水力参数(即渗透系数)与水头在估计过程中的非线性关系结合起来，通过使用线性估值来处理，最大化提高数据的有用性，将均值和协方差矩阵输入模型初始值作为先验信息，以满足控制方程的求解条件[11,12]。SLE 算法中的迭代过程可以概化为贝叶斯迭代，同时更新均值和协方差矩阵。在稳定流条件下，用水头值估计渗透系数可以用以下公式迭代式求解：

式中：上标r表示迭代次数；(xm)表示在xm点第r次迭代的模拟值；hj*(xj)表示在xj点处水头观测值；hj(r)(xj)表示在xj点处水头模拟值；ωmj(r)为权重项，表示第r次迭代时，在xj点处观测到的条件水头与模拟水头之差[即hj*(xj)和hj(r)(xj)]对点xm处估计值的贡献。

1.2 反演结果的评价准则

在本文中使用一阶矩L1，相关系数Cor，决定系数R2，均方根误差RMSE来评价SLE 反演结果优劣的标准[13]。L1，RMSE，Cor的数学表达式为：

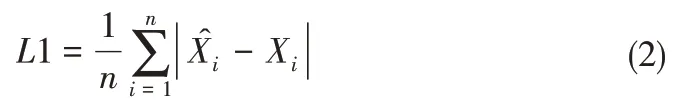
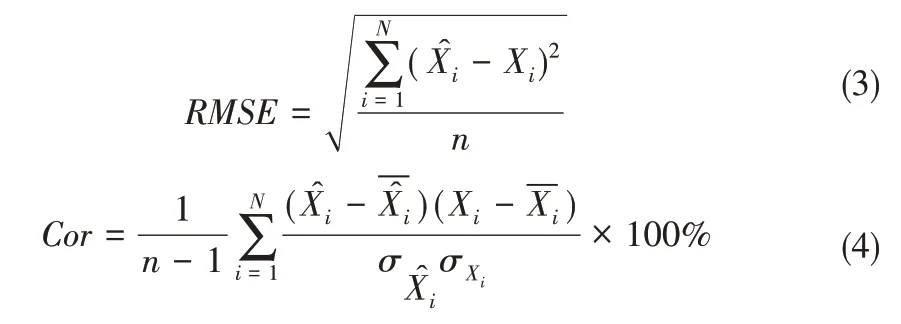
式中：n表示数据的个数；和Xi分别表示第i个观测井的水头观测值和估计值；和分别指观测值和估计值的均值；和σXi分别表示观测值与估计值的标准差。

其中，一阶矩L1 指绝对误差；均方根误差RMSE值大于0，指估计值和观测值偏差的平方与n比值的平方根；相关系数Cor取值在−1 到1 内，表示观测值与估计值之间的相关程度；决定系数R2在0到1之间取值，是相关系数的平方。当L1和RMSE数值越小，Cor和R2数值越大时，则观测值与模拟值之间的误差越小，此时模拟结果越好。

2 数值实验

本研究将采用基于SLE 算法的VSAFT2 软件进行一个综合的数值算例，该软件能够进行2D 地下水水分运动、溶质运移的正演及含水层地质参数的反演计算，计算结果可用Tecplot软件处理和显示。

2.1 正演计算

设定水力参考随机场为一个（10 000×10 000）m2的水平二维饱和非均质稳定流含水层，包含10 000 个（X、Y轴分别为100 个）单元，设定渗透系数的均值为6.5 m/d，方差为4，相关长度X、Y轴均为3 000 m，具有指数协方差函数。含水层的左右边界均设定为隔水边界，上、下边界设定为定水头边界，水头值分别取5 m、4 m。模型共设置一组抽水试验，每次抽水试验共设置9口井，其中包括1口抽水井P1，既抽水又观测，8口观测井，抽水流量为3 000 m3/d。含水层渗透系数K的参考场见图1，正演计算水头值见图2。

图1 K的参考场Fig.1 The material field of K

图2 水头等值线图Fig.2 Head contour map

2.2 SLE参数反演

反演计算设定参数除相关长度外均与正演计算时设定数值相同，计算时改变反演相关长度，通过依次增加K实测值数据量计算得到渗透系数估计值的空间分布。相关长度、K实测值数具体取值可见表1。

表1 相关长度、K实测值数取值Tab.1 Value of correlation scale and K field measured volume

3 结果与讨论

3.1 渗透系数反演结果

当渗透系数K反演的相关长度取值和正演相关长度相同，均取值为3000m，且K实测值数据量没有增加时，渗透系数K反演结果如图3所示。

当减小渗透系数K反演的相关长度，以1 500 m 为例，K实测值数据量分别设置为0、16、32、48、64、80个时，渗透系数K反演结果如图4所示。

图3中反演相关长度为3 000 m，图4反演相关长度为1 500 m，且K实测值均为0 个时，比较可知，当反演相关长度为1 500 m 时，参数K的模拟值越偏离真实值，误差较大。因此表明，当减小反演相关长度数值时，会对参数K的反演结果有影响，反演结果误差会随着相关长度数值的减小而增大。

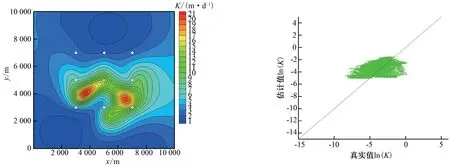
图3 相关长度取值3 000 m时K反演结果(R2=0.171)Fig.3 K inversion result at correlation scale of 3 000 m(R2=0.171)

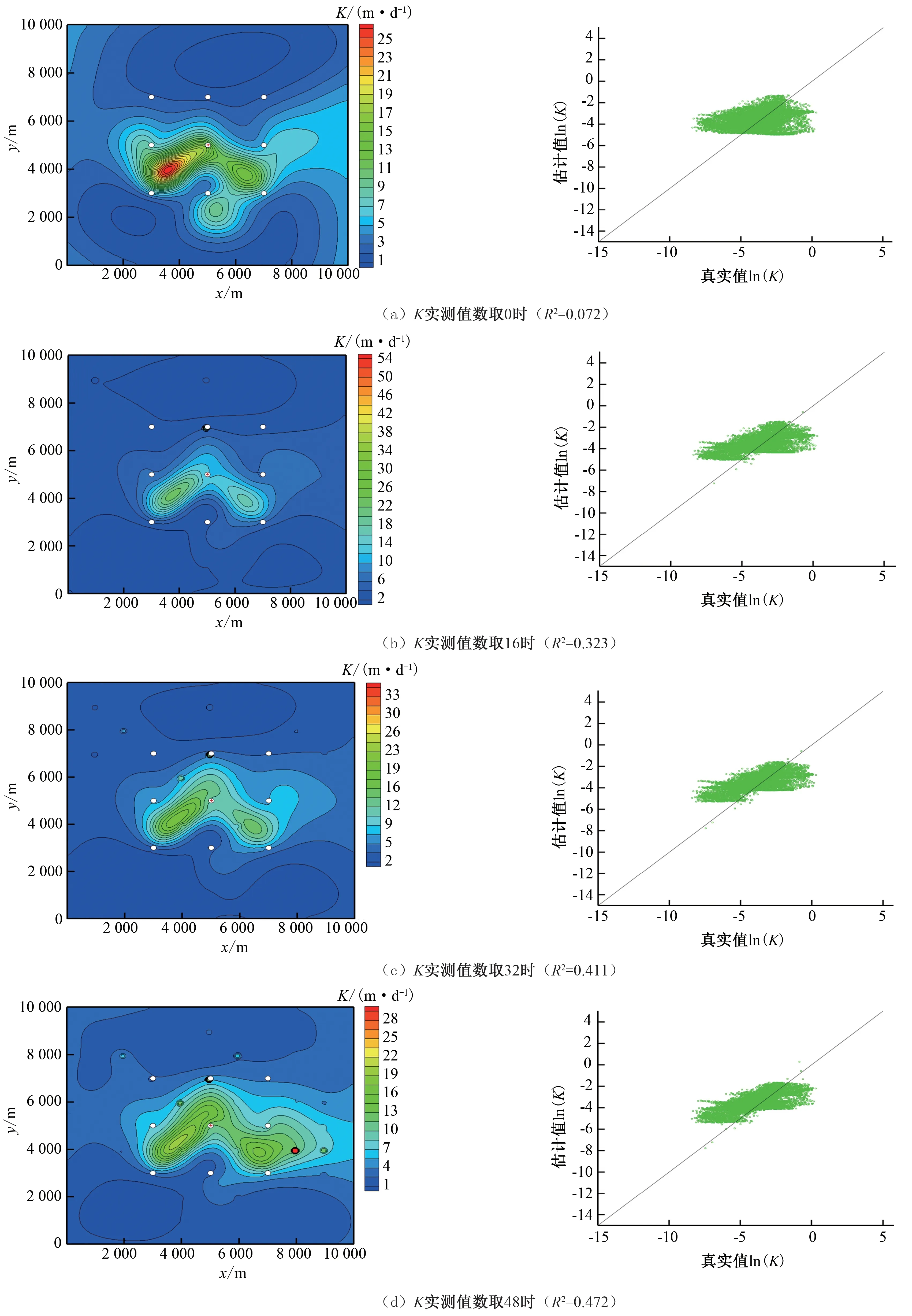
图4 相关长度取值1 500 m时K反演结果Fig.4 K inversion result at correlation scale of 1 500 m

分析图4散点图可知：当K实测值数为0 个时，散点图中的大部分估计值较分散，偏离45°线较多；当K实测值数为16个时，左右两侧的估计值开始向45°线靠近；当K实测值数为32 个时，边缘散开的估计值开始趋近于45°线；随着K实测值数依次增加为48、64、80 个时，由散点图可知，大部分点越来越趋近于45°线，说明估计值越来越接近于真实值，当K实测值数为80 个时，散点图围绕45°线均匀分布，反演结果最好。由此可知：随着横坐标K实测值数据量的增加，含水层渗透系数的估计值越来越接近于真实值，即估计值与真实值之间的误差越来越小，渗透系数反演结果越好，反演精度越来越高。

3.2 误差分析

随着反演相关长度数值在正演相关长度基础上依次减小时，参数K的反演结果误差与K实测值数据量之间变化的关系如图5所示。由此分析：随着反演相关长度依次减小10%、20%、30%、40%直到100%时，以竖直黑实线为基准，当横坐标K实测值数在30 个以内时，纵坐标L1、RMSE值越来越小，Cor、R2值越来越大；当横坐标K实测值数大于30 个时，纵坐标L1、RMSE值依然在减小，只是减小的幅度越来越平缓，同理Cor、R2值增加的程度也越来越小。由表2可知，当K实测值数据量由0、16、32、48、64、依次增加至80 个，反演相关长度减小10%时，决定系数R2的值分别为0.161、0.382、0.463、0.522、0.564、0.580，参数K反演精度分别提高了136%、180%、223%、251%、260%；当反演相关长度减小50%时，决定系数R2的值分别为0.071、0.321、0.413、0.472、0.522、0.561，参数K反演精度分别提高了355%、480%、570%、642%、700%；当反演相关长度减小90%时，决定系数R2的值分别为0.052、0.062、0.113、0.174、0.203、0.262，参数K反演精度分别提高了21%、142%、241%、302%、420%。

随着反演相关长度数值在正演相关长度基础上依次的增加时，参数K的反演结果误差与K实测值数据量之间变化的关系如图6所示。由此分析：随着反演相关长度依次增加10%、20%、30%、40%直到100%时，以竖直黑实线为基准，当横坐标K实测值数在30 个以内时，纵坐标L1、RMSE值越来越小，Cor、R2值越趋近于1；当横坐标K实测值数大于30 个时，纵坐标L1、RMSE、Cor、R2均变化幅度较小，越来越平缓。由表2可知，当K实测值数据量由0、16、32、48、64、依次增加至80 个，反演相关长度增加10%时，决定系数R2的值分别为0.192、0.383、0.474、0.522、0.565、0.583，参数K反演精度分别提高了101%、145%、173%、193%、203%。当反演相关长度增加100%时，决定系数R2的值分别为0.311、0.392、0.461、0.542、0.523、0.541，参数K反演精度分别提高了25%、48%、74%、67%、77%。当反演相关长度增加200%时，决定系数R2的值分别为0.353、0.384、0.494、0.513、0.495、0.523，参数K反演精度分别提高了9%、40%、46%、40%、49%。

表2 决定系数R2增加值Tab.2 Determination coefficient R2 increment

3.3 讨论

分析图5和图6可知，无论增加还是减小反演相关长度，当K实测值数据仅有16 个，即K实测值数据量较少，相关长度误差存在的情况下，反演结果误差都是比较大的。当横坐标K实测值数据量开始依次增加时，纵坐标R2、Cor的值开始向1 靠近；L1、RMSE值越来越小。分析可知，以竖直黑实线为基准，随着横坐标K实测值数据量的增加，当K实测值数据大于30 个时，各个相关长度误差下的反演结果误差值变化幅度都比较小，虽然呈递增趋势，但是增加的程度越来越平缓。由此可知，横坐标K实测值数据量的增加能够有效地提高含水层渗透系数的反演精度，但是持续的增加K实测值数，直到一定程度时，纵坐标反演结果误差的变化异常缓慢，并没有很大的改变反演精度。比如，减小反演相关长度下，以取值2 700 m 为例，相关长度误差减小10%，当横坐标K实测值从0增加到32 个时，参数K的反演精度提高了185%；由此对比，当横坐标K实测值从32 增加到80 个时，参数K的反演精度只提高了26%，并没有前期精度提高的那么明显。同理，增大反演相关长度，以取值6 000 m 为例，相关长度误差增加100%，前期反演精度提高了48%，后期反演精度只提高了17%。因此，通过数值实验表明，在相关长度误差存在的基础上，K实测值的数据量会对反演结果有影响，K实测值的数据量越多，反演结果越好。但是过多的K实测值数据量会造成数据过剩，当K实测值数达到一定程度之后，观测信息的冗余性使得反演精度提升的越来越慢。因此，对于本文设置的数值实验而言，K实测值数据量应设置在30个以内。

图5 减小反演相关长度下K实测值数据量与反演结果误差的关系Fig.5 The relationship between the measured value of K and the error of the inversion result with reducing the inversion correlation scale

图6 增加反演相关长度下K实测值数据量与反演结果误差的关系Fig.6 The relationship between the measured value of K and the error of the inversion result with increasing the inversion correlation scale