基于近似贝叶斯计算方法的排队模型参数估计

张 岚， 钱夕元

（华东理工大学，理学院，上海 200237）

排队论在社会各个领域都应用广泛，包括银行排队叫号、机场排队取行李、电话排队服务、交通运输等。但在实际应用中，在衡量一个排队模型优劣时，常需基于已知的到达率和服务率计算排队模型的几个重要指标：系统平均队长、排队等候平均队长、平均逗留时间、平均排队时间，而通常排队数据无法直接观测到这两个参数。在估计到达率和服务率，且是否使得排队系统稳定时，贝叶斯推断和估计在排队论中有很大的优势。

贝叶斯早在1763 年就提出贝叶斯公式，并给出贝叶斯估计的思想，根据每一类的样本估计每一类的类条件概率密度，把参数θ看成未知的随机变量，通过对样本观察再求贝叶斯估计。在贝叶斯估计时，首先需要选择先验分布，再确定似然函数，确定参数的后验分布，选择损失函数，最后估计参数。贝叶斯推断在排队系统中的优势：a. 系统稳定性的不确定性可以容易被量化；b. 在参数空间中的限制容易被处理；c. 预期的参数可以直接得出；d. 贝叶斯决策技巧可以直接用于计算排队论中的最优决策。对于M/M/1，除了上述Bagchi 等，Armero 等[1-2]和Choudhury 等[3]研究了这个排队系统下常用衡量效果测度的分布，如系统和排队的顾客数、等待时间以及忙碌期、空闲期的时间长度；并结合泊松间隔到达时间和指数分布服务时间进行贝叶斯推断，并给出联合后验分布。对于非马尔科夫系统：关于G/M/1，G/M/c系统研究较少，其中Wiper[4]分析了Er/M/1 和Er/M/c，研究了间隔到达时间服从爱尔兰分布的排队系统，他用蒙特卡洛模拟方法估计队列长度和等待时间的分布，且阐述了采用独立先验时许多队列的测度不存在。而对于非马尔科夫服务时间，Insua 等[5-6]对M/Er/1 系统强度估计的基础上进一步用蒙特卡洛方法给出了M/G/1 的贝叶斯推断和估计，并使得队列达到均衡状态。Ausín 等[7]通过Coxian 分布模型给出GI/G/1 系统的贝叶斯推断，同时指出他们的方法可以用于估计瞬时队伍大小以及等待时间的分布。

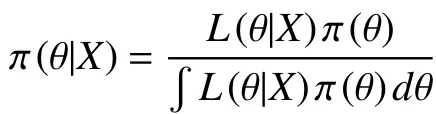
本文运用近似贝叶斯的方法，结合排队论QDC算法的思想对四个经典排队模型进行仿真模拟，给出参数估计与估计效果；并结合实际例子（银行的面对面排队换汇数据）估计参数。

1 模 型

一个排队系统中需要研究每个顾客i的到达时间 ai（或者到达时间间隔δi=ai−ai−1,a0=0）与服务台对他们的服务时间 si。排队系统主要有6 个特征：a. 到达时间的分布 fδ；b. 服务时间间隔的分布fs；c. 服务台的个数K， K∈N；d. 系统的承载能力C，C∈N；e. 顾客数量n，n∈N；f. 服务规则 R。

对于到达间隔时间和服务时间的分布：常用M 表示指数或泊松且独立分布；GI 表示广义独立分布；G 表示广义无独立性假设的分布。C 表示同一时刻系统承载的最多顾客数量。在系统中的顾客只有两种状态：等待或者正在被服务。顾客数量n 包含系统中、即将到达或者已经离开的顾客。服务规则R 表示在队列中顾客如何分配到对应的服务台，最普遍的规则是先到先服务（first come first serve，FCFS）。

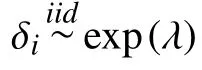
对于单服务台的排队系统，由于顾客和服务台只能处于两种状态，顾客等待服务台或者服务台等待顾客，因此第i 个顾客的离开时间定义为：di=max(ai,di−1)+si。

1.1 对于马尔科夫系统M/M/1的贝叶斯推断

在M/M/1排队系统中，假定到达率和服务率λ 和 µ是未知的。 ta表示 na个顾客到达的总时间，ts表示 ns个顾客服务完成的时间，在排队系统中一般na=ns。由于n个IID 指数分布的和服从Erlang分布，因此似然函数为

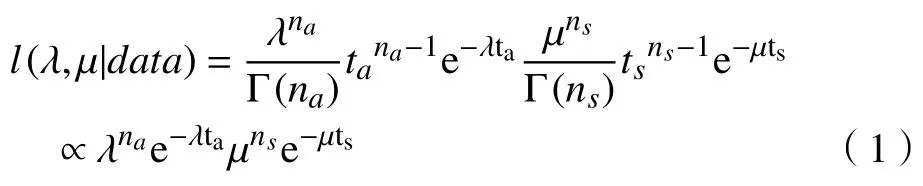
基于似然函数， λ 和µ的共轭先验分布为Gamma 分布。

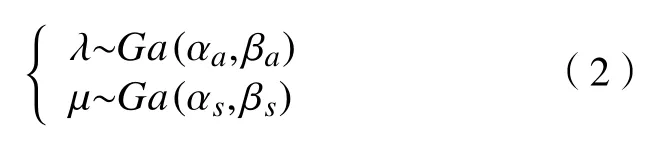
其中αa,βa,αs,βs＞0，后验分布易得

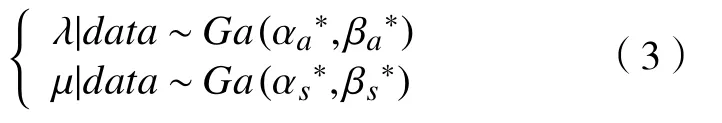
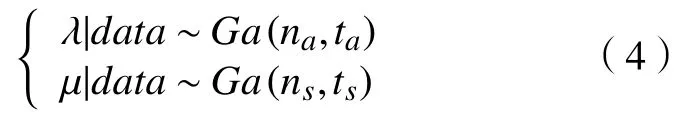
1.2 对于非马尔科夫系统的贝叶斯推断

1.2.1 G/M/1模型

以Er/M/1为例，即到达间隔时间服从Erlang分布。在这个排队系统中，假定到达时间是v 个以λ/ν为参数的指数同分布，则到达间隔时间X|ν,λ ～Er(ν,λ)，服务时间服从以µ为参数的指数分布，先验同M/M/1中Gamma 分布。(ν,λ)的共轭先验分布为

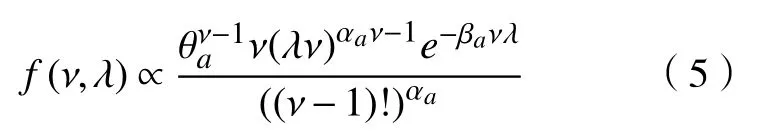
式中：λ ＞0；ν=1,2,···。根据该先验分布可以得到基于ν的 λ的条件分布、 ν的边际分布分别为

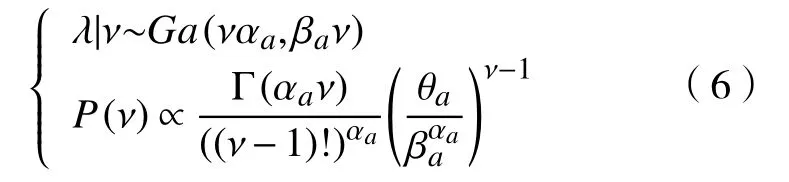
默认地设定θa=1,αa=βa=0，则先验变为f(λ,ν)∝1/λ。基于共轭先验分布，联合后验分布为

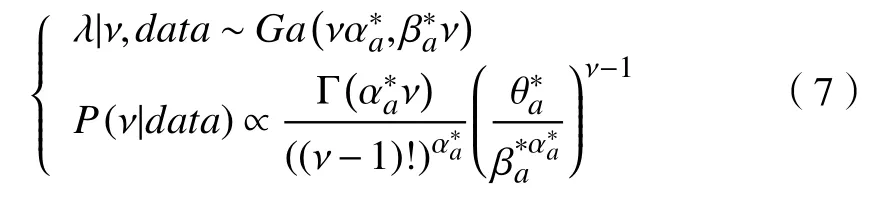
1.2.2 M/G/1模型

以M/Er/1排队系统为例，Insua 等[5]已经提出对该模型的贝叶斯推断过程。假定每个顾客到达的间隔时间是以 λ为参数的指数分布，服务时间服从Erlang 分布。指数分布的共轭先验为Gamma 分布，其后验分布也为Gamma 分布；服务时间服从爱尔兰分布的先验不再赘述，且两者相互独立。

1.2.3 GI/GI/1模型

以GI/GI/1模型为例，假定到达间隔时间与服务时间都服从Coxian 分布或者混合广义爱尔兰（mixed generalized Erlang，MGE）分布，且两者独立。若X 服从Coxian 分布，则以L ，P=(P1,P2,···,PL)、λ=(λ1,λ2,···,λL)为参数，满足

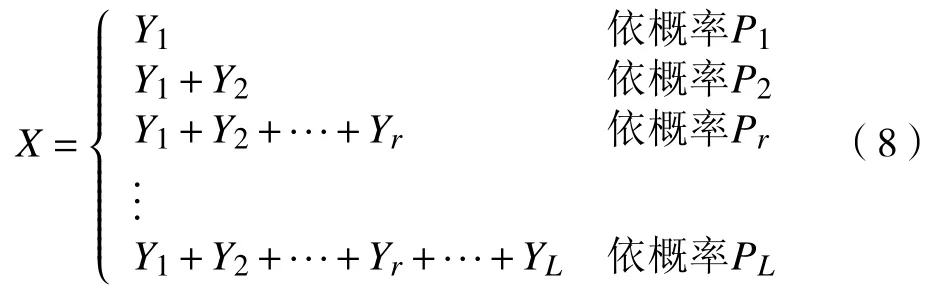
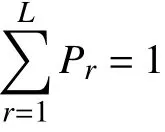
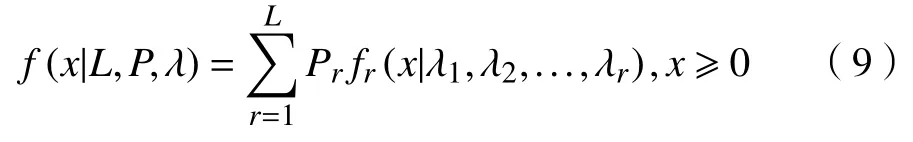
其中fr(x|λ1,...,λr)是MGE 分布的密度函数。若∃i ≠j,s.t. λi≠λj，则

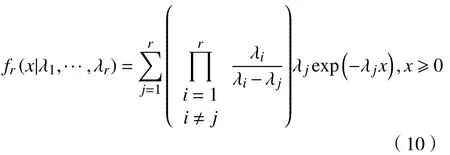
假定L 是已知的，本文基于Ausín 等[7]对Coxian 分布中各参数的无信息先验分布的结论作修改

特别地，令φr=1,∀r=1,···,L。

1.3 基于近似贝叶斯计算的排队系统

在贝叶斯推断中M/G/1，G/M/1，GI/GI/1 模型的似然函数复杂，因此采用近似贝叶斯计算的方法，将重点从似然函数转为人工数据的模拟，则需要选取恰当的先验与概要统计量。在衡量排队系统好坏时，平均等待时间被指出为重要指标，因此将平均等待时间作为第一个概要统计量，其中顾客等待时间可以直接从数据获得，或定义为到达时间减去上一位顾客离开时间。并选取各排队模型下离开时间的各分位数作为第二个概要统计量，能充分反映到达率和服务率在各排队模型中的信息。

基于近似贝叶斯与QDC 思想，给出单服务台的排队系统的参数估计步骤如下：

a. 给出顾客排队数据，并且假定顾客的到达时间a（ 或到达间隔时间）与接受服务的时间s分别服从参数 λ 和µ，离开时间为 d，并给出阈值 ε0以及先验分布π(λ)和 π(µ)。

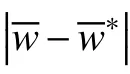
2 仿真与实际数据实验

R 软件中的queue computer 包可以简单地将排队过程呈现出来，并且可得到队列的多个重要统计量，如平均等待时间、平均队列长度等。因此结合queue computer 与近似贝叶斯方法对4 个排队模型进行参数估计。

2.1 M/M/1排队系统

由于先验分布服从Gamma 分布，因此给出选择分布中超参数的3 种方法[12]：

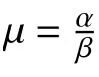
b. 采用分位数，比如中位数和三分位数。检验最终结果是否合理，并与其他不同的选择情况进行比较；

c. 合理地实验，通过经验判断或者尝试后选取合适的 α 与 β。

这里选取第一种方法选取超参数，在该排队系统中，对顾客数n=10 000，λ=1， µ=1/0.9的系统进行模拟。在进行30 次迭代后得到如表1 中的结果，后验分布如图1。

表1 λ 和µ的估计值与标准差Tab.1 Estimation and standard deviation of λ and µ

从表1 可以得到 λ 和 µ的估计值与真实值接近，且后验分布也表明估计效果较好。

2.2 M/G/1排队系统

在这个排队系统中，对顾客数n=60，λ=1，Er(3,1.2)的系统进行模拟。经过实证比较，在选择超参数时，选取中位数和三分位数较合理；在进行30 次迭代后得到如表2 中的结果，后验分布如图2。从表2 的结果可以观察到虽然估计值都靠近真实值，结合后验分布及标准差发现µ的估计效果比 λ好。

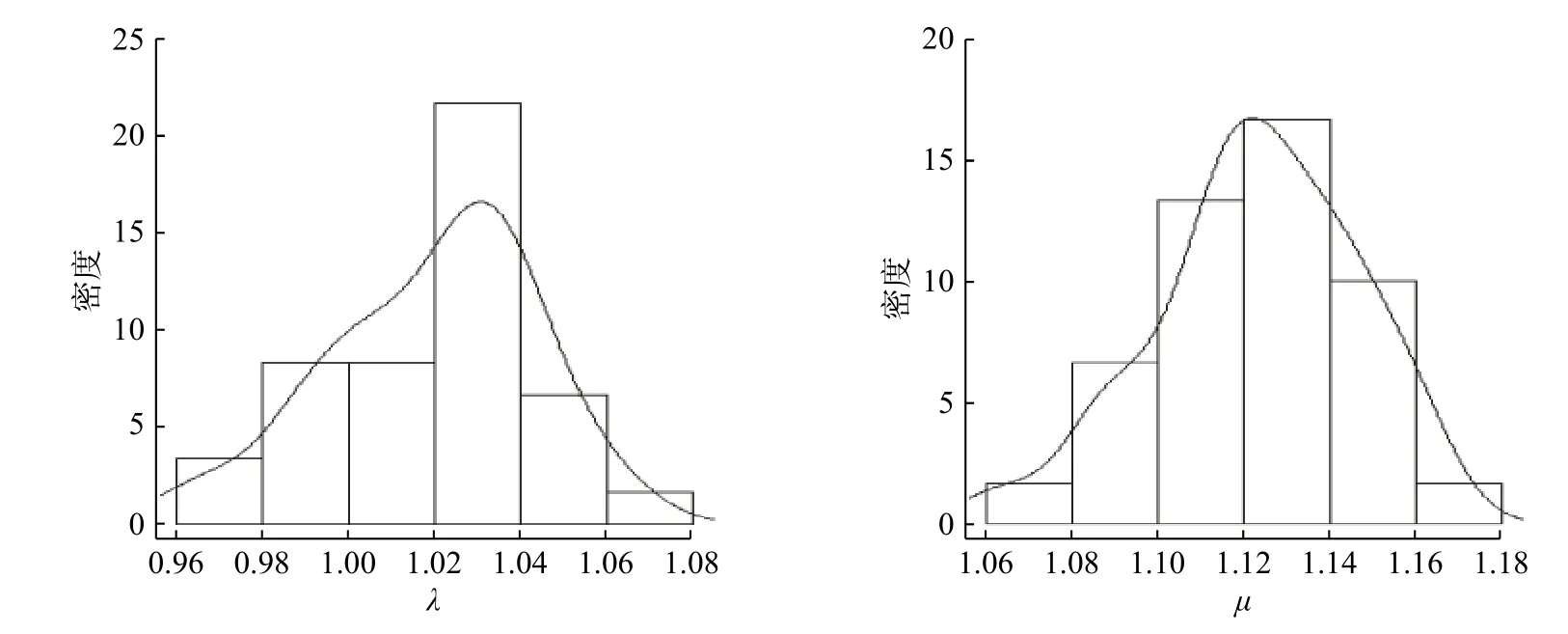
图1 λ 和µ的后验分布图Fig.1 Posterior distribution of λ and µ

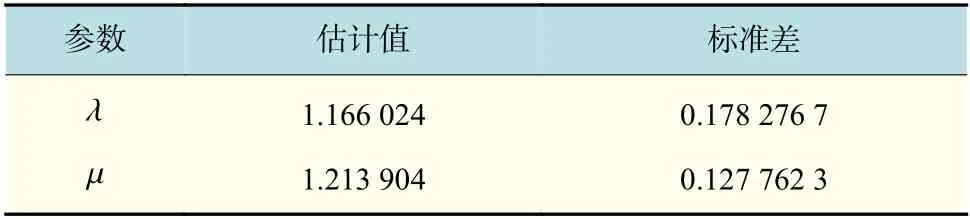
表2 λ 和µ的估计值与标准差Tab.2 Estimation and standard deviation of λ and µ

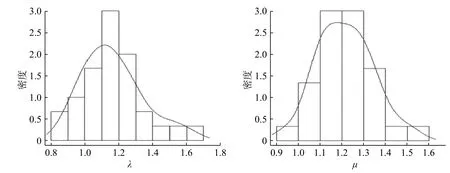
图2 λ 和µ的后验分布图Fig.2 Posterior distribution of λ and µ

2.3 G/M/1排队系统

在这个排队系统中，对顾客数n=100 ，Er(5,0.5)，µ=1的系统进行模拟。经过实证比较，在选择超参数时，选取中位数和三分位数较合理；在进行30 次迭代后得到如表3 中的结果，后验分布如图3。从表3 的结果观察到 λ和µ的估计值接近真实值，从后验分布与标准差的结果比较发现对 λ的估计更准确。

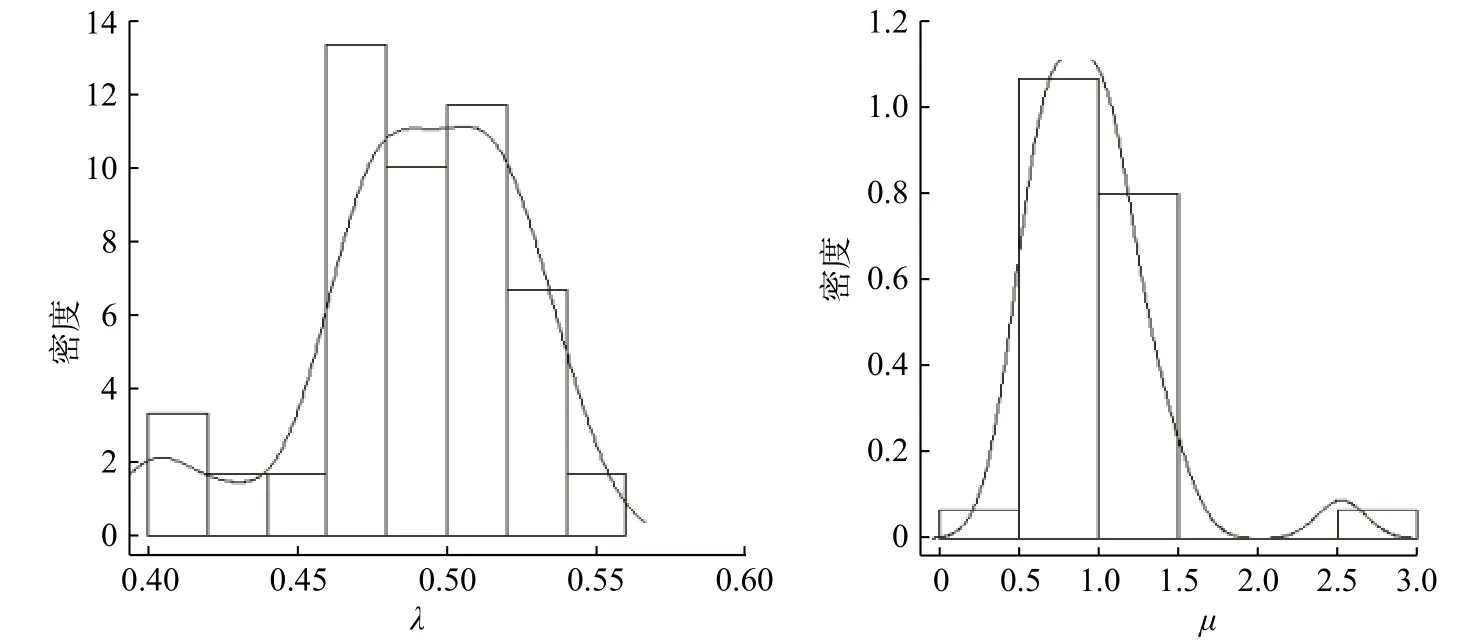
图3 λ 和µ的后验分布图Fig.3 Posterior distribution of λ and µ

表3 λ 和µ的估计值与标准差Tab.3 Estimation and standard deviation of λ and µ

2.4 GI/GI/1排队系统

在这个排队系统中，对顾客数n=300 ，L=4，P=(0.09,0.7,0.01,0.2)，λ=(1.1,1,0.251,0.25)的系统进行模拟。基于修改的先验，在进行50 次迭代后得到如表4 中的结果，后验分布如图4。从表4中可以得到各分量的估计值与真实值相近，但 λ3和λ4估计值有偏离；结合后验分布发现 λ2， λ3， λ4的估计效果相对较差，出现这种情况的原因可能在于Coxian 分布中参数的约束受到概率P 的影响。

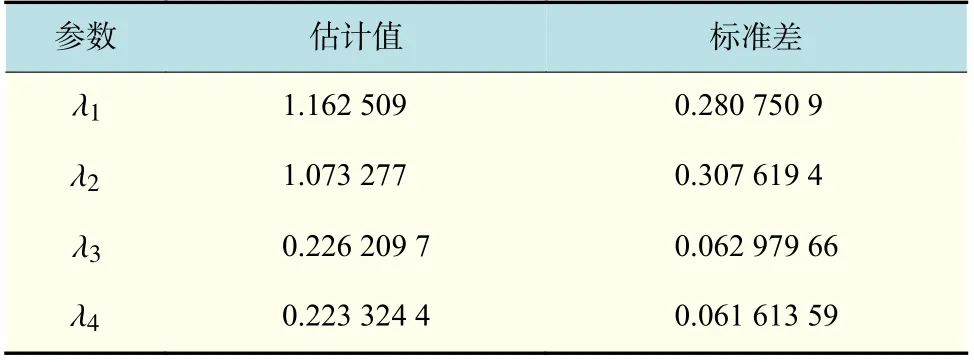
表4 λ各分量的估计值与标准差Tab.4 Estimation and standard deviation of each component of λ

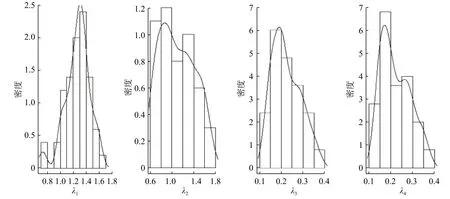
图4 λ各个分量的后验分布图Fig.4 Posterior distribution of each component of λ

2.5 实际数据应用：银行面对面排队外汇交换数据

从http：//iew3.technion.ac.il/serveng 中可以直接得到银行的面对面排队外汇交换的数据，数据记录了14 d 内270 位顾客的排队信息。这类服务需要一个服务台在一周内3 d 从8：30 工作到12：00；两天从8：30 到12：30，16：00 到18：00。为了满足QDC算法中连续性的要求，本文将所有信息根据到达时间升序排序，并做标准化处理。该数据中，平均到达间隔时间为11.99 min；平均服务时间为7.16 min。根据Ausín 等[7]对于L 的研究，在这里设定La=2 ，Ls=1，因此需要对3 个参数 λ进行估计，在50 次迭代后得到如表5 中的结果，后验分布如图5。从表5 中的标准差及后验分布得出，λ1与 λ3的估计效果相对比 λ2好。

表5 λ1,λ2,λ3的估计值与标准差Tab.5 Estimation and standard deviation of λ1,λ2,λ3

为了进一步验证参数估计值的正确性，将Ausín 等[7]研究得到的估计值λ1=0.1， λ2=0.1，λ3=0.14 与本文得到的值分别代入得的拟合数据、实际数据进行比较（如图6），比较发现本文估计参数拟合的数据与Ausin 的拟合数据分布接近，但两者对于 λ1，λ2与实际数据都有差距，因此可能需要进一步提高参数的精确度。

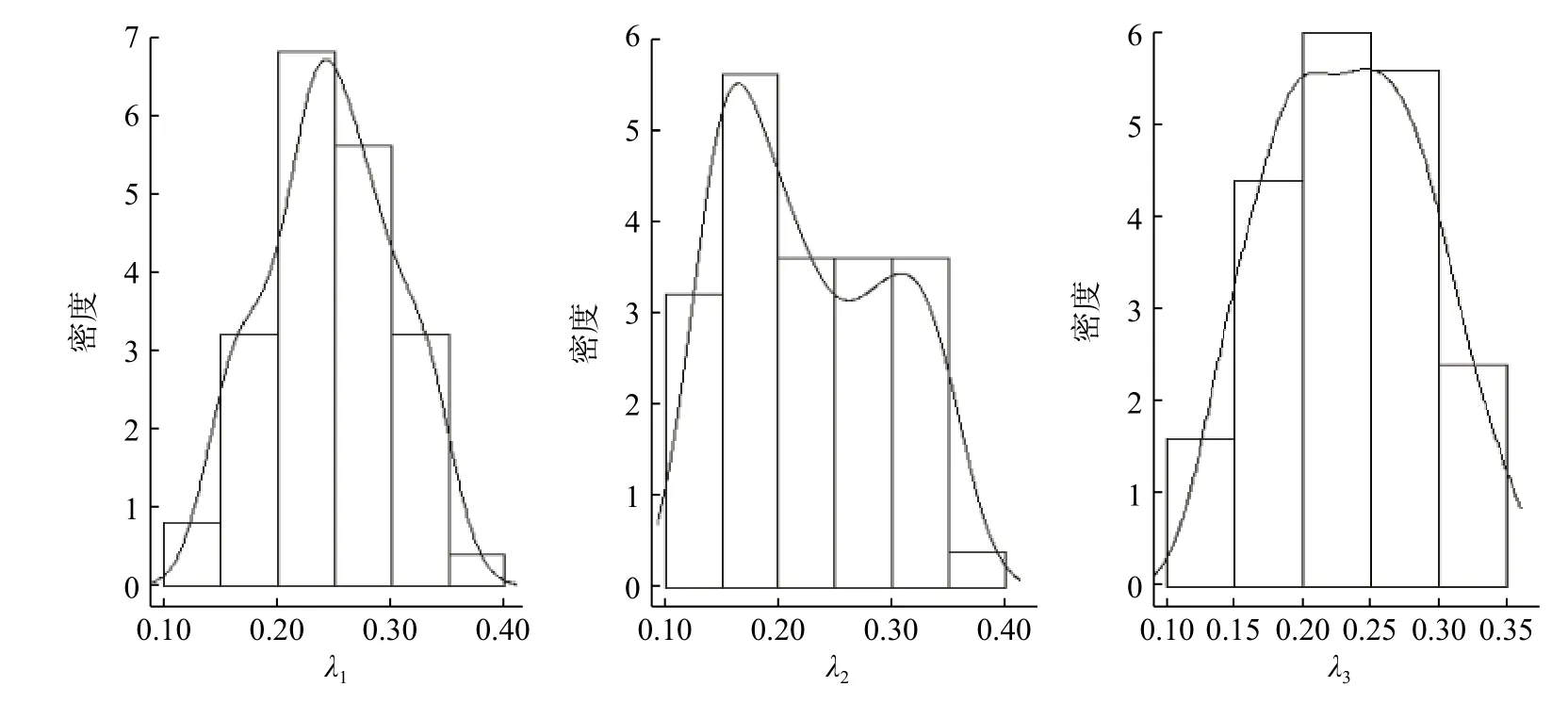
图5 λ1,λ2,λ3的后验分布图Fig.5 Posterior distribution of each component of λ1,λ2,λ3

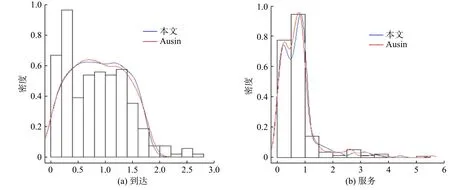
图6 两组拟合数据的分布曲线图Fig.6 Distribution of two fitted data

3 结 论

本文将近似贝叶斯与排队论模型结合在一起，并在4 个排队模型M/M/1， M/G/1，G/M/1，GI/GI/1下给出对应的参数估计值以及估计效果。模拟研究表明，近似贝叶斯方法较排队论传统方法在参数估计上有优势，并且量化了不确定性，解决了复杂排队模型中似然函数难以解析表达的困难。在实际应用数据中也获得了较好的参数估计，但为了提高在复杂模型中参数的精确度需要进一步改进贝叶斯参数估计方法。