基于第一性原理研究三氧化二钇本征点缺陷的热动力学性质
2020-05-30王炳佳刘廷禹姚君涛
王炳佳, 刘廷禹, 姚君涛
(上海理工大学 理学院,上海 200093)
氧化钇(Y2O3)作为一种常见的稀土氧化物,由于其熔点高、透光性好、耐腐蚀等特点,常被用作高温红外材料及激光基质材料[1-2],其禁带宽度大,为6 eV,当掺杂不同稀土离子时可改变材料的物理性能,例如,将5%的Eu3+掺杂在氧化钇材料中,能获得具有高强度荧光的发光材料,被广泛应用在固态激光器件和照明行业[3-5]。由于氧化钇的介电常数大,在半导体器件中也被用作栅极氧化材料[6]。制备氧化钇晶体及粉末时需要在持续高温的环境下完成,这将容易产生大量点缺陷,而带电荷的点缺陷会与掺杂离子交换能量,从而降低材料的发光效率,影响光学和介电性质[7-10]。文献[11]指出, 当研究ODS( oxide dispersion strengthened)铁素体钢时,空位型缺陷可能是影响氧化钇抗辐射性的关键因素。因此,深入研究氧化钇晶体本征点缺陷的基本性质十分必要。
文献[12-13]研究了氧化钇的电子结构及光学性质。Zheng 等[14]利用第一性原理计算了氧化钇中的点缺陷形成能,缺陷形成能作为温度和氧偏压的函数,Zheng 等只考虑了富氧和缺氧两种极端条件下的缺陷形成能,而未给出一般环境条件下的缺陷的基本情况,且未考虑振动熵的贡献。本文通过第一性原理计算,研究氧化钇晶体中的本征点缺陷随温度、氧分压和费米能级的变化规律,以揭示当外部环境发生变化时,点缺陷的类型及稳定性的基本变化规律。
1 研究方法
1.1 电子结构计算
计算选取氧和钇的价带电子分别为4s24p65s64d1和2s22p4。本文应用密度泛函理论(DFT)的VASP 软件计算时,采用了投影缀加波(PAW)方法描述原子实与价电子的相互作用[16-17]。交互关联泛函应用广义梯度近似(GGA)下的PW91 公式[18]。K 点取样采用7×7×7 的Monkhorst-Pack 网格。经过收敛性测试,在精度达到10 meV 的标准时,氧化钇(Y2O3)平面波的截断能为520 eV。

图1 氧化钇晶体结构(灰色原子代表24d 和8b 位置上的钇原子,红色原子代表48e 位置上的氧原子)Fig.1 Crystal structure of Y2O3 (Gray atoms represent yttrium atoms at 24d and 8b, and red atoms represent oxygen atoms at 48e)
1.2 势参数选取及振动熵计算
计算时选择恰当的相互作用赝势可准确地描述出粒子间的相互作用,氧化钇的相互作用势中库仑相互作用是主要部分,库仑相互作用中的长程势

式中:Zi,Zj分别为原子i,j 的有效电荷;e 为电荷量;rij为原子i,j 之间的距离。
本文电子壳模型的短程作用选用Buckingham 势描述,短程势


表1 GULP 软件中两体势的参数Tab.1 Two-body potentials parameters in the GULP software
晶体中的缺陷浓度在热力学平衡状态下保持平衡,亥姆霍兹自由能

式中:U 为内能;Svib为振动熵;T 为温度。
内能和振动熵对自由能的贡献是相反的,当温度极低时,振动熵的值很小,可忽略不计。温度升高,振动熵逐渐成为主要影响因素。在高温情况下,尤其要考虑振动熵对缺陷形成能量的影响。本文使用GULP 程序来计算晶格振动熵,计算时可采用式(4)[19]。

式中:Zvib为振动熵的配分函数;h 为普朗克常数; υ为频率;ωk为角频率;N 为阿伏伽德罗常数;k 为玻尔兹曼常数。
1.3 缺陷形成能的计算
氧化钇的缺陷形成能ΔGf(α, q, P, T)是α 原子的缺陷、价态q、氧偏压P 和温度T 的函数。在考虑振动熵贡献后,缺陷形成能量

式中:Etot(α, q)是带电量为q 的α 原子的缺陷的总能;Etot,p为完整晶体的总能;nα是相比较于完整晶体原子或者离子的增减数量,当nα>0 时,代表α 的空位型缺陷,当nα<0 时,代表α 的填隙型缺陷;εf为费米能级;μα(T, P)为α 原子的化学势;EVBM为完整晶体价带顶能量;Ef为电子相对于价带顶的费米能级;ΔV 为完整超晶胞和含有缺陷的超晶胞之间的平均静电势差值[22];ΔSvib(T)为含缺陷的振动熵与完整晶体振动熵的差,是温度的函数。
当温度和氧偏压变化时,氧的化学势

2 结果和讨论
2.1 晶格结构参数
计算得到氧化钇中氧原子的位置坐标(x, y, z)和晶格常数a,如表2 所示。对比实验值可知,本文的计算结果比文献[24]应用LDA 赝势模拟的数据更接近实验值,且相对误差小于1%。由此可知,本文计算电子结构时所选参数可为下文的点缺陷研究提供合理的计算基础。
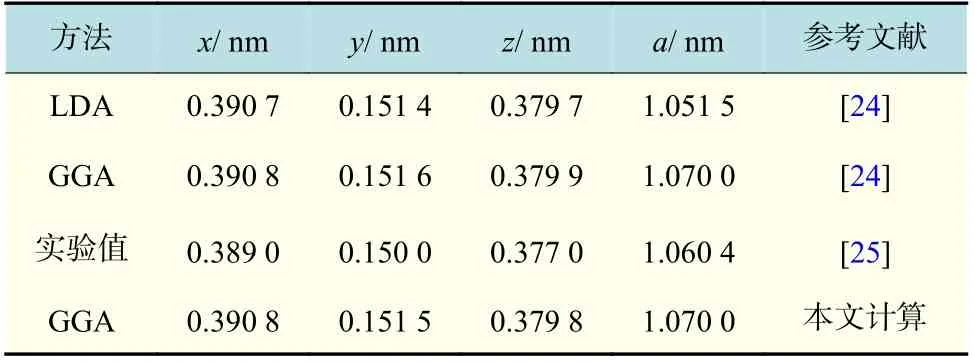
表2 第一性原理计算氧化钇晶体结构数据与实验值对比Tab.2 Calculated and experimental results of Y2O3 crystal structure based on the first-principle
2.2 振动熵计算结果
利用GULP 软件得到了空位、填隙和反位缺陷的振动熵随温度的变化规律,结果如图2 所示。在常温条件下(T<300 K),点缺陷振动熵(TΔSvib)的绝对值变化在0.015~0.39 eV 之间,其对缺陷形成能的影响有限。温度增高会导致振动熵的攀升,在1 200 K 时,Yi的振动熵增加到2.06 eV,而振动熵降低最明显的阳离子空位VY振动熵减少了0.67 eV。与300 K 温度下VY振动熵减少0.043 eV 相比,可知其变化趋势明显。由此可知,高温时振动熵对这类缺陷的贡献是不容忽视的。
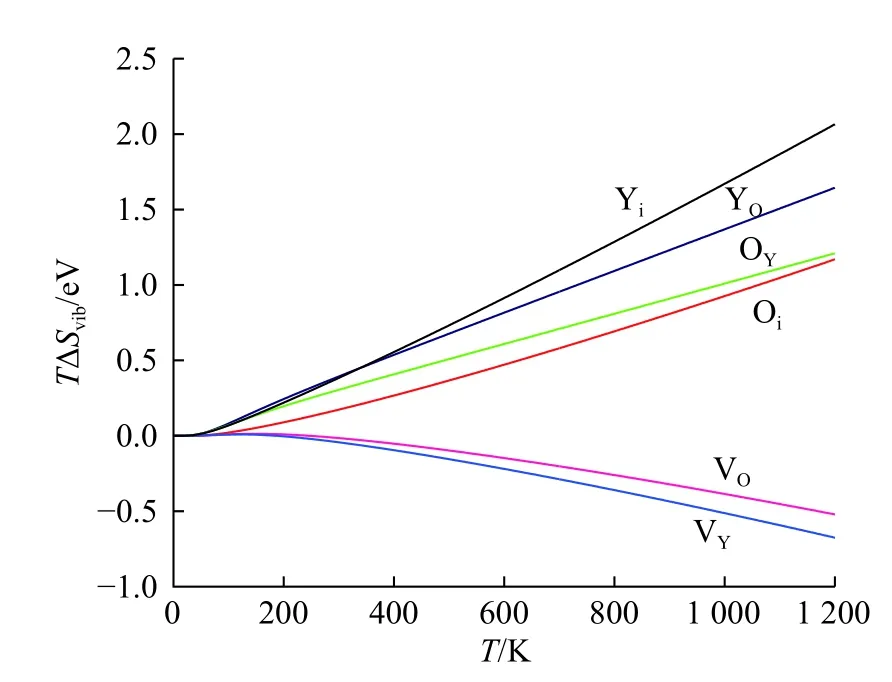
图2 不同缺陷的振动熵(TΔSvib)随温度的变化Fig.2 Vibration entropy (TΔSvib) of different defects with the change of temperature
2.3 热力学跃迁能级
热力学跃迁能级ε(q1/q2)描述的是同一类型的缺陷带不同电量、具有相同的缺陷形成能时所对应的费米能级。
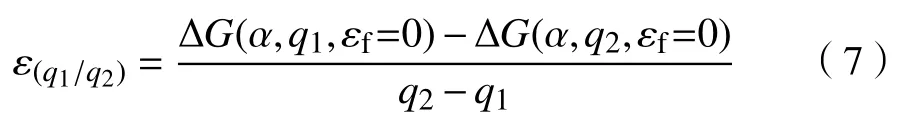
式中:原子类型为α;q1,q2为电荷。


图3 氧化钇本征点缺陷的热力学跃迁能级示意图Fig.3 Schmatic diagram of the thermodynamics defect transition levels of Y2O3 crystal
2.4 缺陷形成能
在研究氧化钇的缺陷形成能时,温度和氧偏压作为自变量,任意改变其中一个变量时,材料的缺陷形成能随之改变,组合出不同的变化规律。图4 是在选取3 种典型温度:300,800,1 200 K,及3 种不同的氧偏压:p(O2)=103Pa,p(O2)=10-3Pa,p(O2)=10-9Pa 后,经过排列组合后得出的9 种不同的环境状态。其中,横图代表相同温度下,改变氧偏压为103,10-3,10-9Pa 的情形。纵图代表相同氧偏压条件下,温度分别为300,800,1 200 K 的情形。在考虑了振动熵修正后的缺陷形成能示意图如图4 所示。

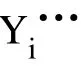


图4 在考虑振动熵影响后氧化钇的点缺陷形成能变化示意图Fig.4 Schematic diagram of the point defect formation energy of Y2O3 considering the influence of vibration entropy

图5 不同费米能级下最稳定的本征缺陷与温度和氧偏压之间的二维关联图Fig.5 Two-dimensional diagram of the most stable intrinsic defect under varying temperature and oxygen partial pressure at different Fermi levels

图6 本征点缺陷形成能随氧偏压、温度、费米能级变化的三维分布图(空间被划分成4 个区域)Fig. 6 Three-dimensional diagram of intrinsic point defect formation according to the oxygen partial pressure,temperature, and Fermi level (The space is divided into four regions)

3 结 论
基于第一性原理计算软件VASP 和晶格动力学软件GULP 研究了氧化钇(Y2O3)本征点缺陷的基本性质,在考虑振动熵以及环境条件温度、氧偏压的情况下,可得出结论:
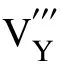

c. 制备氧化钇时,若要排除氧空位缺陷对晶体本身的影响,应采用高温或低氧偏压的环境,以适合晶体的生长。
