土塞对管桩纵向振动的影响研究及试验分析

(苏州科技大学土木工程学院， 江苏苏州215011)

0 引言

近年来，管桩由于制作成本低、承担荷载能力显著而被大规模应用于工程项目之中，其受力特性也受到了越来越多学者的关注。目前，管桩的研究主要集中在静荷载作用方面。如CROUSE等[1-2]进行了管桩的水平荷载试验并得到了不同工况下的p-y曲线。RANDOLPH等[3-4]依托实际工程，主要研究了静荷载作用下土塞对管桩承载力的影响，并通过数值模拟进行了验证。王家全等[5]通过管桩静压试验探究了土塞形成机理。张忠苗等[6]采用室内压桩试验得到了管桩土塞闭塞程度与土层的关系。贾媛媛等[7]采用有限元模拟的方法研究了管桩静载试验过程中桩的相关参数对管桩承载力的影响。而目前动荷载下管桩特性的研究尚处在起步阶段。刘林超等[8]将桩周土视作饱和土研究了管桩的水平振动。应跃龙等[9]将桩周土对管桩的作用视作动摩擦展开了饱和粘弹性地基土中管桩的纵向振动研究。翟志明等[10]研究了桩周土存在施工扰动时桩顶动力响应的理论解。王士革等[11]将桩周土视作分数阶粘弹性土研究了管桩的纵向振动。郑长杰等[12]将桩周土视作横观各向同性地基研究了管桩的扭转问题。针对管桩的一系列研究中，开口管桩中土塞的影响是个难点，一些学者开始展开针对土塞的研究。当前大多数研究都采用十分简单的接触模型来模拟管桩与土塞的接触作用，如李琪等[13]将土塞视作刚塑体进行理论推导，并结合实际算例验证了管桩的闭塞效应。刘林超等[14]将土塞—管桩—桩周土视作一个整体得到管桩的纵向振动方程并借助数值算例与欧拉模型进行对比。但是在实际情况下，土塞会随着管桩的入土深度而发生变化，所以将土塞—管桩视作一个整体会引起较大的误差。于是许多学者又开展了土塞—管桩接触面模型的研究。刘林超等[15]将土塞与管桩的接触视为Winkler弹簧和阻尼器并结合公式进行推导求得了管桩纵向振动理论解。吴文兵等[16]将土塞与管桩的接触视为分布式Voigt模型从而求解管桩的纵向振动。在这些研究中，不管是哪种土塞模型，都无法直接跟土体性质关联，需要凭借经验给出土塞作用参数。因此，更加合理的土塞计算模型研究亟待开展。

鉴于以上分析，虽然针对管桩的动力研究已有一些，但是考虑土塞的管桩模型的研究还很薄弱，本文将根据振动求解得出土塞振动复刚度，展开土塞—管桩耦合振动研究，并采用试验加以验证。

图1 数学模型Fig.1 Model of saturated soil-pile interaction

1 数学模型与基本假定

在轴对称条件下，考虑桩底土扩散效应时，对非均质饱和土—管桩—土塞的纵向振动进行研究，其基本模型如图1所示。管桩的长度为H，外半径为r1，内半径为r2，管桩桩底面以下的土层视为扩散虚土桩，长H′。将扩散虚土桩沿纵向分为k层，管桩纵向不分层，假设桩段为第m层，则m=k+1。最外层的土体径向无限大为外部区域。受桩施工影响产生的扰动的区域称为内部区域，将该范围的土体沿半径方向分成n个圈层，每个圈层土体性质一样，土层间的作用通过相邻圈层间剪切复刚度传递。

所建模型基本假定如下：

① 等截面管桩的材料为粘弹性；

② 虚土桩各段接触面及管桩与虚土桩接触面的位移和力保持连续；

③ 管桩、虚土桩与桩周土应力、位移连续，桩土振动为小应变振动。

2 饱和土体的动力响应

根据饱和介质理论和Novak的假设[17]可以求得j圈层的饱和土体动力平衡方程：

(1)

(2)

式中：

解方程(2)得：

(3)

式中：I0为零阶的第一类Bessel表达式，K0为零阶的第二类Bessel表达式。Aj和Bj分别为待求复系数。

外部区域(j→n)由于土体在无限远处没有位移，即Bn=0，所以：

(4)

(5)

设未扰动区域与受扰动区域交界面的剪切复刚度Kn为已知，则受扰动区域j圈层的复刚度：

(6)

其中：

(7)

利用式(6)、(7)并采用递推法即可得出径向非均质土体内部区域任一点的竖向剪切复刚度。

依据同样的理论，土塞与管桩交界面垂直向复刚度为：

(8)

式中：

3 管桩动力响应

以下是虚土桩及管桩沿垂直向振动的不同表达式：

虚土桩：

(9)

管桩：

(10)

桩顶边界条件为：

(11)

桩底边界条件为：

u1(x,t)|x=H+H′=0。

(12)

初始条件：

(13)

连续条件：

ui(x,t)|x=hi=ui+1(x,t)|x=hi，

(14)

(15)

对式(9)进行拉普拉斯变换得：

(16)

式中：

(17)

解式(16)得：

Ui(x,s)=Cicosλix+Disinλix，

(18)

式中：s=iω，Ci和Di为由边界条件确定的复常数。虚土桩底端不产生位移，则：

Zp0=∞。

(19)

根据位移阻抗的概念可以推导出虚土桩底部的阻抗表达式：

(20)

令：

(21)

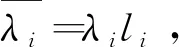
令h1=H+H′-l1,则虚土桩第一部分顶端的位移阻抗函数为：

(22)

式中：

因为虚土桩各桩段间速度、应力和位移都是连续的，所以相邻虚土桩截面间的位移阻抗是相等的，由相邻虚土桩关系的递推可得虚土桩顶部函数为：

(23)

式中:

Zp(k-1)可以通过阻抗函数的递推获得，把虚土桩的顶部力平均分配到管桩的底面上，则：

依据最初给出的条件，对式(10)进行相同的变换，对于没有土塞的管桩段，取K2=0,从而得到管桩顶部的阻抗函数

(24)

式中：

(25)

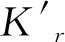
1.2.1 一般资料调查 建立护士应急人力调配使用表登记:包括日期、时间、求援科室名称、求援原因、调配方式(系统内、区域内)增援科室名称、增援护士姓名、到岗及结束增援的日期与时间。由科研组员4名科护士长负责区域内人力调配与登记及资料的收集。

桩顶速度频域响应函数：

(26)

对式(26)无量纲化：

(27)

桩顶位移频域响应函数：

(28)

对式(28)无量纲化：

(29)

当桩顶受到半正弦冲击力：

对q(t)进行拉普拉斯变化得：

(30)

则桩顶速度时域函数为：

V(t)=IFT[Q(ω)Hv(ω)]。

则桩顶无量纲时域函数为：

(31)

4 土塞影响分析

为明确开口管桩中土塞对其振动特性的影响，以下进行相关算例分析。未作特别强调，计算取值如下：管桩的外半径为0.3 m，内半径为0.2 m，长度为10 m，纵波波度为4 000 m/s，密度为2 500 kg/m3，弹性模量Ep=40 GPa,材料阻尼ηp=0；桩周土中土颗粒真实密度为2 500 kg/m3,阻尼比为0.05，土的渗透系数为6×107m/s。扩散虚土桩桩周土剪切波速为150 m/s；管桩土塞的剪切波速为120 m/s；脉冲宽度为0.8 ms。为突出反映土塞的作用，假设包裹管桩的土体纵向不分层。

4.1 土塞中水的体积分数与桩顶动力响应的关系

往砂土、粉土这些松散土地基中打入预制管桩，桩身土会受到挤压而逐渐密实，此时管桩周围的土体沿径向变得不均匀。假设此种情况下土的剪切波速由最外圈层的120 m/s按正比例增长到内部圈层的150 m/s，土塞高度为5 m。

图2表达的是土塞中水的体积分数与桩顶复刚度的关系，动刚度和动阻尼的振荡幅度都随着水的体积分数的上升而变大，但是增大的幅度不是太大。且在同一条曲线上，随着频率的变大，动刚度和动阻尼的振荡幅度也不断变大。

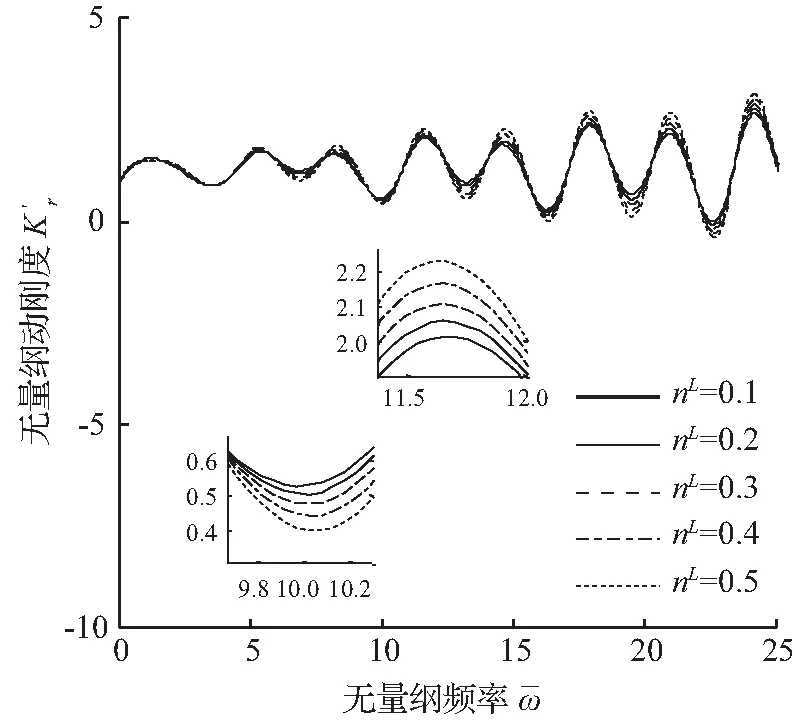
(a) 动刚度曲线

(b) 动阻尼曲线

图2 水的体积分数与复刚度的关系
Fig.2 Influence of water volume fraction on complex stiffness at top of pile

图3表达的是土塞中水的体积分数与桩顶速度响应的关系，从速度时域曲线可以看出，在土塞顶端(h=5 m)存在一个与入射方向相反的信号，且随着水的体积分数的不断增大，其幅值越来越小，这是由于水的体积分数越大，土塞就会越来越软，土塞与管桩的相互作用就越来越小，导致信号幅值不断减弱。伴随着水的体积分数的不断上升，桩顶同向反射的振幅不断加大。这是由于土塞中的水导致土塞变软，性质变差，吸收振动能量的能力减弱。由速度幅频曲线不难得出，随着水的体积分数的增加，相应曲线的振动幅度越来越大，但这些曲线振动幅度峰值所对应的频率基本不变。

(a) 速度时域曲线

(b) 速度幅频曲线

图3 水的体积分数与桩顶速度的关系
Fig.3 Influence of water volume fraction on velocity response at top of pile

图4表达的是土塞中水的体积分数与桩顶位移响应的关系，位移相频曲线显示了随着水的体积分数的增加，相应曲线的振动幅度越来越大，这是由于土塞性质变差引起的。但这些曲线振动幅度峰值所对应的频率是不变的。随着无量纲频率的增大，水的体积分数的影响很小。

(a) 位移相频曲线

(b) 位移幅频曲线

图4 水的体积分数与桩顶位移的关系
Fig.4 Influence of water volume fraction on displacement response at top of pile

4.2 土塞剪切波速与桩顶动力响应的关系

土塞高度为5 m，土塞的剪切波速分别为80、100、120、140、160 m/s。

图5表达的是土塞剪切波速与复刚度的关系，动刚度与动阻尼的振动程度均随着剪切波速的增加而减小，并且在同一剪切波速下，随着频率的增加，这两条曲线的振荡幅值均增加。这表明土塞剪切波速的变化对复刚度的影响不可忽略。

(a) 动刚度曲线

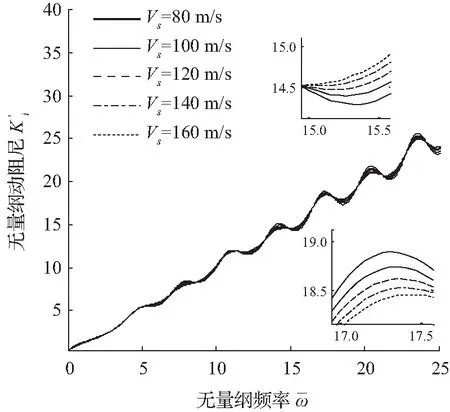
(b) 动阻尼曲线

图5 剪切波速与复刚度的关系
Fig.5 Influence of shear wave velocity on complex stiffness at top of pile

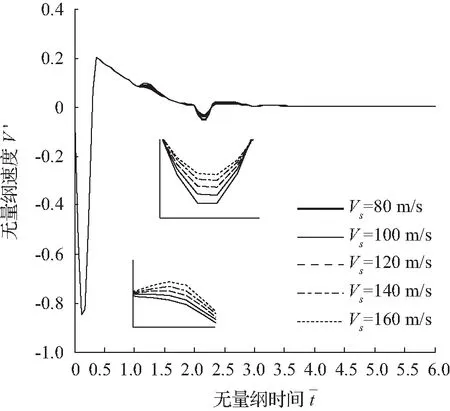
图6表达的是土塞剪切波速与速度响应的关系，由速度时域曲线可以看出在土塞顶端(h=5m)会有一个与入射方向相反的信号，且随着剪切波速的增加，其振荡峰值也越来越大，这是因为土塞的性质随着剪切波速的增加而变好，所以反向反射也就越明显，并且土塞能消耗更多从桩顶传下的能量，导致桩顶同向反射的振幅也随之减小。从速度幅频曲线可以得到随着剪切波速的增加，其振荡幅值越来越小，这也表明土塞性质越来越好。

(a) 速度时域曲线

(b) 速度幅频曲线

图6 剪切波速与桩顶速度的关系
Fig.6 Influence of shear wave velocity on velocity response at top of pile

图7表达的是土塞剪切波速与桩顶位移的关系，位移相频曲线显示了随着剪切波速的增加，相应曲线的振动幅度越来越小，但振动幅度峰值对应的频率是不变的。土塞中剪切波速变化对位移幅频曲线有一定影响，但是随着频率的增大影响变小。

(a) 位移相频曲线

(b) 位移幅频曲线

图7 剪切波速与桩顶位移的关系
Fig.7 Influence of shear wave velocity on displacement response at top of pile

4.3 土塞高度与桩顶动力响应的关系

本节分析在其他参数不变的前提下，土塞高度分别为0、2、4、8、10 m。

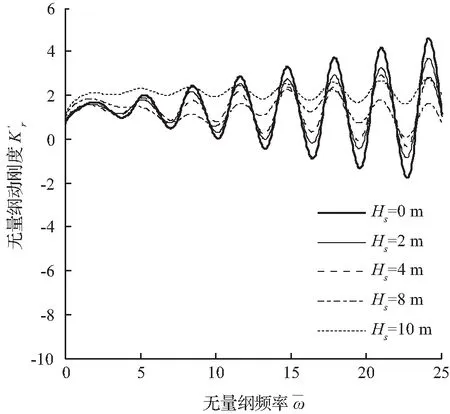
图8表达的是不同高度的土塞与桩顶复刚度的关系，动刚度曲线表明土塞高度越高，曲线振荡幅值越小，当整个桩段都是土塞时，动刚度曲线在低频段基本没有振动。动阻尼曲线表明，随着土塞高度的增大，其同一频率的振荡幅度越来越小，当整个桩段都是土塞时，动阻尼图像类似于一根过原点的倾斜直线。这表明土塞高度对桩顶复刚度的影响很大。

(a) 动刚度曲线

(b) 动阻尼曲线

图8 不同高度土塞与复刚度的关系
Fig.8 Influence of height of soil plug on complex stiffness at top of pile

图9表达的是不同高度的土塞与桩顶速度的关系，由速度时域曲线可以发现同向反射的振幅随着土塞高度的增加而变小，当土体进入管桩内部时，在同向反射之前会有一个反向反射出现，出现的位置与土塞到管桩顶面的长度有关。速度幅频曲线表明管桩中没有土塞的时候，曲线振荡很稳定，在整个桩段都是土塞时，曲线在无量纲频率较低处并未出现波峰。当土塞高度变大时，曲线的振荡不断变小。这是因为土塞高度越高，就会有更多的能量通过土塞消散，从而导致幅值越来越小。

(a) 速度时域曲线

(b) 速度幅频曲线

图9 不同高度土塞与桩顶速度的关系
Fig.9 Influence of height of soil plug on velocity response at top of pile

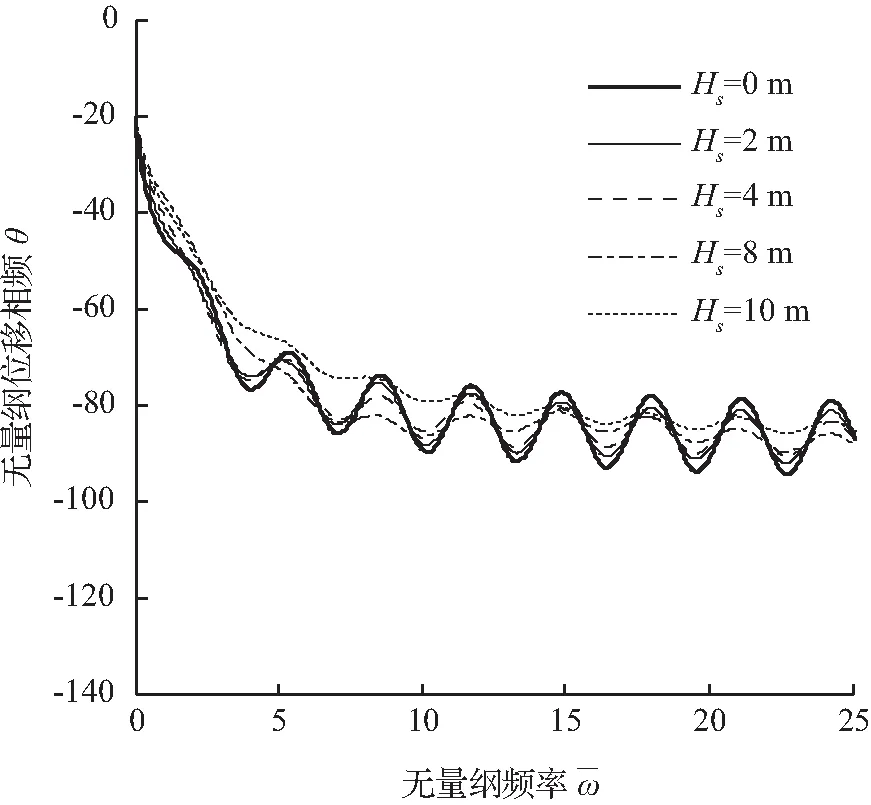
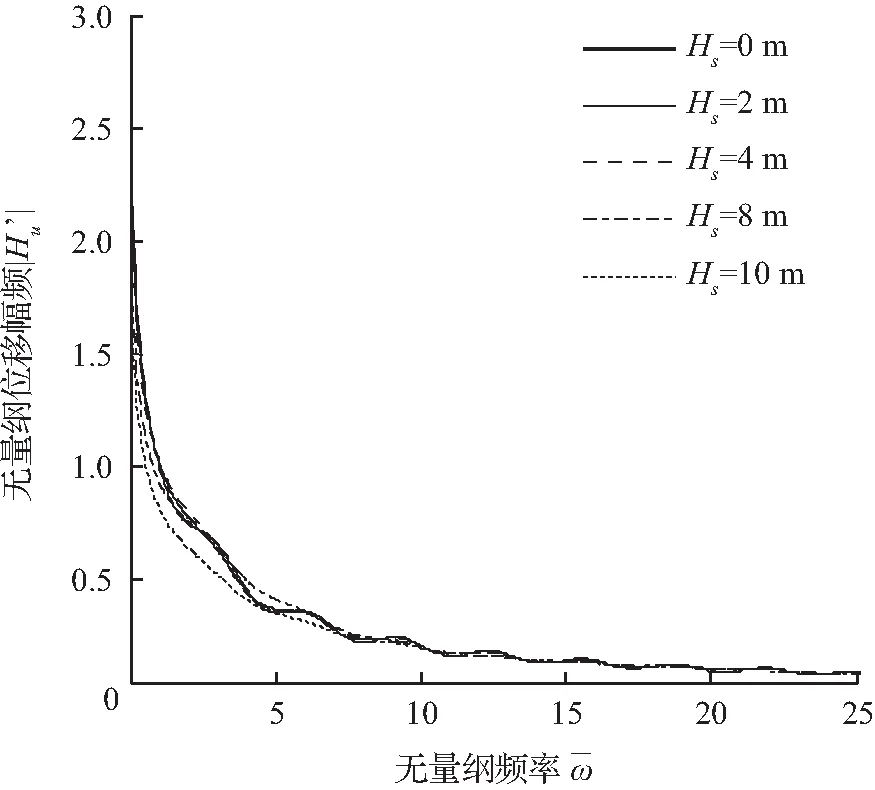
图10表达的是不同高度的土塞与位移响应的关系。位移相频曲线表明，当土体没有进入管桩内部时，曲线表现为等间距、等幅值的振动，曲线振幅随着土塞高度的增加而变小，当整个桩段都是土塞时，曲线基本无振动。位移幅频曲线表明曲线振荡随着土塞高度的增加而减小，当整个管桩段都是土塞时，曲线基本无振荡并且有下压的趋势，在低频阶段，位移幅频曲线的差异比较明显。

(a) 位移相频曲线

(b) 位移幅频曲线

图10 不同高度土塞与桩顶位移的关系
Fig.10 Influence of height of soil plug on displacement response at top of pile

5 室内模型桩试验

以上内容都是通过理论推导得出的结论，至于现实情况下桩顶动力响应是否符合以上变化还不能确定，所以本节采用室内模型试验验证以上理论结果的合理性。

试验材料：试验模型采用C25混凝土管桩，外半径为50 mm,内半径为25 mm。长度为1 m，密度2 200 kg/m3。桩周土及土塞用充分浸水的黄沙进行代替，密度为2 178 kg/m3。

试验设备：金属振动槽(半径0.3 m,高1.5 m)、EPPDS基桩低应变测试仪。

试验过程：首先将20 cm厚的淤泥质土埋设在金属震动槽底部，此土模拟的是虚土桩，接着用饱和黄沙来模拟桩周土，且黄沙分层压实分层饱和。接着将混凝土桩打入金属震动槽中，当桩头与桩周沙齐平时停止打入。

安装仪器进行管桩敲击试验。在敲桩之前，应先对动测仪中的相关参数进行设置，接着将传感器固定在管桩桩顶处，接着根据信号接收器的指示灯颜色变化进行采样，当指示灯颜色为红色时，用敲击锤敲击管桩顶部进行一次采样，电脑中所得的图像即为顶部速度时域图像。分别对管桩中土塞高为0、0.4、 0.8、1 m这四种情况进行敲桩观测，如图11所示。

(a) 土塞高度为0 m

(b) 土塞高度为0.4 m

(c) 土塞高度为0.8 m

(d) 土塞高度为1 m

图12 管桩波速测试图Fig.12 Test chart of wave velocity of pipe pile

经过数次重复计算，让试验所得图像与模拟结果的入射信号幅值以及第一次桩底反射信号幅值相等，就可以推算出试验所用沙的剪切波速Vs=105 m/s，接收器的脉冲宽度T0=0.4 ms。管桩中无土塞时的对比图如图13所示。

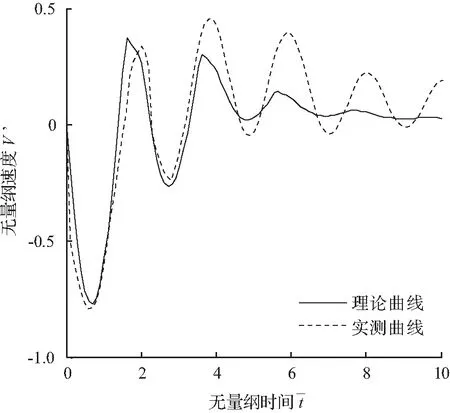
图13 管桩无土塞时理论与试验对比情况Fig.13 Comparison between experimental curves and theoretical curves of pipe pile without soil plug

把推算出的外侧沙的剪切波速以及脉冲宽度作为已知量，则可以求得土塞高度为0.4 m、0.8 m和1 m三种情况的理论解析式中的理论解，接着分别就这三种情况进行敲桩试验得到试验解，最后将理论解和试验解进行对比，对比情况如图14所示。

由图可以看出实测曲线在前期大体吻合，但在后期有较多振荡，这是由于所做的模型管桩长度比较短，且是用饱和砂土模拟的桩周饱和土，这时模型桩试验边界并不是理想状态。所以实测曲线振荡厉害的原因是模型试验边界以及试验误差的影响。随着土塞高度的增大，实测曲线的桩底第一次反射信号幅值越来越小，同样也可以验证前文理论推导的正确性。

(a) 土塞高度为0.4 m

(b) 土塞高度为0.8 m

(c) 土塞高度为1 m

6 结论

本文基于复刚度传递研究了考虑土塞效应时管桩纵向振动的定解问题，通过解析方法分别得到管桩桩顶复刚度函数、位移函数及速度函数。通过理论推导及试验得到以下结论。

① 土塞中水的体积分数越高，即土塞越来越软时，桩顶复刚度曲线、幅频曲线和位移曲线的振荡幅值越来越大，这是由于土塞不能很好的消散由桩顶传入的波导致的，且在土塞顶端会产生一个与入射方向相反的信号，但总体来说土塞中水的体积分数在高频段的影响比较小。

② 土塞剪切波速越大，即土塞性质越好时，桩顶复刚度曲线、幅频曲线和位移曲线的振荡幅值越来越小，且在土塞顶端会产生一个与入射方向相反的信号，剪切波速作为评判土质好坏的指标不应被忽略。

③ 土塞的高度越高，桩顶复刚度曲线、幅频曲线和位移曲线的振荡幅值越来越小，这是由于随着土塞高度的增加，土塞与管桩的接触面积也在增加，从而更容易消散桩顶传入的应力波。值得注意的是，速度时域曲线会有一个反向反射信号，位置与土塞距离管桩顶端的距离有关。

④ 试验部分表明本文的理论可以为工程实际提供一定的指导作用。