高宽比对连柱钢支撑框架结构抗震性能的影响
2020-05-29李锋赵宝成
李锋,赵宝成
(苏州科技大学江苏省结构工程重点实验室, 江苏苏州215011)
0 引言
采用传统抗震方法对结构进行设计,可以有效避免地震作用下建筑倒塌,为逃离建筑物赢得必要时间,保障了人员生命安全。但是地震破坏带来的经济损失和社会影响却依然十分巨大[1],如地震过后不少建筑损坏严重,则必须拆除重建;地震作用下损伤不严重的结构,加固和修复周期长和费用高,造成建筑使用功能中断,基于此对结构提出了新的抗震要求,以便实现建筑正常使用功能在短时间内的快速恢复。

图1 Pushover曲线Fig.1 Pushover curve
连柱框架( Linked Column Frame System, LCFS)是一种新型可更换构件的结构体系,设置并排柱并通过耗能连梁相连,利用耗能连梁的剪切或弯曲变形耗散地震能量,地震过后对耗能连梁进行更换,实现结构功能的快速恢复。近年来国内外学者对LCFS体系展开了系列研究。根据连柱体系侧向变形特点将其分为三个性能等级:弹性、快速恢复使用以及防倒塌(见图1)。通过控制层间位移大小对耗能连梁进行替换,能够快速恢复结构使用功能。陈以一等[2]进行了配置耗能连梁的复合高强钢框架的循环荷载试验,高强钢可以提高结构的抗震性能且震后的可恢复性能较好。
由于连柱钢框架结构主要依靠梁、柱承担水平荷载,抗侧刚度较小。为了广泛应用于高层建筑中,刘磊等[3]提出了连柱钢支撑框架结构,通过布置中心支撑提高结构的抗侧刚度,同时各层耗能连梁弹性塑性转角十分接近,耗能连梁塑性损伤沿高度分布均匀。
连柱钢支撑的柱脚与基础采用固定连接时,结构中可更换耗能连梁的损伤程度不大,原因是耗能连梁塑性变形通过连柱与框架柱同向弯曲变形时产生,塑性变形有限。虽然耗能连梁可采用低屈服钢材会优先进入弹塑性阶段,但是塑性发展程度不大。周颖等[4]对摇摆结构(Rocking Structure)进行了总结,通过放松上部结构和基础之间的约束,使结构与基础间仅有受压能力无受拉能力,地震作用下发生摆动,研究表明摇摆结构降低了上部结构的延性设计需求,减小了地震破坏,节约了上部结构造价。基于此思想,为了增加耗能连梁剪切变形,可考虑释放连柱柱脚竖向约束,即可抬起柱脚的连柱钢支撑框架结构体系(下文简称连柱钢支撑结构)。刘尚等[5]对柱脚可抬起的连柱体系进行了滞回性能分析,其破坏模式更为理想、结构损伤机制更加合理,耗能性能更好。但是耗能连梁布置在支撑框架之间的连柱上,耗能连梁竖向相对变形较小,进入塑性程度不够充分,为增加耗能连梁竖向相对变形,将耗能连梁布置在支撑两侧,在一个方向的水平荷载作用下,中间支撑框架的其中一个柱脚可抬起,反之亦然。
本文首先介绍了连柱钢支撑结构的特点;考虑竖向荷载作用,采用底部剪力法估算10层框架的侧向力大小,定量分析了小震和大震作用下水平倾覆力矩和竖向荷载抵抗矩的大小,以此评价高宽比对柱脚抬起的影响(仅考虑高宽比对支撑跨柱脚抬起的影响,所以高宽比指支撑跨的高宽比,非整体结构的高宽比);比较固接和可抬起两种不同形式柱脚对结构损伤程度和损伤分布形式的影响,提出了柱脚抬起高度的确定方法;同时依据上述方法,采用有限元软件ABAQUS建立了3层3跨,6层3跨和9层3跨连柱钢支撑结构有限元模型,着重分析高宽比对连柱钢支撑结构滞回性能的影响。
1 连柱钢支撑结构特点
图2为典型的连柱钢支撑结构,特点是连柱柱脚不能承受拉力,在罕遇作用下产生的水平倾覆力矩可能使一侧连柱柱脚向上抬起,并以另一侧连柱柱脚为“铰”转动,柱脚抬起一侧耗能连梁的塑性变形增加,框架部分的柱脚采用固接形式;支撑部分的柱脚通过放松基础和上部结构(连柱)间的约束,允许结构底部出现一定距离抬起,增加自身的摇摆,减小了强震下的主结构损伤和动力反应,可利用结构自重或预拉力来实现结构的回落和复位。
图3是一种可抬起柱脚的构造形式。底板与滚动轴承焊接,碟簧设置在底板上,通过螺栓连接将其固定。为了便于底板转动,底板上预留的螺栓孔按短槽孔设计[6]。比如,在向右的水平荷载作用下,左侧连柱会向上抬起,左侧连柱碟簧被压缩,左侧滚轴会随底板向上运动,离开基础预埋板,以右侧柱脚滚轴为支点转动,左侧连柱向上抬起的过程中,会伴随水平向右的微小移动,将螺栓孔设计为短槽孔后,可以减小螺栓杆和螺孔之间的磨损,避免出现柱脚下落时被倾斜螺栓卡住,无法正常回落。

图2 连柱钢支撑结构
Fig.2 Linked column steel braced frame

图3 带碟簧的可抬起柱脚
Fig.3 Lift column base with disc spring
2 模型设计及参数选取
2.1 结构模型设计
楼面恒荷载标准值为5.0 kN/m2,屋面恒荷载标准值为6.0 kN/m2,楼面活荷载标准值为2.0 kN/m2,屋面活荷载标准值为2.0 kN/m2,墙体材料重度为3.0 kN/m2,选用200 mm厚加气混凝土砌块,钢材密度7 850 kg/m3,楼板上荷载通过次梁以集中力的形式传递至主梁。抗震设防烈度为8度,基本地震加速度为(0.2g),设计地震分组为第一组,场地类别为Ⅱ类,抗震设防类别为丙类。
采用有限元分析软件SAP2000并参考偏心支撑的设计方法,设计并优化了3跨6榀10层连柱钢支撑框架,图4为平面布置方式,图5为②轴的立面布置图,表1给出了构件的详细尺寸。A、D轴线的柱为框架边柱(KBZ),B、C轴线的柱为中柱(KZZ),底部带“铰”的柱为连柱(ZKZ),与常规铰支座不同的是,此处“铰”可以向上运动,连柱和框架中柱间设置耗能连梁,A、B轴线间框架梁为KL1,支撑跨框架梁为KL2,ZC表示支撑框架中的支撑,LL表示耗能连梁,中柱和连柱之间轴线长度为1 350 mm,耗能连梁与柱翼缘采用高强螺栓连接,考虑耗能连梁端板厚度和柱横截面高度,1~3层耗能连梁长度为825 mm、4~6层为900 mm、7~10层为950 mm。下文建立有限元模型时对螺栓连接采用绑定连接简化。

表1 连柱钢支撑结构构件截面尺寸Tab.1 Dimension of component section of linked column steel braced frame

图4 连柱钢支撑框架平面布置
Fig.4 Plane layout of linked columnsteel braced frame

图5 10层3跨连柱钢支撑框架
Fig.5 3-span and 10-story linkedcolumn steel braced frame
2.2 分析参数选取
连柱钢支撑结构抗震性能优良,但在实际工程中连柱柱脚能否抬起、如何确定不同地震烈度下抬起的高度、柱脚的构造形式等问题需要详细研究。
首先需解决的问题是连柱柱脚能否抬起。MEEK[7]采用简化的单振型模型对不同高宽比的摇摆核心筒结构进行了分析,研究表明:摇摆核心筒可大幅减小结构的动力反应,且高宽比越大,动力反应减小效果越明显。YIM等[8-9]发现刚体的摇摆反应对体量、高宽比以及地震动类型非常敏感。以上分析均表明结构高宽比对结构摇摆反应有很大影响,本文选择高宽比作为分析参数,采用底部剪力法,定量分析了高宽比对连柱钢支撑结构柱脚抬起的影响。
3 高宽比对柱脚抬起的影响
3.1 水平地震作用分布
孙国华等[10]对钢板剪力墙结构地震倾覆力矩系数研究,发现随着结构层数的增加,高阶振型影响加剧,我国规范底部剪力法模式、振型分解法模式、弹塑性时程分析法的层剪力分布差异显著增大。但对于10层以下(高度小于40 m)的结构,底部剪力法与时程分析法的差异较小,可用来估算侧向力分布大小。
以支撑框架为分析对象,仅计算该支撑框架的水平地震力,不考虑边跨影响,对支撑框架柱脚计算倾覆力矩和总重力荷载代表值产生的抵抗矩。计支撑框架左、右柱间跨度为l,高度36 m,结构高宽比为36/l。
由式(1)和(2)计算结构基本自振周期T和多遇地震与罕遇地震的水平地震影响系数α1。
T=0.1n,
(1)
(2)
式中:Tg为特征周期,η2阻尼调整系数,αmax为地震影响系数最大值。
由式(3)和式(4)计算总水平地震作用标准值FEk和附加顶部集中力ΔFn:
FEk=α1Geq,
(3)
ΔFn=δnFEk,
(4)
式中:δn为顶部附加地震作用系数。
由式(5)和式(6)计算标准层和顶层水平地震作用标准值:
(5)
(6)

(7)
(8)
3.2 结构高宽比的影响
地震倾覆力矩为:
(9)
多遇地震下:FEk1=27.99l+100.27(11),罕遇地震下:FEk2=157.8l+565.1(12),取总重力荷载代表值计算重力抵抗矩:
(10)
下面分别讨论多遇地震和罕遇地震下两种力矩大小。多遇地震下:令ME>MR,经迭代计算,有l<3.27 m,此时结构高宽比为11.01。当高宽比大于11.01时,地震倾覆力矩大于重力抵抗矩,柱脚会向上抬起,反之不会。罕遇地震下:令ME>MR,有l<18.7 m,对应结构高宽比为1.93,当高宽比大于1.93,柱脚能够抬起。
通过估算发现:①在多遇地震作用下连柱钢支撑结构支撑柱脚不会抬起,耗能连梁变形较小,主体结构保持弹性。但是罕遇地震作用下侧向倾覆力矩明显增加,柱脚发生抬起,耗能连梁塑性变形较大,耗散地震能量增多,结构阻尼增加。②结构高宽比对连柱钢支撑结构影响较大,以上估算高宽比数值可为结构初步设计提供参考。
4 有限元模型建立与验证
4.1 钢材本构模型
有限元分析时,钢材本构模型采用双线型强化模型,单向加载时本构关系采用各向同性强化模型(Isotropic),循环加载下采用随动强化模型(Kinematic),采用Mises屈服准则,耗能连梁采用Q235B级钢材,其余构件均采用Q345B级钢材,钢材的弹性模量取为E=2.06×105MPa,泊松比μ=0.3,其余参数如表2所示。

表2 钢材性能参数Tab.2 Performance parameters of steel
注:表2中应力数值均已转换为有限元软件ABAQUS要求的真实应力,t为厚度,单位mm。
4.2 模型单元划分和边界条件
模型构件均采用shell单元,均选用4节点曲面壳(S4R)单元,采用结构划分网格法和进阶算法,可以得到较高质量的网格。
连接节点中,焊接截面均采用绑定接触(Tie)连接。约束框架梁上、下翼缘平面外的平动自由度(Uz)以防止面外失稳。耦合边柱各层在梁高范围区域到一点,作为水平荷载的加载点。在次梁传递集中力处,单独划分一区域并耦合至中心点,作为竖向加载点。边柱和中柱柱脚完全固接,连柱柱脚约束情况见下文。
4.3 模型加载制度
模型的加载分为两步:①分别在各层梁和柱上施加实际计算得到的竖向荷载;②在各层加载点处施加水平荷载。水平加载按倒三角分布,即一、二、三层水平荷载的比例在加载过程中始终保持为1∶2∶3。
为实现上述加载模式,引入基于多点位移控制的方法[11],在各水平加载点间建立位移约束方程:
∑(Pidi)-(∑Pi)d0=0,
(11)
式中:Pi是第i个加载点处施加荷载的比例系数;di是第i个加载点处的位移;d0是新增约束方程引入自由度的位移。
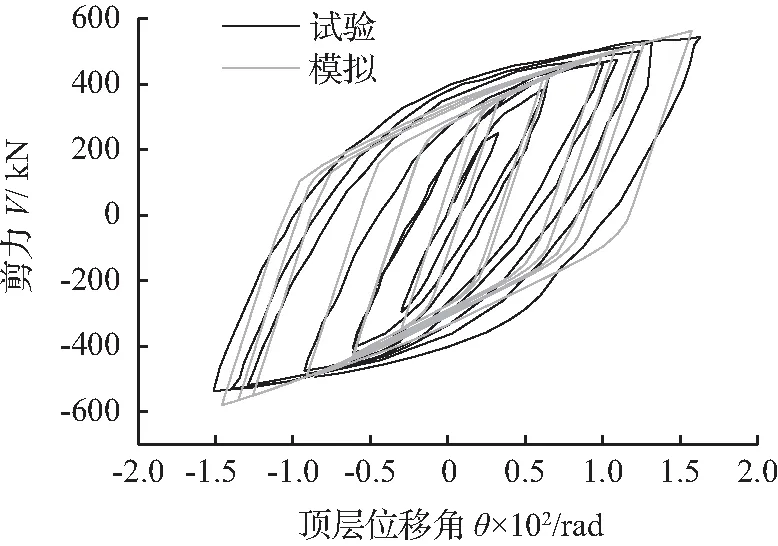
图6 K形偏心支撑试验滞回曲线对比Fig.6 Comparative hysteretic curves of K-eccentrically brace test
采用ECCS的完全加载制度,先分析得到有限元模型的单向水平加载曲线,由等能量法确定结构的显著屈服点[12],再施加以位移控制的水平往复荷载,按照Δy/4、Δy/2、3/4Δy、Δy、2Δy、3Δy……的方式进行,当位移小于Δy每级循环一次,当位移达到Δy每级循环两次,最大位移为框架侧移角达到0.02 rad。当承载力下降至最大值的85 %或耗能连梁以外的构件某一截面达到屈服应力,形成塑性铰,认为结构破坏。
4.4 试验验证
为保证本文有限元模型计算结果的可靠性,选取文献[13]中的K形偏心支撑钢框架试验进行验证。钢材材性、边界条件及加载模式均取自于试验,该钢框架共两层,跨度为1.9 m,层高为1.2 m。构件截面尺寸如下:柱截面为H150×150×7×10,梁截面为H150×150×7×10,支撑截面为H100×100×6×8,耗能连梁截面为H200×100×5.5×8,耗能连梁长度为300 mm,加劲板厚度均为6 mm。图6为试验及有限元模拟的滞回曲线。两种曲线吻合度较好,均呈现稳定、饱满的梭形,结构承载力较接近,说明本文采用的有限元分析方法可用于连柱钢支撑结构滞回性能研究。
5 连柱柱脚抬起高度确定
5.1 可抬起柱脚对损伤分布的影响
采用有限元软件ABAQUS按上述方法建立3层3跨连柱钢支撑结构模型,对比连柱柱脚固接和放松竖直向上(Uy)约束两种情况下的滞回曲线,评价可抬起柱脚对结构塑性损伤的影响。构件尺寸均采用表1,图7为有限元模型。
图8是两种形式柱脚的滞回曲线。固接形式柱脚对应的滞回曲线更加饱满,呈现梭形,抬起柱脚的滞回曲线呈现稳定的弓形。表3给出了整个加载过程中,结构累积滞回耗能和耗能连梁耗能情况,柱脚固接时,结构滞回曲线面积更大,耗能更多,但耗能连梁的耗能较少,主体结构会进入塑性,耗能连梁耗能占比仅为5.6 %,相比之下,柱脚可抬起时耗能连梁耗散的能量比例高达41.9 %,耗能连梁耗能充分。

图7 3层3跨连柱钢支撑结构模型
Fig.7 3-span and 3-story linked columnsteel braced frame model

图8 滞回曲线
Fig.8 Hysteresis curve
主要原因是,当柱脚可以向上运动,耗能连梁剪切变形增加,便于损伤集中在耗能连梁上,其它构件塑性发展程度很小,而柱脚固接时,主结构的梁、柱、支撑等构件均有不同程度的塑性损伤,没有严格的主、次结构之分,即能量分散到每个构件,结构整体耗能能力好,耗能连梁耗能能力有限,损伤程度小。

表3 耗能连梁耗能和结构累积滞回耗能Tab.3 Energy dissipation of link beams and structures
5.2 抬起高度的确定
由小变形假定,S=a×θp=e×γp,S为连柱柱脚竖向抬起高度,a为支撑跨轴线间距离,θp为结构顶层位移角,e为耗能连梁的长度,γp为极限状态时耗能连梁塑性变形角。对于抬起高度S的限值基于以下两方面考虑:
① 耗能连梁的变形能力。美国建筑钢结构抗震规范AISC的规定,剪切屈服型耗能连梁极限塑性转角γp=0.08 rad;弯曲屈服型耗能连梁极限塑性转角γp=0.02 rad。剪切型耗能连梁的耗能能力明显优于弯曲型,一般可按剪切型耗能连梁设计,故以0.08 rad为最大变形能力,以此作为确定柱脚抬起高度的一个约束条件。
② 结构水平位移角确定。我国抗震设防目标为“小震不坏,中震可修,大震不倒”。为实现此目标,连柱钢支撑结构设计理念是小震作用下结构基本保持弹性状态,中震作用下连柱柱脚向上抬起,结构有小幅度摇摆,耗能连梁优先耗能,保护主体结构,大震作用下约束柱脚竖向变形,支撑框架刚度增加,水平变形减小。以中震对应的顶层位移角θp为结构水平位移角上限计算抬起高度较合适。
黄悠越[14]认为钢筋混凝土框架结构层间位移角性能指标限值:完好0.004、轻微损坏0.005、轻~中等破坏0.009、中等破坏0.012、不严重破坏0.016。本文取0.01为位移角限值,并以此为确定柱脚抬起高度的另外一个约束条件。
连柱柱脚抬起高度取以上两种情况下较小值:
S=min{a×θp,e×γp}。
(12)
6 高宽比对连柱钢支撑结构抗震性能影响
类似摇摆结构,连柱钢支撑结构对高宽比敏感。本文利用有限元软件ABAQUS建立3层3跨、6层3跨和9层3跨,详细分析了高宽比的对该结构抗震性能的影响。
耗能连梁长度为e=850 mm<1.6Mp/Vp=869 mm,按剪切屈服型设计,连柱轴线间跨度为4 750 mm,抬起高度S=min{a×θp,e×γp}=min{4750/100,850×0.08}=47.5 mm,按此高度进行控制。
6.1 抬起柱脚模拟

图9 Spring2弹簧单元荷载和变形关系Fig.9 Load and deformation relation of Spring2 element
连柱柱脚被释放了部分约束,在有限元软件ABAQUS中选用Spring2单元代替,Spring2承受轴向荷载与变形关系由两部分组成,如图9所示,柱脚抬起高度不足47.5 mm,弹簧单元提供拉力很小,相当释放竖向约束,当抬起高度超过47.5 mm时,弹簧单元拉力骤增,实现竖向变形约束的效果。
6.2 有限元结果分析
6.2.1 破坏过程
限于文章篇幅,图10仅给出3层3跨模型正向加载时,顶层位移角达到0.005、0.010、0.015 rad的各构件塑性发展过程和屈服时序。图10(a)中耗能连梁最先屈服,塑性发展程度很大,其余梁、柱构件因采用Q345钢,屈服点高,仍处在弹性阶段。当位移增加至0.01 rad(注意图例最大值已由235 MPa换成345 MPa),此时左侧耗能连梁仍处于塑性阶段,左侧中柱节点及右侧框架边柱柱脚少部分达到屈服,其余部分依旧保持弹性状态。当位移增加至0.015 rad时,主结构塑性程度进一步发展,梁、柱和支撑应力明显增加,各节点处均有不同程度塑性损伤。从塑性损伤分布来看,顶层位移角达到0.01 rad之前,几乎集中在耗能连梁上,其他构件损伤程度很小,位移超越0.01 rad后,主结构才开始屈服并参与能量耗散。同时耗能连梁塑性损伤沿层高分较均匀。
6.2.2 滞回曲线
图11为模型的滞回曲线,纵坐标为基底剪力,横坐标为顶层梁的水平位移角,均呈现稳定的梭形,在弹性阶段,曲线包围面积都很小;位移增加结构进入快速恢复阶段,柱脚向上抬起,耗能连梁优先屈服,塑性损伤集中在可更换耗能连梁上,位移达0.01 rad左右,抬起柱脚柱脚被约束,曲线均有明显的“凹点”,基底剪力突增,支撑参与抵抗侧向力,结构承载力提高;此后结构进入防倒塌阶段,主结构开始进入塑性。同时随着高跨比的增加,结构的抗侧刚度降低,整体承载力呈下降趋势。

(a) 顶层位移角0.005 rad

(b) 顶层位移角0.010 rad
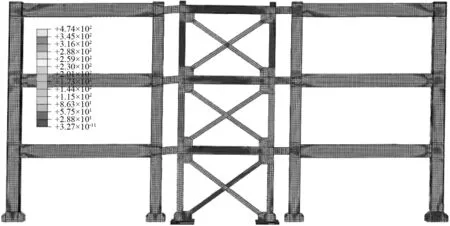
(c) 顶层位移角0.015 rad

(a) 3层3跨
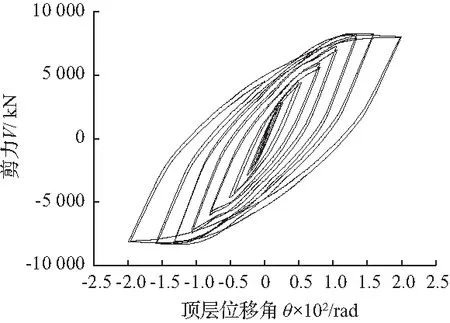
(c) 9层3跨
6.2.3 骨架曲线和刚度退化曲线
图12和13分别是3个模型的正向骨架曲线和刚度退化曲线。从图11中可发现,三条骨架曲线均呈现三阶段特性,顶层位移角0~0.003 rad为弹性阶段,0.003~0.011 rad为功能可恢复阶段,0.011~0.020 rad为防倒塌阶段。三个模型的最高承载力分别为12 546.6 kN、8 815.3 kN、8 291.9 kN,高宽比越大,承载能力越低,降低幅度为29.7 %和33.9 %。
图13表明,三个模型的初始抗侧刚度为167.7、72.4、45.3 kN/mm,最小抗侧刚度为54.9、20.5、12.5 kN/mm,刚度退化幅度分别为64.0 %、71.7 %、72.4 %,高宽比越大,降幅越多。其中3层3跨模型初始抗侧刚度最大,为6层3跨2.3倍、9层3跨的3.7倍,即高宽比越大,初始抗侧刚度越小。
6.2.4 耗能连梁替换范围
通过更换耗能连梁,可实现连柱钢支撑结构使用功能的快速恢复。依据骨架曲线的特征,利用等能量原理,确定替换耗能连梁对应的层间位移角。以图1中Vy1为替换范围的下限,Vy2为上限。表4给出了不同高宽比下替换范围的上、下限。由表4可以发现,虽然高宽比不同,但耗能连梁替换范围稳定在0.002 5~0.012 8 rad。

图12 骨架曲线
Fig.12 Skeleton curve

图13 刚度退化曲线
Fig.13 Stiffness degradation curve

表4 不同高宽比耗能连梁替换范围Tab.4 Replacement range of link beam with different aspect ratios
6.2.5 延性系数
延性系数采用下式计算:
(13)
其中:Δu为极限位移,Δy为结构屈服位移,按文献[12]方法计算。表5给出模型的延性系数,由于耗能连梁塑性发展很快,结构进入屈服时对应的位移角较小,但延性系数均大于4,表现出较好的整体变形能力,随着结构高宽比增加,延性也逐渐增大,表5中H为楼层层高3 600 mm。

表5 模型延性系数Tab.5 Ductility coefficient of model
7 结论
① 连柱钢支撑结构是抗震性能优良的功能可恢复结构体系,塑性损伤从耗能连梁开始发展,且主要集中可更换构件上,有效地保护了主体结构。
② 连柱钢支撑结构对地震烈度和结构高宽比较为敏感,罕遇地震下高宽比大于2.05的结构,地震倾覆力矩大于重力抵抗矩,连柱柱脚有抬起趋势。
③ 连柱柱脚抬起高度应根据结构水平位移角和耗能连梁的转动能力确定,取较小值。
④ 高宽比增加,连柱钢支撑结构承载力和抗侧刚度均有显著降低,延性和变形能力提高。但是正向骨架曲线均呈现明显的三阶段性能:弹性、功能可恢复和防倒塌阶段,通过替换损伤元件可实现结构功能快速恢复,建议层间位移角的范围为0.002 5~0.012 8 rad。
