基于易损性的RC桥墩复合损伤指标适用性分析
2020-05-29
(河北工程大学土木工程学院, 河北邯郸056038)
0 引言
桥梁作为重要的交通枢纽,如在地震等灾害中被破坏,将会对交通和灾后救援造成巨大影响[1]。基于以上考虑,桥梁结构的地震风险分析日益受到工程界的关注。其中,易损性分析能够预测不同水平的地震作用下结构发生各级破坏的概率,因此它在结构抗震设计和灾害评估中有重要价值和意义[2]。桥墩作为桥梁中极易受到破坏且不易更换的构件,其对桥梁结构的抗震性能具有重要作用。对其进行地震易损性分析,从宏观的角度描述地震动强度与结构破坏状态之间的关联性,可以为桥墩的抗震性能评估和维修加固提供工程依据。
近年来相关学者对桥墩易损性进行了研究。柳春光等[2]提出将墩顶漂移作为抗震性能量化指标进行易损性分析;HWANG等[3]提出了采用位移延性比定义桥梁墩柱的损伤;周长生等[4]用控制界面的曲率作为损伤指标分析圆形空心高墩的地震易损性;何浩祥等[5]阐述了通过对桥梁不同部位进行易损性分析进而实现综合损伤评定的策略,提出了基于多元模糊评定的桥梁地震易损性评价方法。传统的桥墩易损性分析中大部分单独把墩顶位移或曲率作为损伤指标,或者单独考虑桥墩的滞回耗能能力,而对于同时考虑墩顶位移和滞回耗能的复合损伤指标损伤研究较少。
为更准确描述桥墩屈服后性能,本研究提出基于墩顶位移和弹塑性耗能差率的复合损伤指标,用有限元软件OpenSees建立空心桥墩有限元模型,进行增量动力分析,并分别采用复合损伤指标、墩顶位移的损伤指标和弹塑性耗能差率的损伤指标作为损伤控制指标,建立空心桥墩的易损性曲线,探究复合损伤指标在空心矩形桥墩易损性分析中的适用性与有效性,并对某桥墩进行算例分析。
1 复合损伤指标的提出
1.1 既有的桥墩单一损伤模型介绍
1.1.1 基于墩顶位移的损伤指标
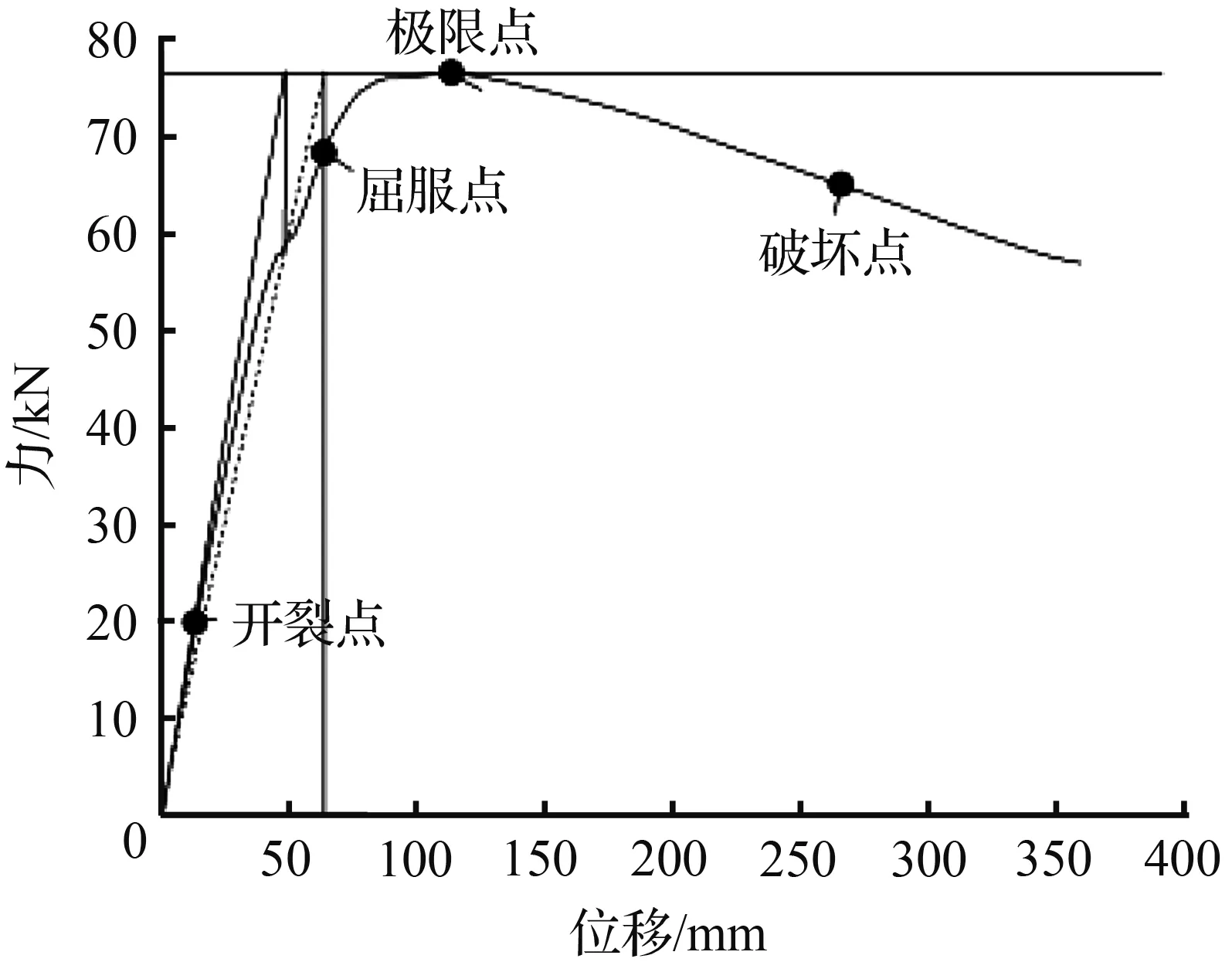
图1 模型力—位移曲线 Fig.1 Force-displacement curve of the model
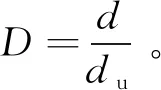

墩顶位移在一定程度上反映了桥墩刚度的影响,但以墩顶位移作为损伤指标忽略了桥墩滞回耗能的影响。

表1 墩顶位移指数不同损伤程度对应的损伤指数范围Tab.1 Damage index range corresponding to damage degree for pier top displacement index
1.1.2 基于弹塑性耗能差率的损伤指数

图2 弹塑性体系耗能示意图Fig.2 Energy dissipation of elastic-plastic system
弹塑性耗能差是以理想弹塑性体系发展来的。对于静力作用下的理想弹塑性体系,如图2所示,面积S0BCD为墩顶位移为um时产生的实际弹塑性变形能EF,面积S0AD为桥墩的理想弹性变形能EE,面积SABC为上述二者之差,称之为弹塑性耗能差ED。α为屈服后刚度与初始刚度之比。由此,文献[5]根据静力下的理想弹塑性体系,提出了基于弹塑性耗能差率的损伤指标。将该损伤指标应用到地震动作用下,提出基于弹塑性耗能差率的桥墩损伤评估方法。弹塑性耗能差率在一定程度上能反映屈服后耗能能力,但对结构屈服后刚度的影响考虑不足。
基于弹塑性耗能差的损伤指标可表示为
(1)
文献[5]建议的损伤程度对应的损伤指数见表2。

表2 不同损伤程度对应的损伤指数范围Tab.2 Damage index range corresponding to different damage degree
1.2 复合损伤指数的提出
由于单一损伤指标不能同时从位移和能量角度考虑桥墩损伤,因此本文根据既有的基于弹塑性耗能差率的损伤指标结合基于墩顶位移的位移损伤指标,提出一个考虑弹塑性耗能差和墩顶位移的复合损伤指标。即:
D=0.5(βDD+DF),
(2)
其中:DD为单独考虑墩顶位移的部分,DF为单独考虑滞回耗能差的部分。
由于基于位移的损伤指标和基于弹塑性耗能差指标在完全破坏(倒塌)时的下界限值不同,基于位移损伤指标的该界限值偏低,而基于耗能差损伤指标的该界限值较高,为保证两个指标的界限值一致,将基于位移的损伤指标进行调幅,使二者在完全破坏时的下界限值一致。具体计算过程如下:将DD乘以调幅系数β,β取基于弹塑性耗能差指标对应的倒塌时下界限值除以基于位移的损伤指标对应的倒塌时下界限值。
复合损伤指标的界线值即将单独考虑墩顶位移的部分的界限值和单独考虑滞回耗能差的部分的界限值带进(2)式中,可得复合损伤指标的界限值。复合损伤指标的划分范围见表3。

表3 复合损伤指数不同损伤程度对应的损伤指数范围Tab.3 Damage index range corresponding to different damage degree of composite damage index
2 损伤指标的适用性分析
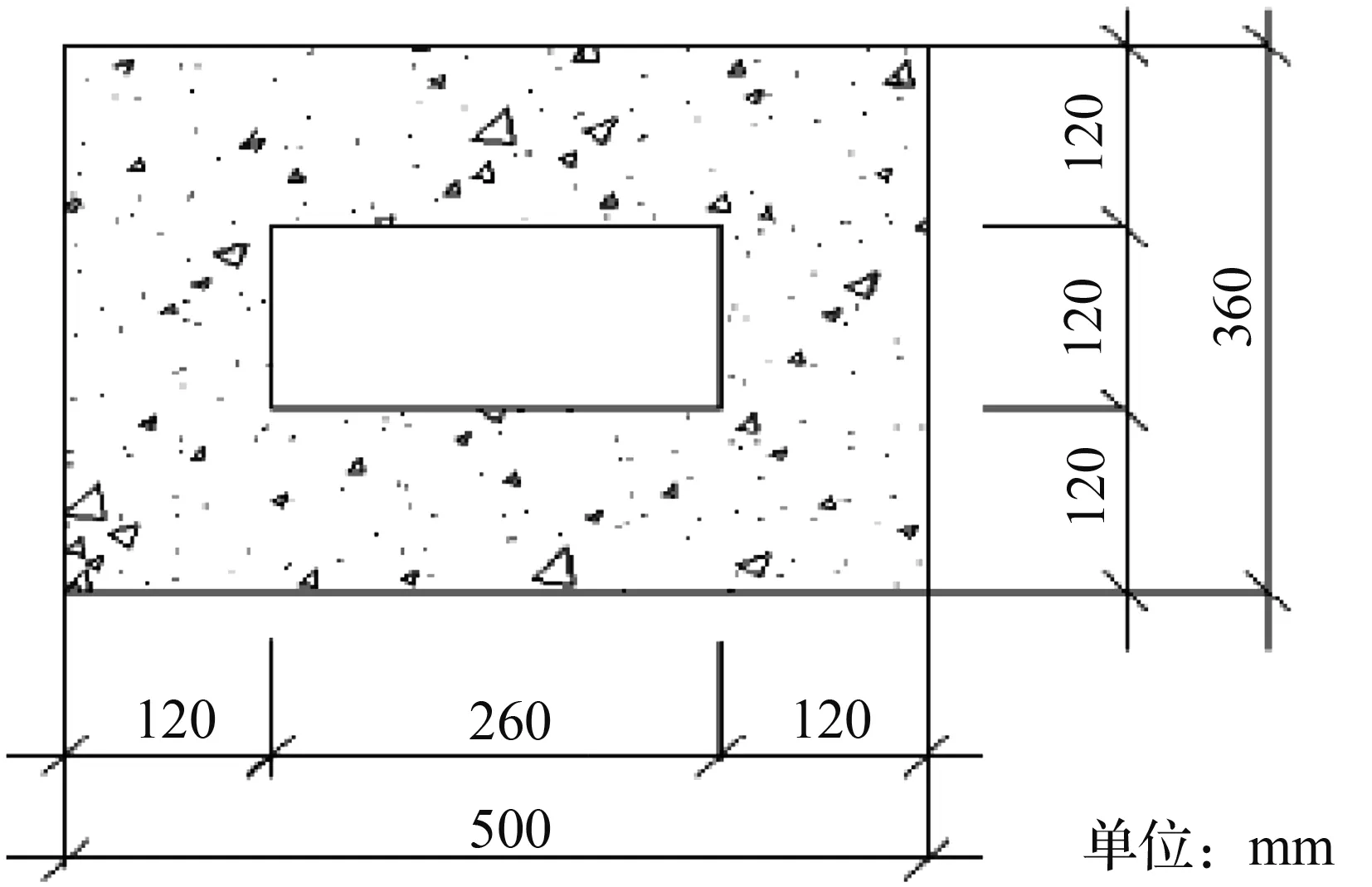
图3 桥墩截面几何尺寸Fig.3 Dimension of pier section
为了验证本文提出的复合损伤指标对空心桥墩的适用性和有效性,构建钢筋混凝土空心桥墩的数值模型进行分析。
2.1 空心桥墩验证模型
2.1.1 空心桥墩计算模型
为了保证有限元模型的合理性,本文选用河北工程大学张超等[9]论文中所确定的模型截面及配筋方式,模型的准确性和有效性已在本课题组论文[10]中进行了验证。本文的计算模型为墩高2.88m的矩形空心桥墩,桥墩截面几何尺寸见图3。其中,核心混凝土和保护层混凝土均采用C40,钢筋均为HRB335。模型其他参数见表4。

表4 模型设置参数Tab.4 Model setting parameters

图4 桥墩截面纤维划分Fig.4 Fiber section of pier section
2.1.2 OpenSees中桥墩模型参数的确定
纤维截面模型中,混凝土本构关系滞回模型取自OpenSees材料库中的Concrete02,即修正后的Kent-Park模型[11-13],这类材料考虑了混凝土的残余强度及线性拉伸软化。钢筋选取Giuffré-Menegotto-Pinto模型[14],考虑钢筋的屈曲、刚度退化,强度更接近实际受力情况。截面纤维划分如图4所示。利用有限元软件OpenSees建立空心矩形桥墩的弹塑性有限元分析模型。
2.1.3 地震波的选取
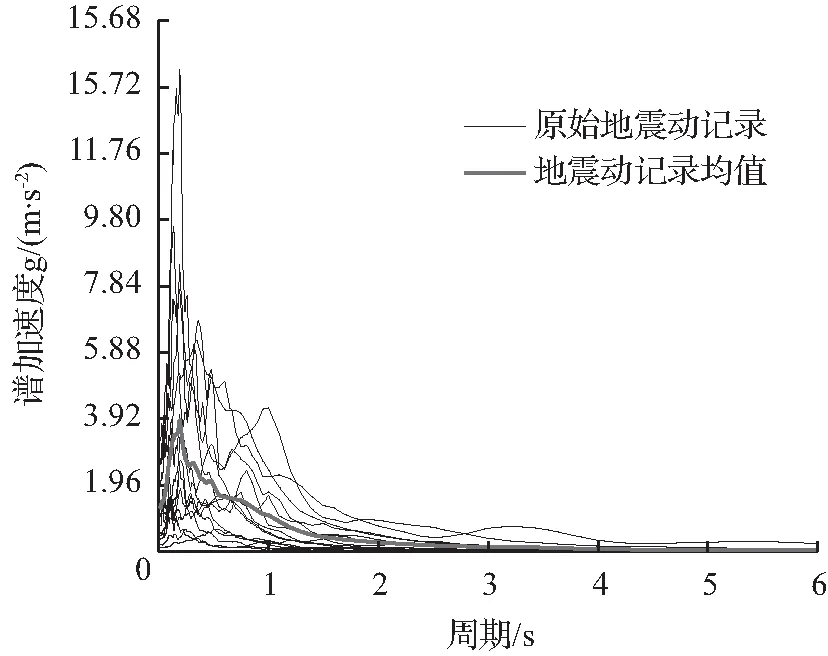
图5 地震反应谱 Fig.5 Response spectra of groundmotion records
研究表明:10—20条地震动记录进行增量动力分析可以得到较好的精度[15]。因此本研究从PEER(美国太平洋地震研究中心)中选取了15条适合于中国Ⅱ类场地、震级为5~8级的且震中距大于20 km的地震动记录。所选取地震波反应谱及其均值如图5所示。
2.2 计算结果及适用性分析
2.2.1 复合损伤指标损伤范围确定
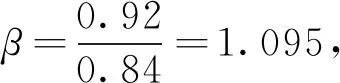

表5 基于墩顶位移损伤指数不同损伤程度对应的损伤指数范围Tab.5 Damage index range corresponding to damage degree of pier top displacement damage index

表6 复合损伤指数不同损伤程度对应的损伤指数范围Tab.6 Damage index range corresponding to different damage degree of composite damage index
2.2.2 地震需求参数回归分析
本文采用选取的15条地震波对桥墩进行IDA分析,以峰值地面加速度(gPGA)作为地震动强度指标,将15条地震动调幅成11个等级,分别为0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9、1.0、1.1、1.2 g。利用OpenSees将桥墩模型分别进行增量动力分析,得到矩形空心桥墩的需求响应。将数据进行线性回归,结果如图6所示,三种损伤指标的回归方程分别为:
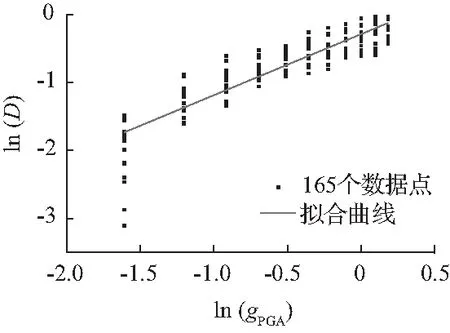
(a) 复合损伤指标的地震需求参数回归分析

(b) 基于弹塑性耗能差的地震需求参数回归分析
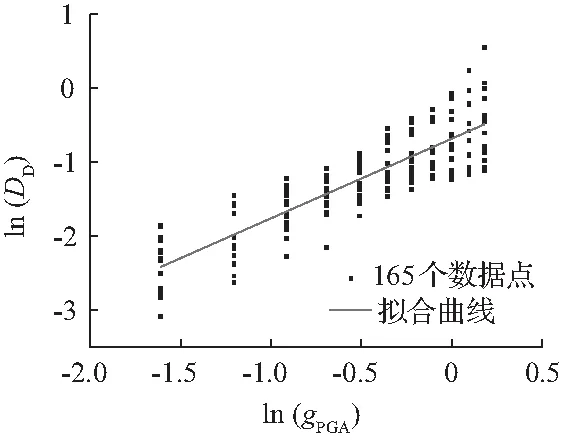
(c) 基于墩顶位移的地震需求参数回归分析
复合损伤指标的回归方程:
ln(D)=-0.284 37+0.900 09ln(gPGA);
(3)
基于弹塑性耗能差率指标的回归方程:
ln(DF)=-0.053 18+0.908 92ln(gPGA);
(4)
基于墩顶位移指标的回归方程:
ln(DD)=-0.683 23+1.079 75ln(gPGA)。
(5)
三种指标的拟合参数见表7。

表7 三种指标拟合参数对比Tab.7 Damage index range corresponding to different degree of damage
决定系数R2越接近1,说明拟合效果越好;而残差平方和越小,说明按最小二乘法理论拟合的曲线越好。通过比较,表明复合损伤指标的拟合效果更好,拟合优度更高。因此本文提出的考虑墩顶位移和弹塑性耗能的复合地震动参数有更好的适用性。
2.2.3 有效性分析
所提出的的损伤指标应该满足有效性,即损伤指数的标准差应该在小范围内波动,下面对两种损伤指标的标准差进行比较。由图7可以看出复合指标损伤指数的标准差最大不超过0.15,处于一个很小的波动范围,且在高PGA作用下复合损伤指标的精确度明显好于位移损伤指标,而基于墩顶位移的损伤指标波动很大,因此本文提出的考虑墩顶位移和弹塑性耗能差率的复合损伤指标具有有效性。
2.3 基于复合损伤指标的桥墩易损性分析
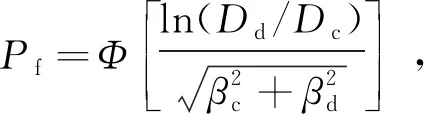

图7 标准差对比图
Fig.7 Standard deviation contrast diagram
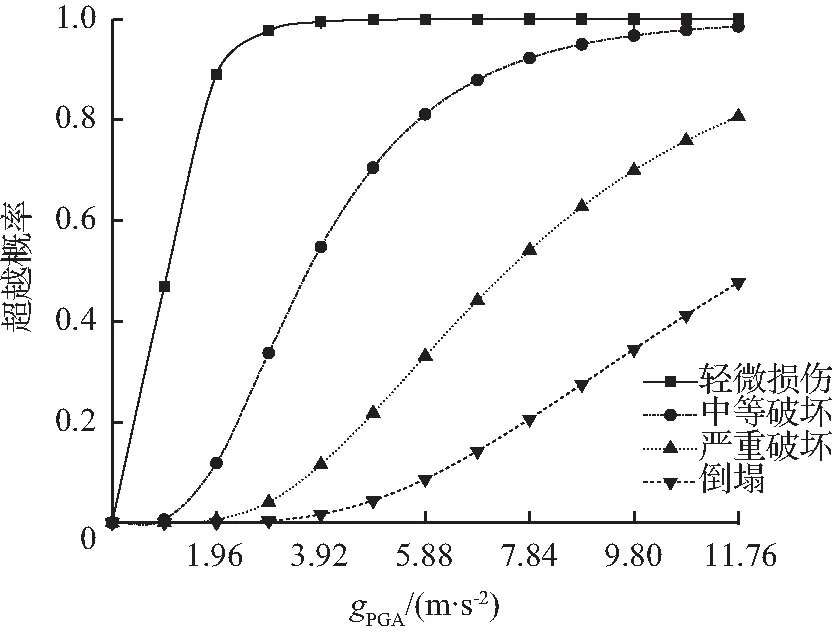
图8 复合损伤指标的易损性曲线
Fig.8 Vulnerability curve of composite damage index
通过易损性曲线可以判断某一gPGA值对应的破坏状态。如当gPGA=1.96 m/s2时,空心桥墩处于轻微损伤时的超越概率为89 %。当gPGA=11.76 m/s2时,桥墩处于完全破坏(倒塌)时的超越概率为48 %。以复合损伤指数作为损伤指标能从位移和能量的角度考虑空心桥墩的损伤情况,可以为空心桥墩的易损伤分析提供依据。
3 结论
本研究提出考虑墩顶位移和弹塑性耗能差率的复合损伤指标,并以某空心桥墩为模型,运用OpenSees建立数值模进行非线性增量动力分析,再分别用基于弹塑性耗能差率的损伤指标、基于墩顶位移的损伤指标和复合损伤指标进行线性回归分析,绘制易损性曲线,所得结论如下:
① 复合损伤指标既考虑了墩顶位移对桥墩损伤的影响,又能从滞回耗能的角度分析桥墩的损伤情况。因此本提出的复合损伤指标更加准确,更符合实际;
② 分别对基于弹塑性耗能差的损伤指标和复合损伤指标进行数据拟合,复合损伤指标的残差平方和更小,决定系数R2更高,表明用复合损伤参数进行桥墩损伤评估更具有适用性;
③ 本文提出的复合损伤指数的标准差波动范围很小,标准差最大不超过0.15,因此用复合损伤指标对空心桥墩进行评估具有有效性。运用复合损伤指标对空心桥墩进行易损性分析并绘制易损性曲线能够进一步为RC桥墩的损伤评估提供依据。
