交叉裂纹各裂尖应力强度因子同时快速求解的Williams单元
2020-05-29韩林君杨绿峰4
韩林君杨绿峰4
(1.广西大学土木建筑工程学院, 广西南宁530004;2.工程防灾与结构安全教育部重点实验室, 广西南宁530004;3.广西防灾减灾与工程安全重点实验室, 广西南宁530004;4.广西壮族自治区住房与城乡建设厅, 广西南宁530028)
0 引言
许多结构或结构构件,诸如航空航天工程、道路工程和房屋建筑工程等普遍存在裂纹缺陷,在外荷载作用下,裂纹极易扩展形成交叉裂纹。裂纹尖端应力—应变场的强弱程度通常采用应力强度因子(Stress Intensity Factors,简记为SIFs)来表征。传统的有限元法计算裂尖SIFs时需在裂尖人为确定奇异区尺寸,然后利用线性外推获得裂尖SIFs,然而多条裂纹交叉使得裂尖SIFs不再相互独立,将受各裂尖奇异区尺寸和间距等因素影响,很难同时快速准确获得各裂尖SIFs。因此,建立能够同时快速准确求解裂尖具有相关性的交叉裂纹各裂尖SIFs的算法,对含交叉裂纹结构安全评价具有重要意义。
外荷载作用下交叉裂纹受力较为复杂,目前主要采用数值算法进行模拟。章青等[1]提出了广义扩展有限元法,并基于此方法研究了交叉裂纹裂尖SIFs及其扩展路径;石路杨等[2]建立了求解多裂纹扩展的扩展有限元法,结合算例计算了含交叉裂纹体裂尖SIFs,并模拟了多裂纹扩展及交叉汇合过程;DUAX等[3]采用扩展有限元法研究了交叉裂纹裂尖SIFs,证明了该方法能够有效地解决交叉裂纹问题。然而采用扩展有限元法解决交叉裂纹问题时,需要在位移场中引入由交叉点产生的附加位移项,使位移场形式更为复杂。文献总结发现,简化为十字交叉的裂纹也备受关注。BROCK等[4]将十字形臂视为位错阵列,并将十字交叉裂纹受双向拉伸载荷问题简化为一对耦合的积分方程,进而研究其动态扩展;MOUSKOS等[5]采用解析函数理论和Busemann-Chaplygin技术,研究了平面应变情况下十字交叉裂纹的扩展问题;郭怀民等[6-7]采用复变函数法研究了不对称椭圆孔边裂纹问题和星形裂纹问题,通过改变几何参数,将问题蜕化为十字交叉裂纹问题,并给出了I型和II型裂尖SIFs的解析解;余敏等[8]采用弹性复势法研究了压电材料中非对称十字交叉裂纹反平面问题,并推导出了裂尖III型广义强度因子、能量释放率和应变能密度因子表达式;牛燚炜[9]基于广义粒子动力学法对含预制十字裂纹的岩石材料进行了二维和三维的数值模拟,得到预制裂纹对岩石材料的破坏机理和力学性能的影响;CHEN[10]给出了十字交叉裂纹问题的数值解法,得到了非等长正交十字裂纹裂尖SIFs,并与解析法结果进行了对比;李浪花[11]采用含十字交叉初始裂纹的试件研究了单向受力初始裂纹的起裂和扩展,并通过ABAQUS软件进行数值模拟以验证实验结果。
杨绿峰等[12-15]基于广义参数有限元法,研究建立了广义参数Williams单元(简记为W单元),目前已实现不同断裂模式下的单条裂纹和相互独立的多条裂纹裂尖SIFs的快速直接求解。本文结合广义参数有限元思想,研究建立了交叉裂纹各裂尖SIFs同时快速求解的W单元计算格式,因各裂尖之间不再相互独立,进一步分析了相关参数,如薄板尺寸、裂纹夹角与奇异区尺寸等对交叉裂纹各裂尖SIFs的影响。算例证明本文方法能同时求解交叉裂纹各裂尖SIFs,且具有较高的计算精度。
1 模型的建立及离散
如图1所示,为含多条裂纹且至少任意两条裂纹相交的交叉裂纹示意图,将模型的几何中心作为坐标原点o,水平方向为x轴,逆时针旋转90°为y轴,建立整体坐标系xoy;以裂尖i为例说明局部坐标系建立规则:将裂尖作为坐标原点oi,裂纹扩展方向为xi轴,逆时针旋转90°为yi轴,建立局部坐标系xioiyi,图1所示计算模型中含有z条裂纹,不考虑分支裂纹的情况,共有2z个裂尖,因此需建立2z个局部坐标系。
因裂尖应力具有奇异性,故将整个计算模型离散为裂尖奇异区和外围常规区。外围常规区可利用ANSYS有限元软件中8节点等参单元自动离散,减少前处理工作量。裂尖奇异区离散过程如下:选取以裂尖oi为中心点,边长为l的正方形区域为奇异区,将奇异区边界进行8等分离散,并分别与中心点oi连接,如图2所示。选取条元oiL1L2作为典型单元进行说明,利用一组环绕裂尖oi且相互平行的折线将条元划分为n层梯形微单元和红色裂尖三角形单元,n称为W单元内的径向离散单元数。任意相邻折线Γn、Γn-1到裂尖oi的距离之比为常数,称为奇异区径向离散比例因子α。W单元最外层微单元L1L2L3L4的边L1L2为常规区与奇异区的交界,其上3个黑色实心圆形表示常规单元节点,另外的5个空心圆形位于奇异区内,为虚节点,故称微单元L1L2L3L4为过渡单元。根据上述离散方式,可将任一裂尖奇异区等分为8个W单元。

图1 交叉裂纹示意图
Fig.1 Diagram of cross cracks

图2 裂尖奇异区离散示意图
Fig.2 Discretization element aroundthe crack tip in singular region
2 交叉裂纹各裂尖SIFs同时快速求解的W单元
2.1 整体位移场与局部位移场
以图1所示交叉裂纹任意裂尖i为例,裂尖奇异区整体位移场可用改进的Williams级数表示,并截取前m+1项,即:
(1)

(2)
式中:Ki,I、Ki,II分别为i裂尖的I型SIFs与II型SIFs。
将式(1)改写为矩阵相乘形式:
[ω]i=[F(r,θ)]iφi,
(3)
由于φi中的参数ai,j、bi,j是广义的,无具体物理意义,故称之为广义参数。裂尖奇异区的整体位移场由改进的Williams级数建立,由于裂尖三角形微单元较小,可忽略其对条元oiL1L2的贡献。故W单元为条元内n层互相似的梯形微单元的集合。
以奇异区内的任一梯形微单元为典型单元,根据有限单元法可得其梯形微单元局部位移场:
(4)

由总体位移场控制局部位移场求出各个结点的位移表达式,对于图2所示裂尖i周围的梯形单元有:
(5)


(6)

由式(4)和式(5),可得梯形微单元广义参数位移场:
(7)
2.2 建立单元刚度方程
由“2.1节”可知:整个模型离散为2种单元类型,即:奇异区W单元与外围常规区8节点等参单元,下面分别介绍这两种单元刚度形成过程。
2.2.1 奇异区W单元刚度方程
对于奇异区内任意第k层梯形微单元(2≤k≤n),根据变分原理,建立其常规单元刚度方程:
(8)

则第k层梯形单元的广义刚度方程可以表示为:
(9)

将条元内第2层到第n层单元的刚度进行叠加,得到条元奇异区刚度方程:
(10)

对于奇异区最外层的过渡单元,如图2所示,建立其常规单元刚度矩阵并分块表示为:
(11)

进而得到过渡单元广义刚度方程:
(12)

将式(10)和式(12)叠加,得到条元o1L1L2,即1个W单元的刚度方程:
(13)

根据式(13)集成单个裂尖8个W单元刚度方程:
(14)

2.2.2 外围常规区8节点等参单元刚度方程
根据有限单元法,常规单元刚度矩阵可由下式得到:
(15)

进行整体坐标与局部坐标转换时,有面积微元公式:
dxdy=|J|dξdη。
(16)
将单元刚度矩阵进行高斯计算可得到:
(17)
式中:Hi、Hj为高斯积分点权函数;N为高斯积分点数;|J|为雅可比行列式。
根据变分原理,建立上述交叉裂纹模型的常规区所有单元的刚度方程并进行集成,可分块表示为:
(18)
式中:下标r表示常规区内所有节点。
2.3 建立整体控制方程
根据2.2.1节与2.2.2节中建立的单个奇异区所有W单元和外围常规区所有8节点等参单元刚度方程。将2z个裂尖奇异区所有W单元刚度方程和常规区所有单元刚度方程进行集成,得到整个求解域内的整体控制方程:
(19)
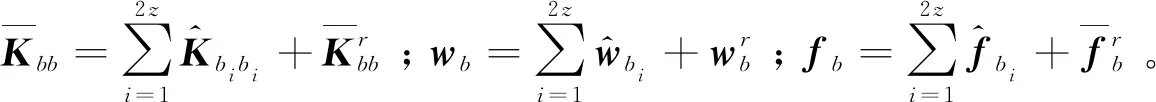
引入位移和应力边界条件,对整体控制方程进行求解,即可求得各裂尖奇异区的广义参数列阵φ1,φ2,…,φ2z,进而从各裂尖广义参数列阵中提取ai,1、bi,1,根据式(2)计算得到交叉裂纹各裂尖SIFs。
3 算例分析

图3 含中心交叉裂纹弹性薄板Fig.3 Elastic thin plate with cross cracks
本算例将图1所示的多条交叉裂纹模型简化为如图3所示的中心十字交叉裂纹矩形薄板。板宽为2W,高为2H,板厚为单位厚度,以十字交叉裂纹交点为坐标原点o,水平方向为x轴,逆时针旋转90°为y轴,建立整体坐标系xoy;将裂尖作为坐标原点oi,裂纹扩展方向为xi轴,逆时针旋转90°为yi轴,建立局部坐标系xioiyi(其中i=A,B,C,D,详见图3)。沿x轴水平裂纹长度为2a,过中心的斜裂纹长度为(b+c),其中b=e+d,c=e-d,e和d均为斜裂纹长度参数,裂纹夹角为γ;材料参数泊松比为μ,弹性模量为E;板边受平行于y轴和x轴的均布拉应力分别为σ和λσ作用,其中λ为荷载参数,表示板边平行于y轴和x轴所承受的拉应力比值。
采用本文方法计算十字交叉裂纹各裂尖SIFs时,裂尖奇异区采用W单元分析,外围常规区利用ANSYS有限元软件中8节点等参单元自动离散,并生成节点和单元信息文本作为本文方法FORTRAN95编程计算的前处理文件。由图3可知,根据十字交叉裂纹中两条裂纹的位置关系,可将其分为正交十字裂纹和斜十字裂纹。下面将以这两种情况进行研究:
3.1 正交十字裂纹
根据Ⅱ型裂纹的定义可知:因计算模型存在对称性,当承受对称荷载时,裂纹上下表面未发生相对滑移,故在本节研究中所有裂尖仅存在I型SIFs。
3.1.1 等长正交十字裂纹
取裂纹半长a=b=c=10 cm,裂纹夹角γ=90°,板边受平行于y轴和x轴的均布拉应力分别为σ和λσ作用,其中σ=1.0 kN/cm。由于模型与外部载荷均具有对称性,则有KI,A=KI,C,KI,B=KI,D。将本文方法计算结果与应力强度因子手册[16]解(见应力强度因子手册增订版95页):
(20)
作比较。
通过设置不同的W/a分析板的尺寸效应对裂尖SIFs的影响规律。由式(20)可知:裂尖SIFs与裂纹半长a、荷载参数λ及外荷载σ相关,故同时讨论了无限大板界限与荷载参数λ之间的关系。由图4可知,无论荷载参数λ如何取值,均在满足W/a≥13时,KI,A与KI,B皆稳定收敛于应力强度因子手册解,可以忽略板的尺寸对裂尖SIFs的影响,即可视为无限大板。当λ=0.5时,随着W/a的逐渐增大,KI,A呈现减小趋势,KI,B则呈现增大趋势;当λ=1.0时,板承受四边均布拉应力,即σ=λσ,所以KI,A=KI,B。随着W/a的逐渐增大,KI,A和KI,B均呈现减小趋势;当λ=2.0时,随着W/a的逐渐增大,KI,A呈现增大趋势,KI,B则呈现减小趋势。
同时以W/a=13为例,研究荷载参数λ与SIFs的关系,将本文方法计算结果与应力强度因子手册解进行对比分析,计算结果高度吻合,相对误差极小,如图5所示。随着荷载参数λ的逐渐增大,KI,A逐渐减小,KI,B逐渐增大,且呈线性规律变化,与应力强度因子手册解变化一致,验证了本文方法的正确性及高精性。

图4W/a与λ的关系
Fig.4 Relationship betweenW/aandλ

图5KI与λ的关系
Fig.5 Relationship betweenKIandλ
3.1.2 非等长正交十字裂纹
取裂纹半长a=15 cm,且有a≠b,d=0,通过改变裂纹长度参数e来改变裂纹半长b和c,进而改变式(21)中参数t的取值。选取板尺寸W=200 cm,H=13b,此时可将模型看作无限大板,取板厚为单位厚度,裂纹夹角γ=90°,板四周承受均布拉应力σ=λσ=1.0 kN/cm。将本文方法计算结果与应力强度因子手册解进行对比。其中应力强度因子手册解(见应力强度因子手册增订版95页)为:

图6 Origin拟合曲线Fig.6 Origin fitting curve
(21)
式中:t=a/(a+b);F(t)由应力强度因子手册查得。
将本文方法计算非等长正交十字裂纹裂尖SIFs的结果采用Origin软件进行多因素拟合分析,拟合曲线如图6所示,拟合曲线参数见图6中的表格,拟合得到计算表达式如下:
F(t)=5.595 22t4-12.026 71t3+
6.941 41t2+0.488 14t+0.011 78,
(22)
式中:t=a/(a+b)。
3.2 斜十字裂纹
斜十字裂纹作为十字交叉裂纹更为普遍的情况,研究其裂纹夹角、奇异区尺寸等对各裂尖SIFs的影响具有重要意义。以图3为基本计算模型,取裂纹长度b=e+d,c=e-d,其中e=a,裂纹夹角为γ,受双向均布拉应力σ=λσ=1.0 kN/cm。采用本文方法计算斜十字裂纹各裂尖SIFs,并将计算结果与应力强度因子手册解或ANSYS解进行对比分析。
根据小节3.1中对含垂直交叉裂纹薄板无限大板界限的判定,本节取板尺寸W=H=350 cm,板厚为单位厚度,水平裂纹半长a=20 cm,裂纹夹角γ=45°。分别取不同d值,讨论d/a对各裂尖SIFs的影响,对应的应力强度因子手册解为[16]:
(23)
式中:F由应力强度因子由手册查得。
本文方法计算结果如图7所示,应力强度因子手册解可由式(23)计算得到,将本文方法计算结果与应力强度因子手册解进行对比,对于I型和II型SIFs,相对误差均在5 %以内,需要说明:该应力强度因子手册解的修正系数由应力强度因子手册中曲线图进行取值,即本算例中应力强度因子手册解存在着人为误差。由图7可知,随着d/a的增大,KI,B、KI,C、KII,A和KII,B呈现逐渐增大的趋势,KI,A、KI,D和KII,C呈现逐渐减小的趋势,而KII,D则呈现先减小后增大的趋势。
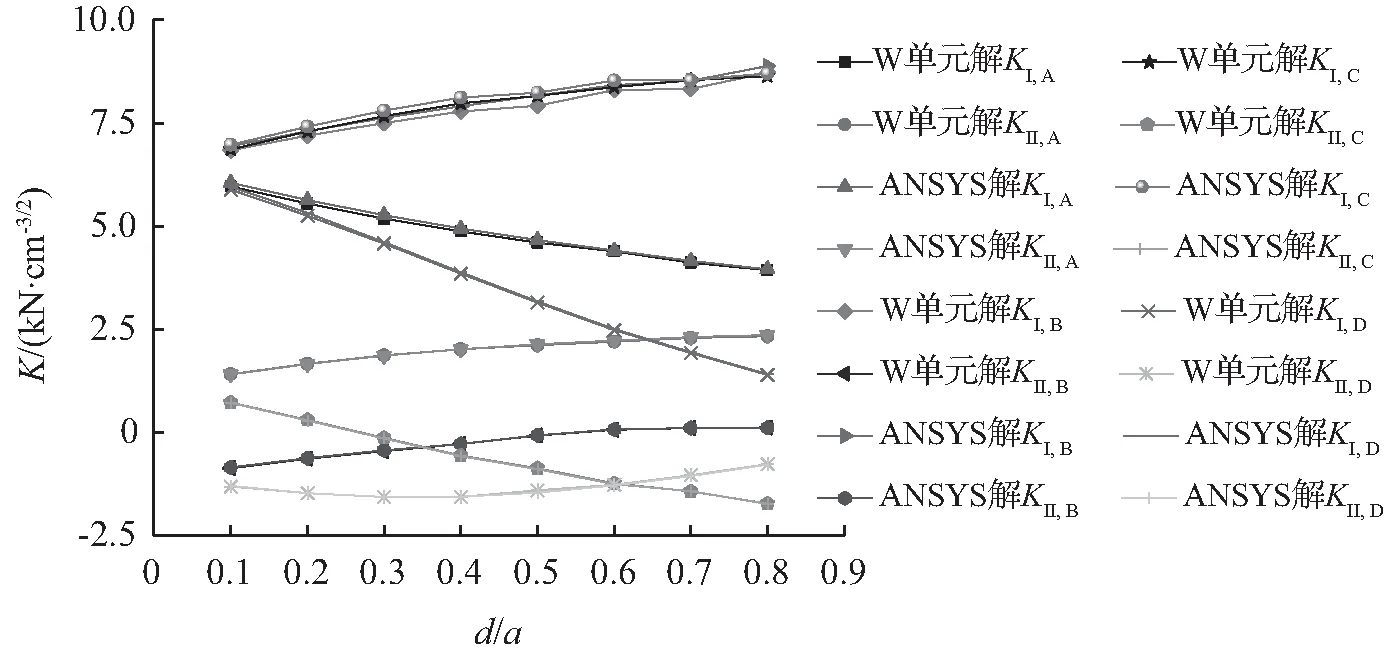
图7 各裂尖SIFs与d/a的关系Fig.7 Relationship between SIFs and d/a at each crack tip
需要注意的是:对比本文解与应力强度因子手册解可知,本文方法的计算结果与应力强度因子手册(增订版,97~98页)中对于C、D裂尖的II型SIFs系数的判定相悖,将手册解中C、D裂尖的II型SIFs系数相互调换可能为正确解。为此,本文采用ANSYS解进行佐证可得:应力强度因子手册(增订版,97~98页)中C、D裂尖的II型SIFs系数相互调换方为正确结论。
此外,本文分析了裂纹长度参数d=0时,不同裂纹夹角γ对裂尖SIFs的影响。使用本文方法分别计算裂纹夹角γ取15°~90°的裂尖SIFs,并与ANSYS计算结果进行对比,如图8所示,最大相对误差不超过3 %,计算结果非常吻合,进一步验证了本文方法具有较高的计算精度。由结果分析得,对于不同的裂纹夹角γ,KI,A、KI,B大小相等,符号相同,KII,A、KII,B大小相等,符号相反。由于裂尖奇异区相对位置随着裂纹夹角γ的变化而变化,取不同裂纹夹角γ与裂尖奇异区尺寸,研究其对裂尖SIFs的影响,本文方法计算结果如图9所示,裂尖SIFs随着裂纹夹角γ的变化而变化,但奇异区尺寸对裂尖SIFs几乎无影响,即采用本文方法计算斜十字裂纹各裂尖SIFs时,计算结果对奇异区尺寸不敏感。

图8 各裂尖SIFs与γ的关系
Fig.8 Relationship between SIFs andγ

图9 各裂尖SIFs与l/2的关系
Fig.9 Relationship between SIFs andl/2
4 结论
本文建立了交叉裂纹各裂尖SIFs同时快速求解的W单元,以十字交叉裂纹为例,根据裂纹的相对位置,分别对正交十字裂纹或斜十字裂纹裂尖SIFs相关参数进行了敏感性分析。虽然交叉裂纹各裂尖SIFs之间存在相互影响,不再相互独立,但采用本文方法分析交叉裂纹各裂尖SIFs发现其计算结果对裂尖奇异区尺寸等相关参数并不敏感,裂尖仍可按相互独立的关系来分析,证明了W单元分析交叉裂纹时仍具有高精高效性。算例分析表明:
① 对于等长正交十字裂纹问题,当板宽与裂纹长度满足W/a≥13时,可忽略板的尺寸效应,将模型当作无限大板进行计算,且荷载参数λ对无限大板界限没有影响;荷载参数λ和裂尖SIFs成线性变化规律,随着荷载参数λ的逐渐增大,KI,A逐渐减小,KI,B逐渐增大。
② 对于非等长正交十字裂纹问题,根据应力强度因子手册求解各裂尖SIFs时,相应修正系数可根据式(22)取值,从而简化计算并得到较高精度的SIFs解。
③ 对于斜十字裂纹问题,当裂纹夹角γ=45°时,若水平裂纹长度a保持不变,随着斜裂纹长度参数d的增加,KI,A、KII,C和KI,D逐渐减小,而KII,A、KI,B、KII,B和KI,C逐渐增大,KII,D则出现先减后增的趋势;应力强度因子手册中,对该模型C、D裂尖的II型SIFs系数错误,二者相互调换后可得到正确结果。当斜裂纹长度参数d=0时,取不同裂纹夹角γ,KI,A、KI,B大小相等,符号相同,KII,A、KII,B大小相等,符号相反。随着裂纹夹角γ的变化,各裂尖奇异区相对位置也随之改变,当裂尖奇异区尺寸改变时,对各裂尖SIFs几乎无影响,表明采用本文方法分析交叉裂纹问题时,各裂尖SIFs对奇异区尺寸不敏感。
